(笔记整合)二分法查找

一、什么是二分查找？

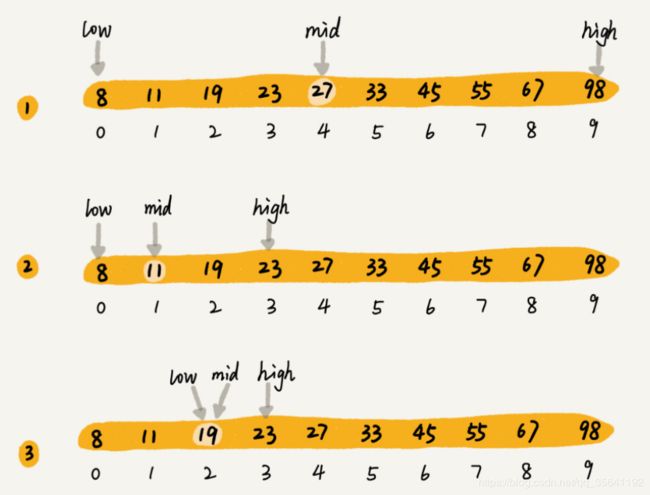
二分查找针对的是一个有序的数据集合，每次通过跟区间中间的元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间缩小为0。

二、时间复杂度分析？

1.时间复杂度
假设数据大小是n，每次查找后数据都会缩小为原来的一半，最坏的情况下，直到查找区间被缩小为空，才停止。所以，每次查找的数据大小是：n，n/2，n/4，…，n/(2^k)，…，这是一个等比数列。当n/(2^k)=1时，k的值就是总共缩小的次数，也是查找的总次数。而每次缩小操作只涉及两个数据的大小比较，所以，经过k次区间缩小操作，时间复杂度就是O(k)。通过n/(2^k)=1，可求得k=log2n，所以时间复杂度是O(logn)。

2.认识O(logn)
①这是一种极其高效的时间复杂度，有时甚至比O(1)的算法还要高效。为什么？
②因为logn是一个非常“恐怖“的数量级，即便n非常大，对应的logn也很小。比如n等于2的32次方，也就是42亿，而logn才32。
③由此可见，O(logn)有时就是比O(1000)，O(10000)快很多。

三、如何实现二分查找？

1.循环实现
代码实现：

    public int binarySearch1(int[] a, int val) {
        int start = 0;
        int end = a.length - 1;
        while (start <= end) {
            int mid = start + (end - start) / 2;
            if (a[mid] > val) {
                end = mid - 1;
            } else if (a[mid] < val) {
                start = mid + 1;
            } else {
                return mid;
            }
        }
        return -1;
    }

注意事项：
①循环退出条件是：start<=end，而不是start ②mid的取值，使用mid=start + (end - start) / 2，而不用mid=(start + end) / 2，因为如果start和end比较大的话，求和可能会发生int类型的值超出最大范围。为了把性能优化到极致，可以将除以2转换成位运算，即start + ((end - start) >> 1)，因为相比除法运算来说，计算机处理位运算要快得多。
③start和end的更新：start = mid - 1，end = mid + 1，若直接写成start = mid，end = mid，就可能会发生死循环。

2.递归实现

	public int binarySearch(int[] a, int val) {
        return bSear(a, val, 0, a.length - 1);
    }

    private int bSear(int[] a, int val, int start, int end) {
        if (start > end) { return -1; }
        int mid = start + (end - start) / 2;
        if (a[mid] == val) {
            return mid;
        } else if (a[mid] > val) {
            end = mid - 1;
        } else {
            start = mid + 1;
        }
        return bSear(a, val, start, end);
    }

四、使用条件（应用场景的局限性）

1.二分查找依赖的是顺序表结构，即数组。
2.二分查找针对的是有序数据，因此只能用在插入、删除操作不频繁，一次排序多次查找的场景中。
3.数据量太小不适合二分查找，与直接遍历相比效率提升不明显。但有一个例外，就是数据之间的比较操作非常费时，比如数组中存储的都是长度超过300的字符串，那这是还是尽量减少比较操作使用二分查找吧。
4.数据量太大也不是适合用二分查找，因为数组需要连续的空间，若数据量太大，往往找不到存储如此大规模数据的连续内存空间。

五、四种常见的二分查找变形问题

“十个二分九个错”。二分查找虽然原理极其简单，但是想要写出没有 Bug 的二分查找并不容易。
1.查找第一个值等于给定值的元素
2.查找最后一个值等于给定值的元素
3.查找第一个大于等于给定值的元素
4.查找最后一个小于等于给定值的元素

public class BinarySearch2 {
    public int bsearch1(int[] a, int value) {
        int low = 0;
        int high = a.length - 1;
        while (low <= high) {
            int mid = low + ((high - low) >> 1);
            if (a[mid] > value) {
                high = mid - 1;
            } else if (a[mid] < value) {
                low = mid + 1;
            } else {
                if ((mid == 0) || (a[mid - 1] != value)) {
                    return mid;
                } else {
                    high = mid - 1;
                }
            }
        }
        return -1;
    }

    public int bsearch2(int[] a, int value) {
        int low = 0;
        int high = a.length - 1;
        while (low <= high) {
            int mid = low + ((high - low) >> 1);
            if (a[mid] > value) {
                high = mid - 1;
            } else if (a[mid] < value) {
                low = mid + 1;
            } else {
                if ((mid == a.length - 1) || (a[mid + 1] != value)) {
                    return mid;
                } else {
                    low = mid + 1;
                }
            }
        }
        return -1;
    }

    public int bsearch3(int[] a, int value) {
        int low = 0;
        int high = a.length - 1;
        while (low <= high) {
            int mid = low + ((high - low) >> 1);
            if (a[mid] >= value) {
                if ((mid == 0) || (a[mid - 1] < value)) {
                    return mid;
                } else {
                    high = mid - 1;
                }
            } else {
                low = mid + 1;
            }
        }
        return -1;
    }

    public int bsearch4(int[] a, int value) {
        int low = 0;
        int high = a.length - 1;
        while (low <= high) {
            int mid = low + ((high - low) >> 1);
            if (a[mid] > value) {
                high = mid - low;
            } else {
                if ((mid == a.length - 1) || (a[mid + 1] > value)) {
                    return mid;
                } else {
                    low = mid + 1;
                }
            }
        }
        return -1;
    }
}

六、适用性分析

1.凡事能用二分查找解决的，绝大部分我们更倾向于用散列表或者二叉查找树，即便二分查找在内存上更节省，但是毕竟内存如此紧缺的情况并不多。
2.求“值等于给定值”的二分查找确实不怎么用到，二分查找更适合用在”近似“查找问题上。比如上面讲几种变体。

七、思考

如何在 1000 万个整数中快速查找某个整数？
这个问题并不难。我们的内存限制是 100MB，每个数据大小是 8 字节，最简单的办法就是将数据存储在数组中，内存占用差不多是 80MB，符合内存的限制。我们可以先对这 1000 万数据从小到大排序，然后再利用二分查找算法，就可以快速地查找想要的数据了。

看起来这个问题并不难，很轻松就能解决。实际上，它暗藏了“玄机”。如果你对数据结构和算法有一定了解，知道散列表、二叉树这些支持快速查找的动态数据结构。你可能会觉得，用散列表和二叉树也可以解决这个问题。实际上是不行的。

虽然大部分情况下，用二分查找可以解决的问题，用散列表、二叉树都可以解决。但是，不管是散列表还是二叉树，都会需要比较多的额外的内存空间。如果用散列表或者二叉树来存储这 1000 万的数据，用 100MB 的内存肯定是存不下的。而二分查找底层依赖的是数组，除了数据本身之外，不需要额外存储其他信息，是最省内存空间的存储方式，所以刚好能在限定的内存大小下解决这个问题。