树状数组详解！（C++_单点/区间查询_单点/区间修改）

先把这张著名的树状数组结构图摆在最前面，接下来我们就以这张图讲起！

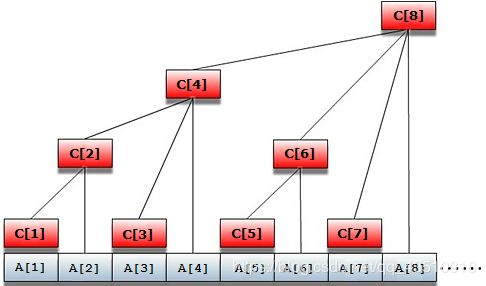
       首先图中的A数组就是所谓的原数组，也就是普通的数组形态，C则是我们今天要说的树状数组（可以看出一个树的形状，但其实和树没多大关系）
从图中可以明显看到以下几个式子：
$C[1]=A[1];$
$C[2]=C[1]+A[2]=A[1]+A[2];$
$C[3]=A[3];$
$C[4]=C[2]+C[3]+A[4]=A[1]+A[2]+A[3]+A[4];$
$C[5]=A[5];$
$C[6]=C[5]+A[6]=A[5]+A[6];$
$C[7]=A[7];$
$C[8]=C[4]+C[6]+C[7]+A[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];$
有点像前缀和不是？
但这样还看不出什么整体规律，所以我们再来变一下，把十进制编程变成二进制：
$C[0001]=A[0001];$
$C[0010]=A[0001]+A[0010];$
$C[0011]=A[0011];$
$C[0100]=A[0001]+A[0010]+A[0011]+A[0100];$
$C[0101]=A[0101];$
$C[0110]=A[0101]+A[0110];$
$C[0111]=A[0111];$
$C[1000]=A[0001]+A[0010]+A[0011]+A[0100]+A[0101]+A[0110]+A[0111]+A[1000];$
这下有没有找到规律呢？
注意观察C数组的二进制的最低位的1的位置。你会发现：将每一个二进制，去掉所有高位1，只留下最低位的1，然后从那个数一直加到1。
在程序中如何实现去掉所有高位的1呢?

int lowbit(int x){
    return x & -x;
}

lowbit()函数一知半解请的看这里：

负数的补码等于原码加一，正数的补码和原码相等。运用这个特性，将两者进行与运算就能知道第一个1的位置了，还是不懂的可以看这个栗子：
6的原码：0110； 6的补码：0110；
-6的反码：1001；（反码等于原码置反）
-6的补码：1010；（补码等于反码加一） （6的补码）&（-6的补码）=0110&1010=0010； 这样就只剩下最低为的1了！

下来正式解释几个常用的树状数组函数：

1.单点修改

void add(int x, int k)
{
    while (x <= n)
    {
        tree[x] += k;
        x += lowbit(x);
    }
}

因为树状数组是牵一发而动全身，所以一直lowbit即可，这个过程正是我之前所模拟的算式。你想啊要是A[1]要加k, 那么是不是后面要用到A[1]的都得加k！就是这个理！

2.区间查询

就是前缀和，比如查询x到y区间的和，那么就将从1到y的和减去从1到x的和。

从1到y的和求法是，将y转为2进制，然后一直减去lowbit(y)，一直到0

比如求1到7的和（配合开始那张图理解效果更佳！）
$ans+=c[0111];$
$ans+=c[0111-0001(0110)];$
$ans+=c[0110-0010(0100)];$
$ans+=c[0100-0100(c[0]无意义，结束)]$

int sum(int x)
{
    int ans=0;
    while(x!=0)
    {
        ans+=tree[x];
        x-=lowbit(x);
    }
    return ans;
}

3.区间修改&&单点查询

先给代码：

void add(int x, int k)//你没有看错，我和单点修改的代码是一样的！（主函数操作要变，请看下面解释！）
{
    while (x <= n)
    {
        tree[x] += k;
        x += lowbit(x);
    }
}

详细：
       假设我们要修改[x， y]这个区间的数，我们想给这个区间所有的数都加k！那我们是不是可以给从x到n的所有数都加上k, 再给从y+1到n的所有数加上-k！

实际主函数中的操作：

            add(x, k);
            add(y + 1, -k);

       你有没有发现其实这里有个很神奇的设定：在实际操作中其实并没有给$x$到$y$的所有数都加$k$,只是给$C[x]$加了$k$（当然后面与$C[x]$有关的也要改），然后再给$C[y-1]$加了$-k$（当然后面与C[y-1]有关的也要变），为什么会这样设定呢？按照常规思维的话这样操作会导致中间有的数未加上$k$，但是存在即合理！因为你要输出的时候是不是要引用$sum$函数？$sum$函数是不是会加上之前所有的数？那$x$和$y$之间的数是不是最终还是会加上x位置的那个$k$！！！
       但是这个时候就又发现了一个问题，我想要单点查询怎么办？比如查询x+3这个位置上的数（$x<(x+3)<y$），按照之前区间查询的思想$sum(x)-sum(x-1)$，那之前操作中要加上去的$k$怎么办？？？蛤！所以这里的树状数组就不能加上原数组中的数了，直接在初始时将树状数组全部置零，树状数组中只保存区间修改所操作的值$k$，这样就可以明目张胆的使用$sum()$了，直接从$C[x-3]$加到$C[1]$，反正又不会加到多余的数，毕竟原数组和树状数组没关系了嘛，只需要在输出的时候多加上一个原数组的当前的值就好！

比如像这样：

  cout << A[x+3] + sum(x+3) << endl;

所以单点查询的代码和区间查询也是一样的，只不过是主函数中的操作稍微变了下~
下面我贴两个模板题，有兴趣的话可以去康康：

P3374 【模板】树状数组 1
（单点修改+区间查询）

Code

#include
using namespace std;
int tree[500010];
int n, m;
int lowbit(int x)
{
    return x & -x;
}
void add(int x, int k)
{
    while (x <= n)
    {
        tree[x] += k;
        x += lowbit(x);
    }
}
int sum(int x)
{
    int ans = 0;
    while (x != 0)
    {
        ans += tree[x];
        x -= lowbit(x);
    }
    return ans;
}
int main()
{

    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        int a;
        cin >> a;
        add(i, a);
    }
    for (int i = 1; i <= m; i++)
    {
        int u, v, w;
        cin >> u >> v >> w;
        if (u == 1)
            add(v, w);
        else if (u == 2)
            cout << sum(w) - sum(v - 1) << endl;
    }
    return 0;
}

P3368 【模板】树状数组 2
（区间修改+单点查询）

Code

#include
using namespace std;
int tree[500010], y[500010];
int n, m;
int lowbit(int x)
{
    return x & -x;
}
void add(int x, int k)
{
    while (x <= n)
    {
        tree[x] += k;
        x += lowbit(x);
    }
}
int sum(int x)
{
    int ans = 0;
    while (x != 0)
    {
        ans += tree[x];
        x -= lowbit(x);
    }
    return ans;
}
int main()
{

    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> y[i];
    for (int i = 1; i <= m; i++)
    {
        int u, a, b, c, v;
        cin >> u;
        if (u == 1)
        {
            cin >> a >> b >> c;
            add(a, c);
            add(b + 1, -c);
        }
        else if (u == 2)
        {
            cin >> v;
            cout << y[v] + sum(v) << endl;
        }
    }
    return 0;
}