SDUWH 新星赛线上模拟赛

7-1 factorial
题目描述
In many applications very large integers numbers are required. Some of these applications are using keys for secure transmission of data, encryption, etc. In this problem you are given a number, you have to determine the number of digits in the factorial of the number.
输入格式:
Input consists of several lines of integer numbers. The first line contains an integer T, which is the number of cases to be tested, followed by T lines, one integer 1 ≤ n ≤ 10000000 on each line.

1≤T≤10
输出格式:
The output contains the number of digits in the factorial of the integers appearing in the input.
输入样例:
2
10
20

输出样例:
7
19
Solution

求n！的位数。
即求log10(n!)
log10(n!) =log10(n * (n - 1) * … * 1) = log10(n) + … + log10(1）
求出结果下取整加一即为答案。

代码

#include
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int SZ = 100000 + 10; 
int n;
double ans;
int main()
{
	int T; 
	scanf("%d",&T);
	while(T -- )
	{
		scanf("%d",&n);
		ans = 0;
		for(int i = 1;i <= n;i ++ ) ans += log10(i);
		printf("%lld\n",(ll)(ans)+ 1);
	}
	return 0;
}

7-2 exam
题目描述
The final exam is over. In order to give rewards, the teacher should rank the students in the class.

There are N students in the class. This semester, they have learned K courses.

The student number of the i-th student is Xi, and his score of the j-th course is expressed as Aij.

The ranking rules are as follows:

If the scores of two students are different, the first course with different scores will be the basis for ranking, and the one with higher scores will come first.

If the scores of the two students are identical, the one with the smaller student number will come first.
输入格式:
The first line contains N, K (N≤1000,K≤10).

In the following N lines, the i-th line contains K+1 integers X​i A​i1 A​i2 A​i3… A​ik. (X​i <100000,A​ij<100000)
Guarantee student number is different.
输出格式:
A line contains n integers, which are the student numbers from the first to the last, separated by spaces.
There should be a space after the last number.
输入样例:
4 3
1 1 2 3
2 1 3 3
3 2 2 2
4 2 2 3
输出样例:
4 3 2 1
Solution

按关键字排序即可。

代码

#include
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int SZ = 1000 + 10; 
struct zt	
{
	int id;
	int ke[20];
}peo[SZ];
int n,k;
bool cmp(zt a,zt b)
{
	for(int i = 1;i <= k;i ++ )
	if(a.ke[i] != b.ke[i]) return a.ke[i] > b.ke[i];
	return a.id < b.id;
}
int main()
{
	scanf("%d%d",&n,&k);
	for(int i = 1;i <= n;i ++ )
	{
		scanf("%d",&peo[i].id);
		for(int j = 1;j <= k;j ++ )
		{
			scanf("%d",&peo[i].ke[j]);
		}
	}
	sort(peo + 1,peo +n+1,cmp);
	for(int i = 1;i <= n;i ++ )
	{
		printf("%d ",peo[i].id);
	}
	return 0;
}

7-3 stack
题目描述
Xiaoming is learning stack. Stack is a last in, first out data structure. There are only two operations: adding an element to the end of the stack and taking out the end element. Now Xiaoming asks you to help him simulate the operation of the stack.
输入格式:
The first line contains an integer n indicating how many operations there are. (N≤100000)

Next N lines, two integers A and B per line. A = 1 means to add B to the tail of the stack, A = 2 means to take out the tail element of B times. (B<100000)

The stack is initially empty. Ensure that elements are not removed from the empty stack.
输出格式:
The first line, an integer m, indicates how many elements are left in the stack.
The second line, m integers, lists the m elements from the beginning to the end of the stack, separated by spaces.
输入样例:
5
1 2
1 4
2 1
1 3
1 5
5 1 2
输出样例:
3
2 3 5
Solution

模拟栈。

代码

#include
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int SZ = 1000 + 10; 
int ans[100005],temp;
stack<int> q;
int main()
{
	int n;
	scanf("%d",&n);
	while(n -- )
	{
		int a,b;
		temp = 0;
		scanf("%d%d",&a,&b);
		if(a == 1)
		{
			q.push(b);
		}
		else if(a == 2)
		{
			for(int i = 1;i <= b;i ++)
			q.pop();
		}
	} 
	while(!q.empty())
	{
		ans[++temp] = q.top(); 
		q.pop();
	} 
	printf("%d\n",temp);
	for(int i = temp;i >= 1;i -- )
	{
		printf("%d ",ans[i]);
	}
	return 0;
}

7-4 Hateful fat
题目描述
LCY lost his pen when he was studying, which is really a bad situation, because his eyes have been blocked by his fat. So can you tell him the positional relationship between him and the pencil?

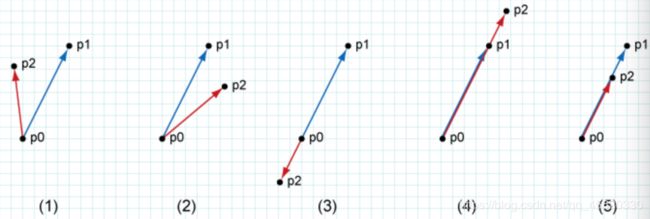
For given three points p0,p1,p2,

print " COUNTER_CLOCKWISE” if p0,p1,p2 make a counterclockwise turn (1)

print " CLOCKWISE” if p0,p1,p2 make a clockwise turn (2),

print " ONLINE_BACK” if p2 is on a line p2,p0,p1 in this order (3),

print " ONLINE_FRONT “if p2 is on a line p0,p1,p2 in this order (4),

print " ON_SEGMENT” if p2 is on a segment p0p1(5).
Input:
In the first line, integer coordinates of p0 and p1 are given.

The next line gives an integer q, which represents the number of queries.

Then, q queries are given for integer coordinates of p2.
Output:
For each query, print the above mentioned status.
Sample Input:
0 0 2 0
3
-1 1
-1 -1
2 0
Sample Output:
COUNTER_CLOCKWISE
CLOCKWISE
ON_SEGMENT

Solution

判断点与线段的关系。
用向量判断。
（a,b）与（c，d）的关系 :
a * d == b * c 平行 -> 再判断同向与反向 和 长度比较
b * c > a * d 在左侧
b * c < a * d 在右侧
代码

#include
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
ll n,x,y,z,w,p,q;
ll xx,yy,zz,ww,pp,qq;
int main()
{
	while(scanf("%lld%lld%lld%lld",&x,&y,&z,&w) == 4)
	{
		scanf("%lld",&n);
		xx = z - x;
		yy = w - y;
		for(int i = 1;i <= n;i ++)
		{
			scanf("%lld%lld",&p,&q);
			zz = p - x;
			ww = q - y;
			if(xx * ww == yy * zz )
			{
				if(zz * xx < 0 || ww *yy < 0) printf("ONLINE_BACK\n");
				else 
				if(zz * zz +ww * ww > xx * xx + yy * yy) printf("ONLINE_FRONT\n");
				else printf("ON_SEGMENT\n");
			}
			else 
			{
				if(zz * yy > ww * xx) printf("CLOCKWISE\n");
				else  printf("COUNTER_CLOCKWISE\n");
			}	
		}
	}
	return 0;
} 

7-5 prime
题目描述
Xiaoming is learning prime number, which is a integer greater than 1 and can only be divided by 1 and itself. Xiao Ming has learned how to judge whether a number is prime. Now, he wants to know how many prime numbers are in [1, N].
输入格式:
An integer N.(N<=10000000)
输出格式:
An integer represents how many prime numbers are in [1, N].
输入样例:
10
输出样例:
4
Solution
找素数个数。
O（n）欧拉筛。
代码

#include
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int SZ = 10000000 + 10; 
int prime[SZ],p[SZ],tot;
int main()
{
	int n,ans = 0;
	scanf("%d",&n);
	for(int i = 2;i <= n;i ++ )	
	{
		if(prime[i] == 0) 
			p[ ++ tot] = i;
		for(int j = 1;j <= tot && i * p[j] <= n;j ++ )
		{
			prime[i * p[j]] = 1;
			if(i % p[j] == 0) break;
		}
	}
	for(int i = 2;i <= n;i ++)
	if(!prime[i]) ans ++ ;
	printf("%d",ans);
	return 0;
}

7-6 lcy‘s weight
题目描述
During the holiday, LCY has been eating snacks, but sometimes he also exercises, so his weight has been changing. At the same time, LCY is an excellent college student, so he records the change of his weight the day before every day. But n days later, he found that he could not know how heavy he was now, but he could remember his weight on the first day as M. So LCY found smart you. I hope you can help him calculate his weight now, so can you help him?

Input:
The first line gives two integers, N and M, representing the days lcy experienced and the weight of the first day.(n≤10^​4)
(m≤10^10000 )
Then n lines followed.
Each line contains two integers x and y.(y≤10^​10000)
When x equals 1, it means that LCY’s current weight is y heavier than the previous day.
When x equals 2, it means that LCY’s current weight is y lighter than the previous day.
When x equals 3, it means that LCY’s current weight is y times heavier than the previous day.
Ensure LCY’s weight is always less than 10^​10000
Output:
Output a single line represents the weight after n days of LCY
Input Sample:
4 70
1 3
3 10
2 100
3 10000000000
Output Sample:
6300000000000
Solution

java大数

代码

import java.math.*;
import java.util.*;
public class Main {
    public static void main(String[] args)
    {
        Scanner cin = new Scanner(System.in);
        int n = cin.nextInt();
        int k;
        BigInteger m = cin.nextBigInteger();
        for(int ii = 1;ii <= n;ii ++ )
        {
            BigInteger a;
            k = cin.nextInt();
            a = cin.nextBigInteger();
            if(k == 1)
                m = m.add(a);
            else if(k == 2)
                m = m.subtract(a);
            else if(k == 3)
                m = m.multiply(a);
        }
        System.out.println(m);
    }
}

7-7 Prepare for CET-6

题目描述
In order to prepare the CET-6 exam, LCY is reciting English words recently. Because he is already very clever, he can only recite n words to get full marks. He is going to memorize K words every day. But he found that if the length of the longest prefix shared by all the strings in that day is a​i, then he could get a​i laziness value. The lazy LCY must hope that the lazier the better, so what is the maximum laziness value he can get?
For example:
The group {RAINBOW, RANK, RANDOM, RANK} has a laziness value of 2 (the longest prefix is ‘RA’).
The group {FIRE, FIREBALL, FIREFIGHTER} has a laziness value of 4 (the longest prefix is ‘FIRE’).
The group {ALLOCATION, PLATE, WORKOUT, BUNDLING} has a laziness value of 0 (the longest prefix is ‘’).
Input:
The first line of the input gives the number of test cases, T. T test cases follow. Each test case begins with a line containing the two integers N and K. Then, N lines follow, each containing one of Pip’s strings.
2≤N≤10^​5
2≤K≤N
Each of Pip’s strings contain at least one character.
Each string consists only of letters from A to Z.
K divides N.
The total number of characters in Pip’s strings across all test cases is at most .
Output:
For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is the maximum sum of scores possible.

Input sample:
2
2 2
KICK
START
8 2
G
G
GO
GO
GOO
GOO
GOOO
GOOO

Output Sample:
Case #1: 0
Case #2: 10

Solution
将n个字符串每k个一组进行分组，求每组的最长公共前缀之和的最大值。

字典树 + 贪心。

先从最深的字符判断是否满足有k个，贡献最大的公共前缀，依次往上层递归。

代码

#include
using namespace std;
typedef long long ll;
const int SZ = 2e6 + 100;
int cnt,sum[SZ],temp,n,k;
struct node
{
	int nxt[30]; 
}trie[SZ];

inline void add(string s)
{
	int root = 1;
	for(int i = 0;i < s.size();i ++ )
	{
		if(trie[root].nxt[s[i] - 'A'])
			root = trie[root].nxt[s[i] - 'A'];
		else 
		{
			trie[root].nxt[s[i] - 'A'] = ++ cnt;
			root = cnt;
		}
		sum[root] ++ ;
	} 
}

int main()
{
	int T;
	string s;
	scanf("%d",&T);
	while(T -- )
	{
		memset(trie,0,sizeof(trie));
		memset(sum,0,sizeof(sum));
		cnt = 1;
		scanf("%d%d",&n,&k);
		for(int i = 1;i <= n;i ++ )
		{
			cin >> s;
			add(s);
		}
		int ans = 0;
		for(int i = 1;i <= cnt;i ++ )
		{
			ans += (sum[i]/k);
		}
		printf("Case #%d: %d\n",++temp,ans);
	}
	return 0;
} 

7-8 Computer Games

题目描述
LCY is playing games with his computer at home. Each playing card has two attributes: A​i and B​i, LCY and his computer take turns selecting playing cards,with LCY going first. In each turn, a player can select one card, as long as that playing card either has an A​i greater than each of the all soldiers selected so far, or has a B​i greater than each of the all cards selected so far.
To be precise: let A​i and B​i be the values for the i-th cards, for i from 1 to N, and let S be the set of cards that have been selected so far. Then a player can select card x if and only if at least one of the following is true:
Ax >A​s for all s in S
B​x >B​s for all s in S
If no selection can be made, then the selection process ends and the player with more playing cards win. LCY wants to select more cards and win the game. If both players play optimally to accomplish their goals, can LCY succeed?
输入格式:
The first line of each case contains a positive integer N, the number of cards. N more lines follow; the i-th of these line contains two integers Ai and Bi, indicating the values of the i-th cards.(N≤4000,0≤A​i,B​i≤10000)
输出格式:
For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is YES or NO, indicating whether LCY can guarantee that he selects more cards than computer, even if computer plays optimally to prevent this.

Input Sample:
3
3
10 2
1 10
10 3
3
10 1
10 10
1 10
3
10 2
1 10
4 9

Output Sample:
Case #1: NO
Case #2: YES
Case #3: YES

Solution

博弈

将每个Ai和Bi当作坐标画在坐标系上，每选择一个点，都会导致它下方的点和它左侧的点都不可以选取。这样如果出现Ai和Bi的最大值不在同一点上，先手必败，故想一种策略可以使得转换先手后手。即寻找一个同时在Ai最大值的点和Bi最大值的点的左下方的点（且该点为当前区间A，B均最大的点），取这个点即可转换先手与后手。若在左下这个区间又出现相同情况，则继续缩小区间，看看这个区间是否有Ai，Bi均最大的点来转换，若存在则可取胜，不存在则失败。

代码

#include
using namespace std;
const int SZ = 40000 + 20;
int a[SZ],b[SZ]; 
int n,cnt;
inline bool check()
{
	int tot = n;
	int topa = 1e4 + 10,topb = 1e4 + 10;	
	while(tot -- )
	{
		int nowa = 0,nowb = 0;
		for(int i = 1;i <= n;i ++ )
		{
			if(a[i] < topa && b[i] < topb)
			{
				nowa = max(nowa,a[i]);
				nowb = max(nowb,b[i]);
			}
		}
		for(int i = 1;i <= n;i ++ )
		{
			if(a[i] == nowa && b[i] == nowb)
			{
				return 1;
			}
		}
		topa = nowa,topb = nowb;
	}
	return 0;
}
int main()
{
	int T;
	scanf("%d",&T);
	while(T -- )
	{
		scanf("%d",&n); 
		for(int i = 1;i <= n;i ++ ) scanf("%d%d",&a[i],&b[i]);
		int flag = check();
		if(flag == 1) printf("Case #%d: YES\n",++cnt);
		else printf("Case #%d: NO\n",++cnt);
	}
}

7-9 sort
题目描述
Xiaoming is tired of asking for help. This time he wants to test you.

He gave you N integers. Please find the number with the largest M.

输入格式:
The first row has two numbers N, M (0

The second line contains N integers that are different and are all in the interval [- 500000,500000].

输出格式:
Output the number of the first M in the order of large to small.

输入样例:
5 3
3 -35 92 213 -644

输出样例:
213 92 3

Solution

排序

代码

#include
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int SZ = 1000000 + 10;
int num[SZ];
bool cmp(int a,int b)
{
	return a > b;
} 
int main()
{
	int n,m,x;
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i ++ )
	scanf("%d",&num[i]);
	sort(num + 1,num +n + 1,cmp);
	for(int i = 1;i <= m;i ++ )
	printf("%d ",num[i]);
	return 0;
}

7-10 lcy eats biscuits
题目描述
In order to grow nine abdominal muscles, LCY began to eat all the N biscuits in his room, but LCY didn’t like walking, because walking would cause his abdominal muscles to become smaller.How long does he have to run to get n biscuits. At the beginning, LCY is at (0,0)

Input:
The first line is a positive integer N.(N≤14)

Next, there are 2 real numbers in each line, representing the coordinates of the ith biscuits.(−10000≤xi,y​i ≤10000)
The distance formula between two points is√​(x1−x2) ^ 2 + (y1−y2) ^ 2

Output:
A number, representing the minimum distance to run, with 2 decimal places reserved.

Input Sample:
4
1 1
1 -1
-1 1
-1 -1

Output Sample:
7.41

Solution

NP问题
n <= 14 : dfs + 剪枝
n <= 20 : 状压dp

代码

#include
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
int a[120],b[120],m;
double t[120][120];
double ans = INF ;
bool vis[120]; 

void dfs(int x,double tot,int ha)
{
	if(ha > 0 && tot >= ans) return; //剪枝
	if(ha == 0) 
	{
		ans = min(tot,ans);
	}
	for(int i = 1;i <= m;i ++ )
	{
		if(!vis[i] && i != x)
		{
			vis[i] = 1;
			dfs(i,tot + t[x][i],ha - 1);
			vis[i] = 0;
		}
	}
}
int main()
{
	scanf("%d",&m);
	for(int i = 1;i <= m;i++) 
	scanf("%d%d",&a[i],&b[i]);
	a[0] = 0;
	b[0] = 0;
	for(int i = 0;i <= m;i  ++ )
	for(int j = 0;j <= i;j ++ )
	{
		t[i][j] = sqrt((a[i] - a[j]) * (a[i] - a[j]) + (b[i] - b[j]) *(b[i] - b[j]));
		t[j][i] = sqrt((a[i] - a[j]) * (a[i] - a[j]) + (b[i] - b[j]) *(b[i] - b[j]));
	}
	dfs(0,0,m);
	printf("%.2lf",ans);
	return 0;
} 

2020.4.1