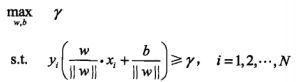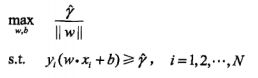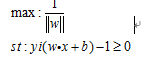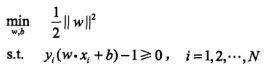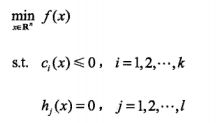SVM数学基础的学习
今天，使用《统计学习方法》来简单学习一下SVM的数学基础，为了编写第一个行人识别的程序做基础
1、超平面是什么？
超平面就是直线在多维空间的延伸，n维空间的超平面是n-1维的
2、线性可分：超平面可以把两类样本完全的分割开来
3、特征点到超平面的几何距离：
其中r为特征向量x到超平面的几何距离，g（x）是超平面的函数距离
4、间隔最大化的理解
间隔最大化超平面求解问题最终转换成了以下的最优化的问题：
（1）
转化为函数间隔的表达式为：
（2）
《统计学习方法》举了一个例子，对w和b等比例缩放y也等比例缩放对超平面的求解没有影响，这是因为超平面
和（w*x+b）是等价的一次该约束条件可以进一步转化为：（一篇博文的解释如下：
我们的目的是最大化支持向量到分割超平面的几何间隔r，而不是最大化函数间隔g(x)，为什么呢？因为超平面方程的系数可以同比例增大或者减小，而不改变超平面本身。所以||w0||是不固定的，这就会影响函数间隔g(x)的大小。
所以我们需要最大化的是几何间隔r，这等价于我们固定||w0||，然后最大化函数间隔g(x)。但是实际上我们不会这么做，通常的处理方法是固定函数间隔g(x)的绝对值为1，然后最小化||w0||。也就是说我们把支持向量到分割超平面的函数间隔g(x)的绝对值设定为1，然后最小化||w0||
）
（3） →→ 
（4）
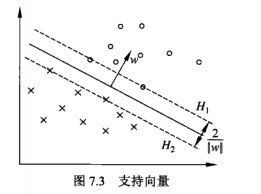
（3）式中max可以理解为距离超平面最近的点与超平面的间隔最大化，如下图所示中这些离超平面最近的点就是我们所说的支持向量，由此可以看出超平面的确定只是与支持向量有关的，从（1）式中我们可以理解为，数据集中的特征点到超平面的距离必须大于最大化间隔
5、为什么引入对偶问题？
5.1、首先对于等式的约束条件下，求解函数的最小值，可以值求导。而约束条件为不等式的时候，求解过程会变得复杂，为了使问题变得易于处理，我们的方法是把目标函数和约束全部融入一个新的函数，即拉格朗日函数，在通过这个函数来寻找最优点。
5.2、考虑原始优化问题如下：
（1）
由上述原始问题构成拉格朗日函数
，定义以下等式：
（2），将（2）展开为：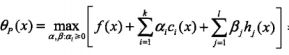
（3），当c与h不满足约束条件的时候我们可以令相应的α和β为+∞，这时的（3）公式的值为+∞，反而当c与h符合约束条件的时候，θp(x)=f(x),这时
，当x满足原始问题的约束的时候，就有min θp(x) 等价于原始问题（1），也就是说他和原始问题有同样的解。
由于拉格朗日函数的对偶性质，
是原始问题
的对偶问题，根据相关定理推论有，当原始问题的最优解与对偶问题最优解相等的时候p=d，且x，α，β分别为原始问题和对偶问题的可行解，则他们分别是原始问题和对偶问题的最优解（KTT条件就是上述结论的充分必要条件）。因此对对偶问题求解就可以等到原始问题的最优解。
反观对偶问题问题因为拉格朗日函数为凸函数，因此L(x,α,β)必然有最小值，而且先求最小值再求最大值相对于原始问题是方便的，首先求min L(x,α,β)对w，b分别求偏导得：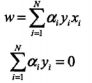
然后求极大max min L(x,α,β)有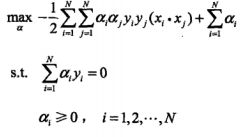
，然后件max转化为
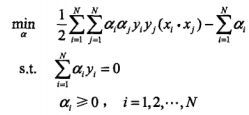，然后不等式问题就转化成了等式优化问题。（这就是为什么要转化为对偶问题的原因）
SVM与感知机的区别
6、关于SMO算法的问题参考以下博文：
http://www.cnblogs.com/liqizhou/archive/2012/05/11/2496029.html
总结摘自以上博文：
这份SVM的讲义重点概括了SVM的基本概念和基本推导，中规中矩却又让人醍醐灌顶。起初让我最头疼的是拉格朗日对偶和SMO，后来逐渐明白拉格朗日对偶的重要作用是将w的计算提前并消除w，使得优化函数变为拉格朗日乘子的单一参数优化问题。而SMO里面迭代公式的推导也着实让我花费了不少时间。
对比这么复杂的推导过程，SVM的思想确实那么简单。它不再像logistic回归一样企图去拟合样本点（中间加了一层sigmoid函数变换），而是就在样本中去找分隔线，为了评判哪条分界线更好，引入了几何间隔最大化的目标。
之后所有的推导都是去解决目标函数的最优化上了。在解决最优化的过程中，发现了w可以由特征向量内积来表示，进而发现了核函数，仅需要调整核函数就可以将特征进行低维到高维的变换，在低维上进行计算，实质结果表现在高维上。由于并不是所有的样本都可分，为了保证SVM的通用性，进行了软间隔的处理，导致的结果就是将优化问题变得更加复杂，然而惊奇的是松弛变量没有出现在最后的目标函数中。最后的优化求解问题，也被拉格朗日对偶和SMO算法化解，使SVM趋向于完美。
另外，其他很多议题如SVM背后的学习理论、参数选择问题、二值分类到多值分类等等还没有涉及到，以后有时间再学吧。其实朴素贝叶斯在分类二值分类问题时，如果使用对数比，那么也算作线性分类器。