ACM个人笔记
基本算法
- 1、枚举
- 2、模拟
- 3、二分
- 二分查找
- 二分答案+检验
- 4、并查集
- 5、DFS
- 6、BFS
- 7、DP
- 8、树状数组
- 9、线段树
- 10、最短路
- 11、最小生成树
- 12、素数
- 13、矩阵快速幂
- 14、网络流
- Dinic
- 有流量上下界的网络最大流
- 15、博弈
- Nim
- SG函数
- 16、欧几里得,中国剩余定理
- 扩展欧几里得
- 线性同余方程,中国剩余定理
- 17、其他数学定理
- 费马小定理
- 欧拉定理
1、枚举
从问题的所有可能解的集合中一一枚举,判断能使命题成立的解。
HDU5660
POJ1006
2、模拟
根据题意一步步走代码,通常会设坑。
POJ1298
POJ2632
POJ1922
POJ1068
3、二分
二分查找
在一个单调有序集合中查找元素,每次将集合分为左右两部分,判断解在哪个部分并调整上下界,直到找到目标。
k = (low+top)/2
array[k] == key -------succeed
array[k] > key ---------array[low ~ k-1]
array[k] < key ---------array[k+1 ~ top]
二分答案+检验
可以确定解在一个有序的范围内,用二分查找的方式查找正确的解。
每次判断都采用一个检验函数。
ZOJ4130
POJ2785
HihoCoder1139
HDU5038
POJ1018
4、并查集
初始化每个节点的父节点是自己
查询2个点是否在同一集合:比较最高父节点是否相同
合并:一个节点的最高父节点等于另一个节点
优化:使每个点的直接父节点是最高父节点
5、DFS
一条路走到黑,并标记走过的点,走不了就回退。
POJ2386
百练2815
百练4103
百练4123
POJ3083
POJ1321
6、BFS
一层一层的走。
POJ3278
百练4116
7、DP
将一个问题分解成许多子问题。
将问题转化为01背包
完全背包改一下初始化
//不压缩
for(int i=1;i<=m;i++)
for(int j=n;j>=w[i];j--)
dp[i][j] = max(dp[i-1][j] , dp[i-1][j-w[i]] + v[i]);
//滚动数组
for(int i=1;i<=m;i++)
{
int tap=i%2;
for(int j=n;j>=w[i];j--)
dp[tap][j] = max(dp[!tap][j] , dp[!tap][j-w[i]] + v[i])
}
//一维数组
for(int i=1;i<=m;i++)
for(int j=n;j>=w[i];j--)
dp[j] = max(dp[j] , dp[j-w[i]] + v[i])
POJ3624
POJ1276
HDU2546
HDU3449
HDU1284
HDU2191
HDU1024
树形DP
POJ2342
POJ1463
状压DP
HDU1074
8、树状数组
单点的快速更新
用于求前缀和->区间和
#define lowbit(i) (i&(-i))
void update(int x,int e)//将第x个数加e
{
while(x < n)
{
t[x] += e;
x += lowbit(x);
}
}
int sum(int k)//前k个数的和
{
int ans = 0;
while(k>0)
{
ans+=t[k];
k-=lowbit(k);
}
return ans;
}
POJ3468
HDU1166
POJ2352
POJ3321
POJ2182
9、线段树
线段树是一棵二叉树,树中的每一个结 点表示了一个区间[a,b]。a,b通常是整数。
每一个叶子节点表示了一个单位区间(长度为1)。
对于每一个非叶结点所表示的 结点[a,b],其左儿子表示的区间为 [a,(a+b)/2],右儿子表示的区间为 [(a+b)/2+1,b]。

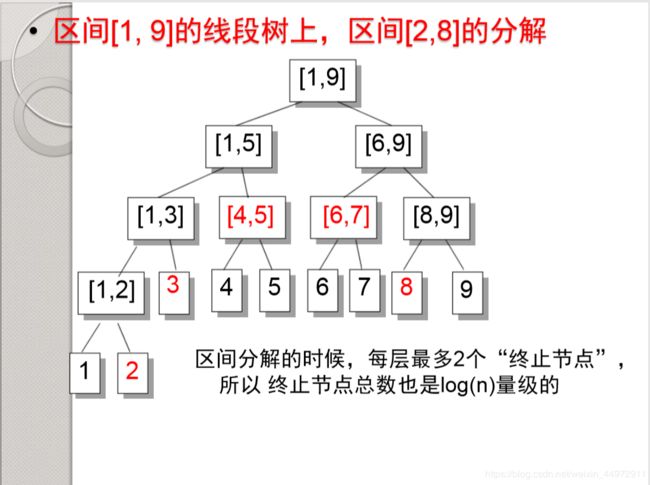
主要用于求区间最大值和最小值。
POJ3264
10、最短路
给定一张n个点m条边的正权有向图,求1号点到其他点的最短路径
按照最短路的大小从小到大加入队列,用优先队列进行维护
POJ2387
POJ1251
11、最小生成树
给定一张n个点的带权无向图,求权值最小的生成树
kruskal算法: 将边按照权值大小排序,之后能加就加,用并查集维护
prim算法: 按照点进行贪心
POJ2253
POJ1287
12、素数
埃筛
质数的倍数都不是质数
bool prime[N];
void init()
{
for(int i=2;iPOJ2689
13、矩阵快速幂
LL pow_mod(LL a,LL b, LL m)//a的b次方模m
{
LL ret = 1;
while(b)
{
if(b&1)ret = (ret * a)%m;//如果b是奇数
a = (a * a)%m;
b>>=1;//b除等于2
}
return ret;
}
把其中的乘法改为矩阵的乘法就行
HDU1757
HDU3483
HDU2866
POJ1995
14、网络流
给定一个有向图G=(V,E),把图中的边看作 管道,每条边上有一个权值,表示该管道 的流量上限。给定源点s和汇点t,现在假设 在s处有一个水源,t处有一个蓄水池,问从 s到t的最大水流量是多少 。
先dfs分层,然后取最小的路径,减去正向的边,添加反向边。
继续dfs,直到分层无法到达汇点
Dinic
分完层次后,从源点开始,用dfs从前一层向后一层反复寻找增广路。
DFS过程中,要是碰到了汇点,则说明找到了一条增广路径。此时要增加总流量的值,消减路径上各边的容 量,并添加反向边,即所谓的进行增广。
DFS找到一条增广路径后,并不立即结束,而是回溯后继续DFS寻找下一个增广路径。
回溯到最小边中最上层的起点。
如果回溯到源点而且无法继续往下走了,DFS结束。
求每条边的容量:
将原图备份,原图上的边的容量减去做完最大 流的残余网络上的边的剩余容量,就是边的流量。
int depth[N];
bool fenc(int s,int t)//以s为源点,t为汇点分层
{
memset(depth,-1,sizeof(depth));
depth[s]=0;
queue Q;
Q.push(s);//源点入队列
while(!Q.empty())
{
int v = Q.front();
Q.pop();
for(int i=1;i<=N;i++)
if(depth[i]==-1&&G[v][i]>0)//深度值未被改变说明未被访问
{
depth[i] = depth[v] + 1;
if(i == t)return true;//分层到汇点就行
else Q.push(i);
}
}
return false;
}
bool visit[N];
int Dicnic(int s,int t)
{
deque Q;
int sumedn = 0;
while(fenc(s,t))//只要能分层
{
Q.push_back(s);
meset(visit,0,sizeof(visit));
visit[s] = true;
while(!Q.empty())
{
int nd = Q.back();
if(nd == t)//如果nd 是汇点
{
int minline = 0xfffffff;//最小边
int minpoint;//最小边的起点
for(int i=1;iG[vs][vt])
{
minline = G[vs][vt];
minpoint = vs;
}
}
/*增广,改图*/
sumedn += minline;
for(int i=1;i0&&depth[nd]+1==depth[i])
//往下一层走
{
visit[i] = true;
Q.push_back(i);
break;
}
}
if(i>N)Q.pop_back();//找不到下一个点
}
}
}
return sum;
}
POJ1273
POJ3436
POJ2112
有流量上下界的网络最大流

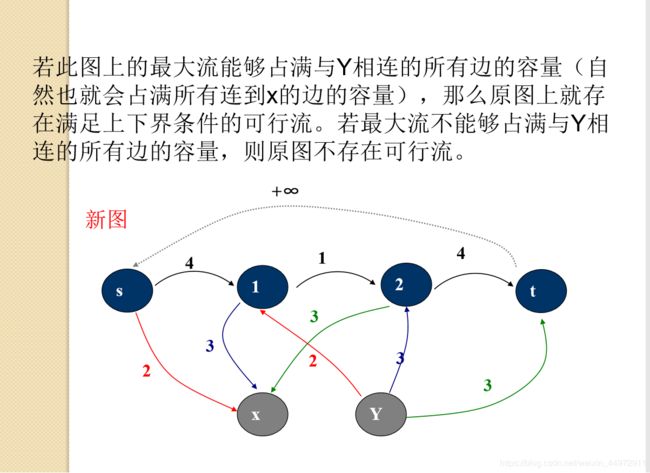
在新图中做一遍最大流,得到sum1。
然后去掉s->t ,t->s 的边。
去掉和x,y相连的边。
以s为源,t为汇再做一次最大流,得到sum2。
sum = sum1 + sum2
设新图为G2,两次最大流后的残余网络是G,流量下界为L
各边的流量为:G2[i][j]-G[i][j]+L[i][j]
POJ2396
15、博弈
HDU1847
POJ1067
Nim
有2个玩家;
n堆石头:t1,t1,t3…tn;
每次选择一堆,取走任意个石头
谁先取完谁获胜
1、若t1 ^ t2 ^ t3 ^ … ^ tn == 0 先手败
2、否则,先手胜。
POJ1704
SG函数
把原问题变成nim问题
int f[110];//限制取
int sg[10010];//sg函数数组
bool visit[10010];
void sg_do(int n,int k)
{
memset(sg,0,sizeof(sg));
for(int i=1;i<=n;i++)
{
memset(visit,0,sizeof(visit));
for(int j=1;j<=k;j++)
{
if(i-f[j]>=0&&j<=k)//对于每个 i 能到达的点
{
visit[sg[i-f[j]]]=true;
}
for(int j=0;j<=n;j++)//sg函数运算(找最小非负整数)
if(!visit[j])
{
sg[i]=j;
break;
}
}
}
}
HDU1536
HDU3980
POJ2425
16、欧几里得,中国剩余定理
int gcd(int a,int b)//最大公约数
{
if(b==0)return a;
else return gcd(b,a%b);
}
int lcm(int a,int b)//最小公倍数
{
return a/gcd(a,b)*b;
}
扩展欧几里得
//ax+by = gcd(a,b)
int ex_gcd(int a,int b,int &x,int &y)//求x,y
{
if(b==0)
{
x=1,y=0;
return a;
}
int d = ex_gcd(b,a%b,x,y);
int tap = x;
x = y;
y = temp - a/b*y;
return gcd;
}
a x + by = c ---------x0,y0 为一个解,则通解为:
x = x0 + b * t / gcd ------------------- t为任意整数
y = y0 - b * t / gcd
POJ2142
POJ2115
线性同余方程,中国剩余定理
x mod 3 = 2
x mod 5 = 4
x mod 7 = 6
前两项方程可以合并为一个新的方程,然后逐项向下合并。
合并时运用扩展欧几里得,还可以判断是否有解。
HDU1573
HihoCoder1303
HDU3430
17、其他数学定理
费马小定理
P是质数:
P不能整除a:a^(P-1) %P == 1
P能整除a:a^(P-1) %P == 0
欧拉定理
定义欧拉函数 φ(n) :求小于n的整数中与n互质的数的个数
φ(1) = 1
φ(n) = n - 1 (n为质数)
a,n 为正整数,若gcd(a,n)==1:
a^φ(n) %n == 1
指数爆炸的时候就要降幂
就是求
a^b mod c
可以转化为
a^( b mod phi(c ) +phi(c ) ) mod c
//欧拉函数
ll phi(ll n)
{
ll i,rea=n;
for(i=2;i*i<=n;i++)
{
if(n%i==0)
{
rea=rea-rea/i;
while(n%i==0)
n/=i;
}
}
if(n>1)
rea=rea-rea/n;
return rea;
}