乘积最大【题解】
代码已经摆在下面了。 【原题】请点击这里
下面简单说一下题目内容:
给定一个长为N(6<=N<=40)的数字字符串(其实用int数组也可以),往它们中间塞入K(1<=K<=6)个乘号,
使形成的算式结果(乘积)最大。
“区间DP与其余DP有别”
所以在理解与解题是不应该以其他的DP思路为基础(不然会很凌乱)。这是一道划分型区间DP。
首先要抓住DP的共性:
求出子问题最优解,使每个子问题包含其子问题中的最优解。区间DP同一问题(相比之下)包含更多的子问题最优解,
所以可以简单理解为:枚举“区间”,也就是说,线性动规每个点可能就只有2个左右的来源,而这一题的每个子问题的最优解要牵扯到多个来源。
下面开始美妙的分析:
(1)影响每一个状态的玩意儿有:当前长度i(或者说是位置),当前已使用的h个乘号(*);
(2)通过简单的思考:如果我们想求出:在前i个数中,用h个乘号的情况下的最大乘积(即一个子问题的最优解)。那么,我们就需要,把这其中所有
的组合方式的乘积记录一遍,再在它们中找到最优解(这叫“状态更新”),记为此状态(i,h)的最优解。
(3)综上,我们要做的事情顺序如下:枚举范围(i,h)——在当前范围中枚举所有解,找出的全部解中选出最优的(max/min)——记为当前状态最优解
【由于大范围依附于小范围,所以范围的枚举从小到大!】
现在,快睡着的朋友们,也许下面有幅图片会产生更好的理解效果。
首先我把关键代码摆出来:
#include
#include
#define go(i,a,b) for (i=a;i<=b;i++)
using namespace std;
int a[60],f[1000][1000],sum[60][60];
int main()
{
int n,k,i,j,h;
cin>>n>>k;go(i,1,n){scanf("%1d",&a[i]);sum[i][i]=a[i];}
go(i,1,n)go(j,i+1,n)sum[i][j]=sum[i][j-1]*10+a[j];
go(i,1,n)f[i][0]=sum[1][i];
go(h,1,k)go(i,h+1,n)go(j,h,i-1){f[i][h]=max(f[i][h],f[j][h-1]*sum[j+1][i]);}
cout< cin>>n>>k;go(i,1,n){scanf("%1d",&a[i]);sum[i][i]=a[i];}go(i,1,n)go(j,i+1,n)sum[i][j]=sum[i][j-1]*10+a[j];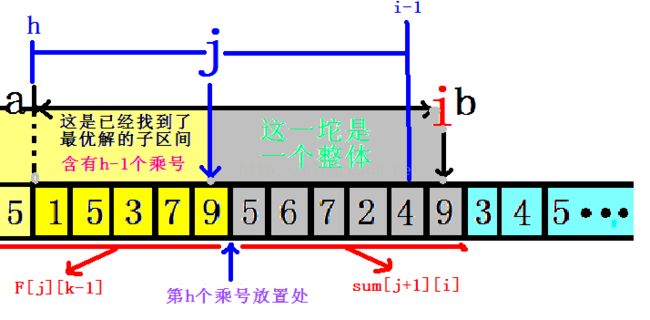
好,非常好,张姐!现在开始分析DP核心程序,看这里(建议认真看图):
go(h,1,k)go(i,h+1,n)go(j,h,i-1){f[i][h]=max(f[i][h],f[j][h-1]*sum[j+1][i]);
【注意:这道题读入的是K,现在的循环变量是h】。h表示当前你准备往一堆数中塞入第h个乘号(在这之前,已经有h-1个乘号被你塞到了这堆数中,但你要知道,这堆数不一定是你读入的整堆数,可以视作子问题一枚)。i表示什么?(你可以随时瞟一眼上面的图),在图中,我们发现,i的箭头走在最前面(a,b无实义),我们可以这样讲:h和i两个变量在这整堆数中划分出一个区域(枚举区间),然后变量j则在它俩之间运动(即图中a,b两点之间,不包括端点),那么j就将该区域划分成两部分,设这两部分为A(h~j),B(j+1~i)。我们令前一部分A区间已经完成了最优解的枚举,将第h个乘号放在j处(这里特指j所在数的尾巴上),再令B区间是一个整体(不含乘号)。因此,A区间是用其状态f[][]表示,B区间则是用sum[][]表示的。别忘了j是在h和i之间运动的,所以它每走一步,就可以产生新的A,B区间,并将这些不同的A,B区间组合进行比较,找出其中的最优解(也就是乘积最大的搭配方式)。当然,j是不能运动到h上,因为这样B区间就消失了!最后一点是:你要有足够的勇气与理解能力去相信,A区间里面已经存了它的最优解(因为循环是从小到大进行的)。
现在,就看DP方程了(
f[i][h]的含义:在前i个数中放入h个乘号,所得到的最大乘积
)
f[i][h]=max(f[i][h],f[j][h-1]*sum[j+1][i]
由于f[i][h]每次要与多个f[j][h-1]*sum[j+1][i]所以用max来不断更新“最优解”。其实,本质上就是枚举A,B两区间的最大值,然而A,B两区间的内容取决于当前i,j,h的值。
张姐需要再次重申的是f[i][h]的含义(看上面),所以:f[i][h]的最优值取决于在它的范围之内各个区间中只放h-1个乘号的状态中的最优解,即f[j][h-1]*sum[j+1][i]。
好,非常好。下面这幅图展示了一个状态的枚举过程:
最后,说明两个问题。
(一)为什么枚举的区间的左边界是h而不是1。因为在循环中,h代表当前的放置乘号的个数,所以第h个乘号必须放在第h个数的右侧。举个例子:比如现在该放第3个乘号了,那么这个乘号能够放在第1个数或是第2个数后面吗?我们注意到图中的淡黄色区域,那表示已经找到最优解的区间,那么里面就存了前两个乘号,再怎么说,我们也应该给他俩留两个位置吧,比如这样放:“2*7*6*17637361”,所以第3个乘号只能从第3个数开始放。
(二)还有一个预处理没讲。当h为1时,f[i][h]就成了f[i][0],这里面是没有值的,所以我们需要下面这句话:
go(i,1,n)f[i][0]=sum[1][i];
这道题的个人理解就是这样,如有纰漏,欢迎指出!
在此,推荐几道区间DP的典型例题:(第一个和本题是划分型DP,其余为归并型DP)
数字游戏 能量项链 石子归并【1】 石子归并【2】