C++信息学奥赛题目归类:2007-2018年初赛普及组问题求解
2007
题目一
(子集划分)将n个数(1,2,…,n)划分成r个子集。每个数都恰好属于一个子集,任何两个不同的子集没有共同的数,也没有空集。将不同划分方法的总数记为S(n,r)。例如,S(4,2)=7,这7种不同的划分方法依次为{(1),(234)},{(2),(134)},{(3),(124)},{(4),(123)},{(12),(34)},{(13),(24)},{(14),(23)}。当n=6,r=3时,S(6,3)=______________。 (提示:先固定一个数,对于其余的5个数考虑S(5,3)与S(5,2),再分这两种情况对原固定的数进行分析。)
求解思路: 将n个数划分成k个子集,表示成:S(n , k),其中n代表了数字的个数,k代表了子集的个数。
这个题的提示是让你按照递归调用的方式去思考的
所以S(n,k) = S(n-1,k-1) + k*S(n-1,k)
答案:90
题目二
(最短路线)某城市的街道是一个很规整的矩形网络(见下图),有7条南北向的纵街,5条东西向的横街。现要从西南角的A走到东北角的B,最短的走法共有多少种?

求解思路:可以发现从西南到东北角最短要走10条短线,而且其中必有4条为竖线,从10条短线中选出4条作为路线中的竖线,也就确定了整条线路,所以一共有C10,4=210种路线(从10条线中选出6条横线一样)
答案:210
2008
题目一
书架上有4本不同的书A、B、C、D。其中A和B是红皮的,C和D是黑皮的。把这4本书摆在书架上,满足所有黑皮的书都排在一起的摆法有_____种。满足 A必须比C靠左,所有红皮的书要摆放在一起,所有黑皮的书要摆放在一起,共有______种摆法。
求解思路:第一步:把2本黑色的书当成一个整体,和其他两本书全排列,就是P(3,3)=6;第二步:由于2本黑色的书是不同的书,所以这2本是可以交换位置的,再乘上一个2.
所以就是P(3,3)×2=12
由于“A必须在C左边”,而且同颜色的还要在一起,所以就只能是两个红色的在左边,两个黑色的在右边.
所以就是P(2,2)×P(2,2)=4
答案:12 4
题目二
有6个城市,任何两个城市之间都有一条道路连接,6个城市两两之间的距离如下表所示,则城市1到城市6的最短距离为_____________。

求解思路:城市顺序为1-2-5-6
答案:7
2009
题目一
小陈现有2个任务A,B要完成,每个任务分别有若干步骤如下:A=a1->a2->a3,B=b1->b2->b3->b4->b5。在任何时候,小陈只能专心做某个任务的一个步骤。但是如果愿意,他可以在做完手中任务的当前步骤后,切换至另一个任务,从上次此任务第一个未做的步骤继续。每个任务的步骤顺序不能打乱,例如……a2->b2->a3->b3……是合法的,而……a2->b3->a3->b2……是不合法的。小陈从B任务的b1步骤开始做,当恰做完某个任务的某个步骤后,就停工回家吃饭了。当他回来时,只记得自己已经完成了整个任务A,其他的都忘了。试计算小陈饭前已做的可能的任务步骤序列共有[ ]种。
现在要把这段程序分配到若干台(数量充足)用电缆连接的PC上做并行执行。每台PC执行其中的某几个语句,并可随时通过电缆与其他PC通讯,交换一些中间结果。假设每台PC每单位时间可以执行一个语句,且通讯花费的时间不计。则这段程序最快可以在[ ]单位时间内执行完毕。 注意:任意中间结果只有在某台PC上已经得到,才可以被其他PC引用。例如若语句4和6被分别分配到两台PC上执行,则因为语句6需要引用语句4的计算结果,语句6必须在语句4之后执行。 1——2——4——6——7 第一时间1,第二时间2和3,第三时间4和5,第四时间6,第五时间7。 LZW编码是一种自适应词典编码。在编码的过程中,开始时只有一部基础构造元素的编码词典,如果在编码的过程中遇到一个新的词条,则该词条及一个新的编码会被追加到词典中,并用于后继信息的编码。 举例说明,考虑一个待编码的信息串:“xyx yy yy xyx”。初始词典只有3个条目,第一个为x,编码为1;第二个为y,编码为2;第三个为空格,编码为3;于是串"xyx"的编码为1-2-1(其中-为编码分隔符),加上后面的一个空格就是1-2-1-3。但由于有了一个空格,我们就知道前面的"xyx"是一个单词,而由于该单词没有在词典中,我们就可以自适应的把这个词条添加到词典里,编码为4,然后按照新的词典对后继信息进行编码,以此类推。于是,最后得到编码:1-2-1-3-2-2-3-5-3-4。 现在已知初始词典的3个条目如上述,则信息串"yyxy xx yyxy xyx xx xyx"的编码是_________。 根据题目信息找出相应的规律,然后解码 队列快照是指在某一时刻队列中的元素组成的有序序列。例如,当元素1、2、3入队,元素1出队后,此刻的队列快照是"2 3"。当元素2、3也出队后,队列快照是"",即为空。现有3个正整数元素依次入队、出队。已知它们的和为8,则共有_________种可能的不同的队列快照(不同队列的相同快照只计一次)。例如,“5 1”、“4 2 2”、""都是可能的队列快照;而"7"不是可能的队列快照,因为剩下的2个正整数的和不可能是1。 所以全部加起来总共1 6 21 21=49个 每份考卷都有一个8位二进制序列号。当且仅当一个序列号含有偶数个1时,它才是有效的。例如,0000000、01010011都是有效的序列号,而11111110不是。那么,有效的序列号共有_____个。 定义字符串的基本操作为:删除一个字符、插入一个字符和将一个字符修改成另外一个字符这三种操作。将字符串A变成字符串B的最少操作步数,称为字符串A到字符串B的编辑距离。字符串“ABCDEFG”到字符串“BADECG”的编辑距离为_____。 如果平面上任取n个整点(横纵坐标都是整数),其中一定存在两个点,它们连线的中点也是整点,那么n至少是__________。 在NOI期间,主办单位为了欢迎来自各国的选手,举行了盛大的晚宴。在第十八桌,有5名大陆选手和5名港澳选手共同进膳。为了增进交流,他们决定相隔就坐,即每个大陆选手左右旁都是港澳选手,每个港澳选手左右旁都是大陆选手。那么,这一桌一共有_______种不同的就坐方案。 注:如果在两个方案中,每个选手左右相邻的选手相同,则视为同一种方案。 7 个同学围坐一圈,要选 2 个不相邻的作为代表,有_________种不同的选法。 某系统自称使用了一种防窃听的方式验证用户密码。密码是n 个数 s1, s2, ⋯ , sn,均为 0或 1。该系统每次随机生成 n 个数 a1, a2, ⋯ , an,均为 0或1,请用户回答 (s1a1 + s2a2 + ⋯+ snan) 除以 2 的余数。如果多次的回答总是正确,即认为掌握密码。该系统认为,即使问答的过程被泄露,也无助于破解密码——因为用户并没有直接发送密码。 把M个同样的球放到N个同样的袋子里,允许有的袋子空着不放,问共有多少种不同的放置方法?(用K表示)。 例如,M=7,N=3时,K=8;在这里认为和是同一种放置方法。 问:M=8,N=5时,K=___ 。 如图所示,图中每条边上的数字表示该边的长度,则从A到E的最短距离是__。 第二步:k=3 有四条路到F,用d3(C,E)、d3(C,F)、d3(D,F)、d3(D,E)来表示这四条路,3表示第三阶段。 重新排列 1234 使得每一个数字都不在原来的位置上,一共有__种排法。 一棵结点数为 2015 的二叉树最多有___个叶子结点。 从一个 4 \times 44×4 的棋盘(不可旋转)中选取不在同一行也不在同一列上的两个方格,共有_______种方法。 约定二叉树的根节点高度为 1。一棵结点数为 2016 的二叉树最少有()个叶子结点;一棵结点数为 2016 的二叉树最小的高度值是( )。 一个人站在坐标(0, 0)处,面朝 x 轴正方向。第一轮,他向前走 1 单位距离,然后右转;第二轮,他向前走 2 单位距离,然后右转;第三轮,他向前走 3 单位距离,然后右转……他一直这么走下去。请问第 2017 轮后,他的坐标是:( _________ , _________ )。(请在答题纸上用逗号隔开两空答案) 如下图所示,共有 13 个格子。对任何一个格子进行一次操作,会使得它自己以及与它上下左右相邻的格子中的数字改变(由 1 变 0,或由 0 变 1)。现在要使得所有的格子中的数字都变为 0,至少需要_________次操作。 第二次:第四排中间那个 第三次:最上面那个 甲乙丙丁四人在考虑周末要不要外出郊游。 已知①如果周末下雨,并且乙不去,则甲一定不去;②如果乙去,则丁一定去;③如果丙去,则丁一定不去;④如果丁不去,而且甲不去,则丙一定不去。 如果周末丙去了,则甲________,乙________,丁________,周末________。 因为丁没去,由②知:乙没去; 因为丁没去,丙去了,由④知:甲去了; 因为甲去了,乙没去,由①知:周末没下雨; 从 1 到 2018 这 2018 个数中,共有__________个包含数字 8 的数。求解思路:
先选出了b1———a1———a2———a3
然后依次把b2,b2和b3,b2和b3和b4,…向里面插。并且满足bi的位置要<=bj (i答案:70题目二
1. a=1;
2. b=a;
3. d=-a;
4. e=a+d;
5. c=2*d;
6. f=b+e-d;
7. g=a*f+c;
求解思路:
可以画出一个拓扑图
——3——
————5——答案:52010
题目一
求解思路:答案:2-2-1-2-3-1-1-3-4-3-1-2-1-3-5-3-6题目二
求解思路:
第一个是""
一位数一共有6个
然后两位数
1 1 到 1 6 共6个
2 1到 2 5 共5个
3 1到 3 4 共4个
4 1 到4 3共3个
5 1到 5 2 共2个
6 1到 6 1 共1个
总共1 。。 6=21个
最后三位数
1开头 116 125 134 143 152 161
2开头 215 224 233 242 251
同理可得 总共 6 5 。。 1=21
答案:492011
题目一
求解思路:
8个二进制各不干涉 且只有2中选择即0或1 满足题意的序列号即为有0个1的序号 2个1的序号 4个1的序号 6个1的序号 8个1的序号
1+28+70+28+1=128
序列号中有0个1的有1个 序列号中有2个1的有28个 4个1的有70个 6个1的有28个 8个1的有1个
答案:128题目二
求解思路:
就是把ABCDEFG变成BADECG的步骤需要几步
把A变成B,B变成A,C删除,F变成C答案:42012
题目一
求解思路:
先选出了b1———a1———a2———a3
然后依次把b2,b2和b3,b2和b3和b4,…向里面插。并且满足bi的位置要<=bj (i答案:5题目二
求解思路:
相当于1个圆,十个人。先随便找个座,让人去坐,有10个可能,然后顺时
针走,下一个座就有5种可能,再下一个就4个,再下一个还是4个,以此类推,
就是10 * 5 * 4 * 4 * 3 * 3 * 2 * 2 * 1 * 1。这其中有重复的,同一种坐法,可以绕着桌子走
一圈,就是上一个人坐到下一个人的位置,串一下,这样所有坐法就算重复了10次,
再除以10就行了。就是5 * 4 * 3 * 3 * 2 * 2 * 1 * 1.答案:28802013
题目一
求解思路:
任选其中一个的方案是7,另选4,乘法原理7*4=28,两两重复除2,得14;答案:14题目二
然而,事与愿违。例如,当n = 4 时,有人窃听了以下5 次问答:
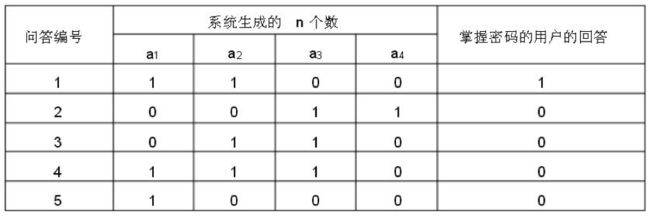
就破解出了密码s1 =___ ,s2 = ,s3 = ,s4 =___。
答案格式为:纯数字用,连接求解思路:
用5可以推出(s1 * 1 + 0 + 0 + 0)% 2 == 0,s1 * 1 == 0,s1 == 0;
把s1 == 0代入1可得(0 * 1+s2 * 1+0+0)% 2 == 1,s2 * 1 == 1,s2 == 1;
把s2 == 1代入3可得(0+1 * 1 + s3 * 1+0)% 2 == 0,s3 * 1 == 1,s3 == 1;
把s3 == 1代入2可得(0 + 0+1 * 1 + s4 * 1)% 2 == 0,s4 * 1 == 1,s4 == 1;答案:0,1,1,12014
题目一
求解思路:答案:18题目二
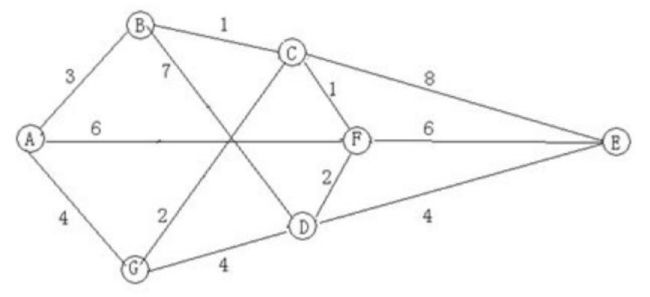
求解思路:
这个题目是动态规划的一个变型题目,从A到E划分为四个阶段,每个阶段都要决策,前一阶段的终点就是后一阶段的起点,对前一阶段的状态作出某种决策,产生后一阶段的状态。
2014NOIP普及组初赛 二、问题求解2.如图所示,图中每条边上的数字表示该边的长度,则……
我们可以用倒推的方法,求A到E的最短距离。用k来表示阶段。
第一步:k=4 有 d4(F,E)来表示F到E的距离,4表示第四阶段。
f4(F)=6
f3©=min{d3(C,E)、d3(C,F)}
=min{8,1+6}=7
f3(D)=min{d3(D,F)、d3(D,E)}
=min{2+6,4}=4
第三步:k=2 有
f2(B)=min{d2(B,C),d2(B,D)}
=min{1+7,7+4}=8
f2(G)=min{d2(G,C),d2(G,D)}
=min{2+7,4+4}=8
第四步:k=1有
f1(A)=min{d1(A,B),d1(A,G),d1(A,F)}
=min{3+8,4+8,6+6}=11
答案:11 。答案:112015
题目一
求解思路:
穷举:
2 1 4 3
2 4 1 3
2 3 4 1
3 1 4 2
3 4 1 2
3 4 2 1
4 1 2 3
4 3 1 2
4 3 2 1答案:9题目二
求解思路:
二叉树有一个性质,即叶子节点 = 度为2的节点数+1
所以二叉树叶子节点最多的时,即度为2的节点数也最多,这种情况出现完全二叉树树种, 2015个节点的完全二叉树。
2015 = 叶子节点N0 + 度为1的节点N1+ 度为2的节点N2
当N1 = 0时,N0 = 1008 ,最多有1008个。答案:10082016
题目一
求解思路:
任选一个,去掉同列同行4+4-1=7个,剩16-7=9个
16*9=144
考虑有类似 (a,b) (b,a) 重复的情况
144/2=72答案:72题目二
求解思路:答案:1,112017
题目一
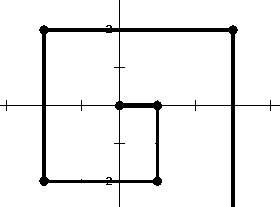
求解思路:
1: x+i
2: y-i
3: x-i
4: y+i
2017/4 == 504…1
x = (1-3+5-7) 重复504次 == -1008
y = (-2+4-6+8) 重复504次 == 1008
在进行1次循环到 (x+2017, y) -> (1009, 1008)答案:1009,1008题目二
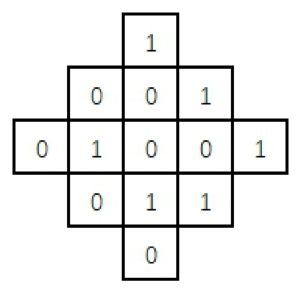
求解思路:
第一次:第三排右数第二个答案:32018
题目一
求解思路:
因为丙去了,由③知:丁没去;题目二
求解思路:
1-----99有19个数含8,
100----199有19个数含8,
…
800----899有100个数含8
…
1800-----1899有100个数含8,
2000-----2018有2个数含8
一共有:
(20-2)×19+2×100+2
=18×19+202
=342+202
=564个答案:564