堆 及 堆排序

堆

定义: 一种特别的树状数据结构.
一个堆满足的特性:

1. 给定堆中任意节点P和C，若P是C的母节点，那么P的值会小于等于（或大于等于）C的值”。若母节点的值恒小于等于子节点的值，此堆称为最小堆（min heap）
2. 若母节点的值恒大于等于子节点的值，此堆称为最大堆（max heap）

堆的实现

堆的实现通过构造二叉堆（binary heap），实为二叉树的一种

二叉树:是每个节点最多只有两个分支（即不存在分支度大于2的节点）的树结构.

而堆的实现是靠二叉树中的 完全二叉树实现的.

完全二叉树:对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树.

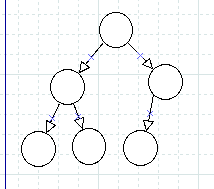
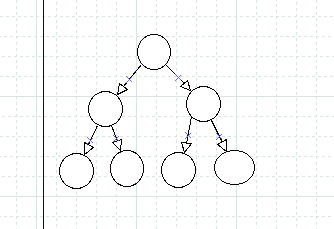
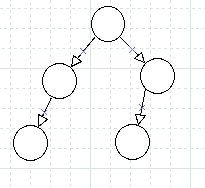
完全二叉树 如下图 都是完全二叉树:

                     

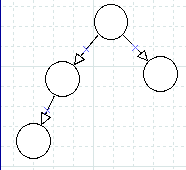
非完全二叉树

即:完全二叉树满足 每一层都是连续集中在左侧;

此处用数组 来存储完全二叉树.

根节点的下表为 1.
若有一个结点 i, (假设 i 结点有父节点且 有 左子树和右子树),则 其父节点的下标为 i/2,左子树 的 下标为 2*i右子树的下表为 i*2+1.

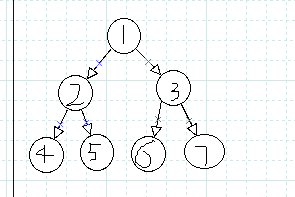
有两种 增加结点的方法.
1.从根结点( 1 )开始,然后 2, 3 . 每次增加一个结点后向上调整.
2. 先将总结点数的 一半 加在最底层(从左往右),然后 开始从倒数第二层开始,每次增加一个结点都向下调整.

以大根堆 为例:

这里就涉及二叉树的一些性质了.
如果 $i=1$,则结点 i 是二叉树的根,无双亲; 如果 i > 1,则其双亲为 $\lfloor i/2\rfloor$.
如果 $2\ast i>n$,则结点 i 无左孩子(结点 i 为叶子结点);否则其左孩子是结点 $2\ast i$
如果 $2\ast i+1>n$,则结点 i 无右孩子,否则其右孩子是结点 $2\ast i+1$

向上调整:

每次调整前先判断 这个结点是否为 根结点 即.

		if(i == 1)  return ;  // i 为 待调整的点

若不是根节点 则判断 该结点 与 该节点的父节点的大小,若 该结点大,则 该节点于父节点互换位置,继续向上 判断,直到 该节点 是父节点 或 该节点没有 父结点 大 时退出.

       while(i != 1)
        {
                if(h[i] < h[i/2])  swap(i,i/2);    
                else  break;
                
                i = i/2;
        }

向下调整:

假设 待插入的结点为 i.
每次 需要先判断 i结点是否存在 左子树,若存在 则进行判断,不存在则退出.

用 变量 temp 备份当前 最大 的结点.

先 判断 i 和 左儿子 的大小, 有temp 备份最大值.
判断 i 是否有 右儿子,若有 则用 temp 与 i 的 右儿子 比较,用 t 备份最大值.
若没有 右儿子则不用进行判断

然后 判断 i与 temp 是否相等. 若 (i == temp) 则代表 当前 i 是最小的 值,退出.
否则 交换 temp 与 i,继续进行判断

        while(i * 2 <= n)
        {       
                //判断和左儿子的关系 
                if(h[i] < h[i*2])  t = i*2;
                else temp = i;
                
                //如果有 右儿子,
                if(i*2+1 <= n)
                {       
                        if(h[temp] < h[i*2+1])    t = i*2+1;
                }
                
                if(temp != i)
                {       
                        swap(temp,i);
                        i = temp;  
                }
                else break;
        }

到此,已经 建立了一个满二叉树. 之后需要做的 每次将 根拿出来,然后将 二叉树的 最后一个结点 放到 根的 位置,然后让根 向下调整.

此处,将 根节点 拿出放到 数组的最后一个位置,待 排序后, 即为 从小向大 排序.

void heapsort()
{
        while(n > 1)
        {
                swap(1,n);
                n--;
                siftdown(1);
        }

        return ;

}

假设 堆 如下图所示:

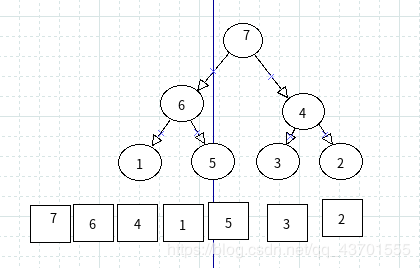
第一次 排序后 :

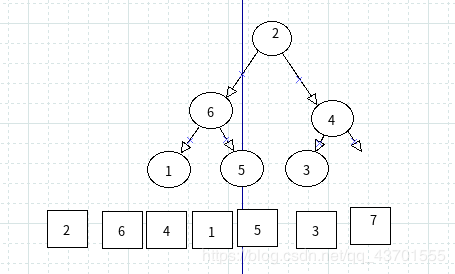
然后向下调整. 直到最后只剩下 根节点时结束.

#include

// 用数组 模拟二叉树
int h[101];   //用来存放堆的数组
int n;  //存储 堆 中的元素个数

void swap(int x,int y)
{
	int temp = h[x];
	h[x] = h[y];
	h[y] = temp;
	
	return ;
}

void siftdown(int i)   //向下调整
{
	int t;  //记录当前最大值
	int flag = 0;   //判断是否需要继续向下调整

	while(i * 2 <= n)
//	while(i * 2 <= n && flag == 0)
	{
		//判断和左儿子的关系
		if(h[i] < h[i*2])  t = i*2;
		else t = i;

		//如果有 右儿子,
		if(i*2+1 <= n)
		{
			if(h[t] < h[i*2+1])    t = i*2+1;
		}

		if(t != i)
		{
			swap(t,i);
			i = t;   //更新 i 为刚才与它交换的儿子结点的编号,便于向下调整
		}
		else break;
		/*else
		{
			flag = 1;  //否则 说明当前的父节点 已经比两个子节点都要大了,不需要继续进行调整
		}*/
	}

	return ;
}

/*void siftup(int i)  //向上调整
{
	int flag = 0;
	if(i == 1)  return ;   //已经是 根结点了
	while(i != 1 && flag == 0)
	{
		//判断是否比父节点 小
		if(h[i] < h[i/2])  swap(i,i/2);
		else  flag = 1;

		i = i/2;
	}
	return ;
}
*/

void heapsort()
{
	while(n > 1)
	{
		swap(1,n);
		n--;
		siftdown(1);
	}

	return ;

}

void creat()
{
	int i;
	for(i = n/2;i >= 1;i--)   siftdown(i);
	return ;
}

int main()
{
	int num,i;
	scanf("%d",&num);
	n = num;
	for(i = 1;i <= num;i++)   scanf( "%d",&h[i]);
	
	creat();  //建堆    大顶堆   
	
	//堆排序
//	heapsort();

	for(i = 1;i <= num;i++)  printf( "%d ",h[i]);
	

	return 0;
}