lecture9-提高模型泛化能力的方法

HInton第9课，这节课没有放论文进去。。。。。如有不对之处还望指正。话说hinton的课果然信息量够大。推荐认真看PRML《Pattern Recognition and Machine Learning》。

摘自PRML中22页。

正文：

一、提高泛化方法的概述

        在这部分中，将会介绍通过减少（当一个模型的数据表现能力大大的超过训练时提供的数据而产生的）过拟合来提高模型的泛化能力，将会介绍不同的方法去控制网络的数据表达能力，并介绍当我们使用这样一种方法的时候如何设置元参数，然后给出一个通过提早结束训练来控制网络能力（其实就是防止过拟合）的例子。

回顾前面的课程，过拟合的原因是因为和从输入映射到输出的映射中中有着真正规律性的信息一样，任何有限集合的训练数据同样包含采用误差。训练集中的偶然性的规律是因为搞好某些具体的训练样本被选中而已。

所以当我们拟合这个模型的时候，它不能说哪些规律性是真实的，并且当再次对训练集进行采样的时候还是存在的，而哪些规律性是由采样误差导致的。所以模型同时拟合了两种数据规律，如果模型太灵活了，它就会很好的对采样误差进行拟合，然后它的泛化能力就会很差。

所以我们需要方法来阻止过拟合，第一个方法也是目前最好的方法：就是简单的增加更多的数据，如果你能提供更多的数据，那么就不需要去提出更多花哨的方法了，数据永远有着防止过拟合的正确的特性，在假设你的电脑足够快的情况下，数据是越多越好的。

第二个方法就是试着对模型的能力进行约束，这样使得模型有足够的能力去拟合真实的规律性，但是却没有足够的能力去拟合由采样误差导致的虚假的规律性。当然这很难，随后会介绍各种方法去试图控制这个能力。

在下一课将会介绍关于许多不同模型的平均化，如果我们对有着不同形式的模型和犯着不同错误的模型进行均化，那么这个均化后的效果要好于单独的模型。可以通过在训练数据的不同子集上训练这些不同的模型。这种技术也叫做“bagging”。当然也有很多其他的方法去打乱数据使得模型都尽可能的不同。

第四种方法：也叫做贝叶斯方法，是通过使用一个单一的NN结构，但是却能找到许多不同的权重集合来很好的预测输出。然后再测试数据上，使用所有的这些不同的权重向量来均化这些预测的结果。

上图就是一些控制模型能力的方法。最显而易见的就是通过这个结构，通过限定隐藏层的数量和每层的单元的个数，这就控制了网络中连接的数量，也就是参数的个数。

第二个方法也是较为便利的方法就是以很小的权值开始，然后再快要过拟合的时候停止学习，也就是假设它已经找到了正确的规律，但是还没找到由特定的训练集所带来的错误的规律性，在本小结的最后会介绍这方面。

一个常见的方法去控制NN的能力就是通过给定隐藏层数或者每层的单元数量是从小到大，然后惩罚这些权重，通过使用惩罚项或者使用权值的平方值约束（就是L2范数）或者权重的绝对值（L 1范数）。

最后，可以通过对权重加上噪音的方法或者对激活值加上噪音的方法来控制模型的能力。

通常来说，我们使用这些不同的能力控制方法中的几种的组合方法。

对于大多数方法来说，有些元参数还是需要去设置的，就像隐藏单元的数量或者层数或者权值惩罚的尺寸（size，或者翻译成范围，规模）。一个显而易见的选择元参数方法就是在每个元参数中的每个参数都使用许多不同的值，例如：隐藏单元的数量，然后看当数量为多少的时候才是在测试集合上表现最好的时候。但是有时候这也是很错的方法，因为这就像说当你给出另一个测试集合的情况下这个方法的工作效果会有多好一样。所以在某个具体测试集上表现的最好的设置不可能说它也能够在一个来自同一个分布数据的新的测试集上工作很好，因为它们是在特定的测试集上调整好了的。也就是说给出一个模型可以在新的测试集上能有多好的效果一样的假象。

举个极端的例子：假设测试集合是完全随机的，就像很多的的金融数据一样，所以结果不是依赖于输入或者说不能从输入来预测输出，如果选择了一个在你自己的测试集合上最好结果的模型，那么它显然比在这个测试集上偶然结果要好，因为你选择的就是比偶然更好的结果，但是如果你在一个同样随机的新的数据上，那么就不可能期望它会比偶然性更好的结果，所以通过选择一个模型，那么就得到了一个假象：一个模型可以在新数据上工作的多好。那么问题就是有解决方法吗？

所以上图就是一个比选择元参数更好的方法。将数据分成三部分：训练，交叉验证和测试集合。验证集合不是用来训练的，而是用来决定如何选择元参数的。换句话说，就是看这个模型在验证集合上有多好的效果，然后再去决定一个大致的隐藏单元数量或者一个权重惩罚的尺寸。但是一旦你这么做了，那么就在验证集合上找出最好的参数集合，然后再第三个测试集合上进行测试，而且测试集合只能用一次，这会给出一个这个网络工作有多好的无偏估计，通常来说这这个估计会比验证集合差那么一点。

在近来的比赛中，组织比赛的人们都学会了先不动真正的测试数据，然后让人们发送预测结果这样他们就知道是否他们真的可以在真正的测试数据上很好的预测，或者他们是在验证数据上通过在具体的验证数据上选择的元参数而导致过拟合了，从而没法再新的测试集合上很好的泛化（也就是在举办比赛的时候，不会把真正的测试数据放出来，只放训练数据和验证数据，通过结果来发现你的结果是真的泛化还是过拟合什么的）。

一个可以得到更好的有关权值惩罚或者隐藏单元数量或者其他试图拟合验证数据的评估的方法是循环这个验证集合。所以先不动为了最后的无偏估计的真正的测试集合，通过将其他的数据划分成N个相等尺寸的子数据集，然后再其中的（N-1）个数据集上训练，然后将没有训练的那个作为验证集合（也就是切分成N等分，然后随机组合排列），所以就能够得到许多不同的权值惩罚的最好的估计，和单元数量的最好的数量。这也被称之为“N-fold cross-validation”,N

折交叉验证。要记得，这N个不同的估计之间不是相互独立的。例如，如果我们很不幸的，所有属于同一个类别的样本都落在了一个子集上，那么泛化能力就是相当差了，所以不论是这个子集在验证集合还是训练集合中，泛化能力都是很差的（这里的意思就是不要产生特定的同类别扎堆现象，最好都能很好的均匀随机分布）。

上图就是一个比较简单的防止过拟合的方法。，当在一个小的计算机上训练一个大模型的时候而且也没那么多时间去使用不同的隐藏单元数量或者不同的权值惩罚尺寸来训练多次的时候是很好的。你所要做的就是以小权值开始，然后随着模型的训练，不断的增大，然后盯着验证集合上的效果，一旦结果开始变差，那么就可以停止训练了。如果使用的是错误率而不是平方误差或者其他什么误差，那么在集合上的效果折线图也许会特别的波动。所以很难看出它什么时候该停止，所以通常要做的就是看着，然后确定事情真的变坏了，那么就退回到之前最好的那个点上。

这个方法的原理就是当以很小的权值开始的模型通常来说不会有多大的能力，而且这个权值也没有时间变大。有趣的是为什么小权值有着更低的能力。

考虑一个有着许多输入、许多隐藏单元和许多输出单元的模型，当权值很小的时候，如果隐藏单元是逻辑单元，那么他们总的输入将会接近于0，而且它们差不多会在线性范围的中间，也就是说它们的行为很像线性单元，意思就是当权值很小，整个网络和一个将输入直接映射到输出的线性网络是一样的。所以如果将权值矩阵W1乘以W2，那么就得到了一个用来连接输入和输出的权重矩阵，假设权值很小，那么一层逻辑隐藏单元的网络的行为就很像是线性网络了。同样假设我们将线性网络中的权重划分成四份，考虑这么一个事实：当对于隐藏单元来说，在线性区域中，他们是有着四分之一的斜面，所以它们的能力不比线性网络强多少。所以在这里显示的网络中，是3x6和6x2的权重，它的能力不比一个3x2的网络强多少。

按照这种方法增长，开始先使用序列的非线性区域，然后使用所有的这些参数，所以如果这个网络在开始的时候有6个权重，并以30个权重（3x6+6x2）结束.那么就可以认为这个网络的能力是平滑的随着权重变得更大的从6个参数过渡到30个参数（这里看来size应该翻译成规模的意思）。在早期停止所发生的就是在验证数据上有着尽可能正确数量的参数，也就是在拟合正确的规律性和具体选择的训练样本导致的错误的规律性之间的优化。

二、约束权重的大小（对比前面的尺寸，范围，规模的意思）

这部分将会介绍通过限制权重的大小来控制模型的能力，标准的方法就是通过引入一个惩罚项来防止权重变得太大，这里是包含一个隐藏的假设：有着很小权值的网络比有着大权值的网络更简单。有好几个不同的惩罚项可以使用，同样也可以限定权值来使得输入到每个隐藏单元的权重向量不允许比某个具体的长度要长（个人：这里是使用的欧式距离的长度，其实就是自身的平方再开根）。

标准的限制权重的大小的方法就是使用一个L2权重惩罚，也就是惩罚权重的平方值，在NN文献中有时候也叫做权重衰减，因为这个惩罚项的导数扮演着将权重强制推向0的行为。这个权重惩罚可以使得权值保持很小，除非它们有很大的误差导数来抵消掉，所以如果观察这个惩罚项像什么，就如上图中的矩形区域，权重如果远离0的话，那么就得到一个抛物线似的代价损失（cost）。；如果观察上图中的式子部分，所需要优化的损失（cost）就是试图减小的正常的误差，加上一个有着一个lambda前置系数的权重平方的和的项（C =E+。。那个式子），而且系数除以2，是为了求导的时候可以刚好抵消掉。在和项之前的系数有时候也叫做权重代价（weight cost），是用来决定这个惩罚的程度的。如果进行求导。可以发现cost的导数就是误差的导数加上某个具体的权重大小乘以lambda。当权重的大小是-（1/lambda）乘以误差关于权重大小的导数的时候，损失的导数是为0的。所以唯一使得权重变大的时候就是当损失函数达到最小值的时候，而且同时还拥有大误差导数的时候。这使得权重更容易被解释。所以你就不会有着整个权重集合中很多权重很大但是却没法做任何事的情况。

在权重上的L2惩罚的影响是为了防止网络使用不需要的权重。这也通常可以提高泛化能力，因为它能够阻止那些不需要的权重去拟合采样误差。同样的它还能使得模型更平滑，使得当输入改变的时候输出的改变会更缓慢。

所以如果网络有两个非常相似的输入，那么使用一个L2权重惩罚后，它更愿意使得在这两个相似的输入上权重减半，而不是所有的权重都是1.。上图右边部分：如果两个输入都是相似的，那么两个网络会输出相似的输出值，但是下面这个网络会当输入改变的时候输出有着更少的极端变化（就是变化比较缓慢，而上面那个一个为1 一个为0的，变化较为极端。）

上图是另一种权重惩罚方法。L1惩罚，这里损失函数是一个 “V”字形。所以这里我们所要作的就是惩罚权重的绝对值。这个方法的一个妙处在于可以使得许多的权重更接近于0，这有助于解释（很像权重稀疏化）。如果只有一点非0的权重留下，那么就更容易懂得网络会发生什么。

同样我们可以使用比L1还极端的权重惩罚（没说是什么惩罚，但是照推测，一个平方，一个绝对值，那么一个应该是开根号什么的吧），这里损失函数的梯度实际上随着权重变得更大的时候是会更小的（上图中红线在绿线之下）。这使得网络可以在没有将权值推向0的时候保持权重很大的情况。所以我们甚至更喜欢有着一些很大权重的情况出现。

这里的方法不同于在权重上放上惩罚，而是使用权重约束。意思是不采用惩罚每个权重的平方值，而是在每个隐藏单元或者输出单元的输入权重中的最大平方长度（欧式距离法则，向量长度的概念）上加上一个约束。当我们更新权重的时候，如果这个输入权重向量比约束的还长，那么就简单的对这个向量进行缩放直到长度匹配允许的长度（缩放的方法：通过对所有的权重除以相同的数量值来进行缩放，也就是整体缩放）。

像这样进行使用权重约束，比权重惩罚的一个好处在于：比选择使用权重惩罚额来说，更容易的对输入权重因子的平方长度设置合理的值，这是因为逻辑单元天生可以进行缩放所以我们就知道1的权重意味着什么。使用权重约束同样可以阻止当所有的权重都超小而且也做不了什么有用的事的时候隐藏单元被陷入接近于0的状况，因为当所有的权重都超小的时候，权重上也就没什么约束了，所以也没有东西可以阻止它们增长；权重约束同样可以阻止权重爆炸的情况。

权重约束中一个不易察觉的事情是当一个单元命中他的约束的时候，在所有的权重上的有效的惩罚是由大梯度决定的，所以如果某些输入权重有着大梯度，它们会试图将输入权重的长度因子往上推（值变大），这会将其他的权重往下推（值变小）。所以实际上，如果认为它像一个惩罚，这个惩罚会缩放他自己使得能够对大权重来说是合适的，而且能够压缩小的权重。这比一个固定惩罚去对不相关的权重往0的方向上推更有效，这些也就是la Grange 乘法，其中的惩罚就是La Grange 乘法需要能够满足约束。

三、使用噪音作为正则化

在这部分中，会介绍另一个约束NN网络能力的方法。可以通过不论是在权重还是在激活值上增加噪音。开始的部分会介绍，如果在一个简单的线性网络的输入部分增加噪音，然后试图对平凡误差进行最小化，也就是等于在网络的权重上使用L2惩罚。然后介绍在更复杂的网络中有关噪音权重的用处，最后介绍一个近来的发现：在激活值上极端的噪音同样可以作为一个很好的正则化器。

首先先介绍当在一个简单的NN的输入部分添加高斯噪音会发生什么事情。噪音的方差可以通过通过与下一层隐藏层中的连接的平方权重来进行放大。如果我们有个很简单的网络，只有一个线性输出单元去直接与输入相连，那么这个放大的噪音就会加到输出上。如上图右边部分，首先是一个输入Xi和额外的采样自0均值和方差sigma的平方的高斯的高斯噪音，这个额外的噪音是通过平方权重与其相乘的。然后输出到神经元 j 上，所以神经元 j 的输出前的部分（就是经过激活函数前的部分，这里不确定是前还是后，个人倾向于前）就是 yj + 有着0均值和wi平方乘以sigma i 平方的高斯噪音。额外的方差使得对平方误差来说有额外的贡献，可以认为这像pythagoras 理论，也就是平方误差是由yj和额外的噪音导致的平方误差的和，因为这个噪音与yj之间是独立的。如果它是个噪音-free系统，那么当我们最小化总的平方误差的时候，就能出现平方误差的最小化值。另外，我们还会对第二项进行最小化，也就是会最小化第二项的期望平方值，而这个期望平方值就是Wi2乘以sigma i2（就是上图中输出单元部分的高斯方差），所以这也相对应于一个在wi上和sigma i2上的L2惩罚。

上图就是数学上的解释，输出为y^noisy，假设当我们在所有的输入上加了噪音后，那么有着噪音-free系统的输出会变得怎样？在wixi上的输入的所有的和加上wi乘以epilision_i（也就是对每个输入增加的噪音）的所有的和，这些噪音都采样自一个0均值和方差为sigma_i的高斯分布。（第二行）所以如果我们计算这个期望平方误差（带有噪音的输出y^noisy和目标值 t 之间的误差），也就是上图中第二行的式子的左边部分。这里会使用一个E后面跟着平方括号来表示一个期望，这里不是表示误差，而是表示一个期望。计算这个期望的部分就是在这个平方括号中的部分，所以这里是计算从带有噪音的系统中得到的平方误差的期望（上图第二行应该看得懂，就不翻译了）。（第三行）当完成了这个平方后，首先得到的就是（y-t）^2，而这不再期望括号中是因为它不涉及到噪音；第二项是两项的交叉乘积，第三项就是最后一项的平方。现在这个式子简单多了。（第四行）事实上，如图中的解释，两者是独立的，所以它可以简化到正常的平方误差加上第四行的第二项，能够这么简化的原因是因为epsilion_i与epsilion_j是相互独立的，所以如果观察最后一项（第三行第三项），当在那个平方上相乘，所有的交叉乘积都得到一个期望值为0，因为是将两个有着0均值的独立项相乘的。如果观察中间的部分（第三行第二项），同样也有着期望为0的值，因为每个epsilion_i是与误差相独立的。所以我们可以重写第四行的式子为第五行。所以发现我们之前的期望平方误差只是一个噪音free系统中的平方误差加上一个额外的项。则看上去就像是在Wi上的一个L2惩罚项，并且有个惩罚项的强度系数sigma_i^2罢了。

在更复杂的网络中，我们可以通过在权重上增加高斯噪音的方式来约束模型的能力，这不完全等于一个L2惩罚，但是这看上去有更好的效果，特别是在递归网络中。所以AlexGrave近来在他的识别手写数字的递归网络的权重上增加噪音，实验表明效果更好了。

我们可以同样的在激活值上使用噪音作为一个正则化器，所以假设我们使用BP去训练一个有着逻辑隐藏单元的多层网络。如果我们在前馈中使单元是二值化和随机的，但是在后向传播上就像使用正常的确定性直传中使用实值那么会发生什么事情。所以我们是将逻辑单元在前馈中当成随机二值神经元，也就是我们计算逻辑P的输出，然后将P视为输出 1 的概率。在前馈中，使用的是概率随机来决策是否输出是1还是0。但是在后向路径中，使用p的实值作为后向传播的导数来通过这些隐藏单元。这不是很准确，但是它很接近一个为了随机系统所做的正确的事情，如果所有的单元都对上层的每个单元都有很小的贡献。

这么做的话，在训练集上的效果会更差，而且训练相对来说更慢了，而且是几倍的慢。但是在测试集上它很明显的会更好。这也是当前一个没公开发表的结果。

四、贝叶斯方法的介绍（这部分不推荐看，直接跳过，就是简单的贝叶斯规则，hinton老人家说的比较罗嗦，可以直接拿本统计书看看就得了）

这部分将会介绍贝叶斯的方法去拟合模型，通过使用一个简单的抛硬币的例子来讲解。贝叶斯的原理是不使用模型的参数最可能的设置，而是考虑所有可能的参数设置然后试着对每个可能的设置找出在给定数据下它的概率。

贝叶斯机制假设我们对于每件事总会有个先验分布，也就是说对于任何你所关心的事件来说，必须有关于这些事件会发生的先验概率。

先验也许是很模糊的；我们的数据会给我们一个似然项，我们可以通过我们的先验与它结合然后得到一个后验。这里的似然项是为了我们的参数的设置能够让数据更具可能性。它有可能会与先验冲突，但是在约束条件下，如果我们有足够的数据，那么不论先验多么的不可能，数据总是能够战胜它的，然后在最后（也就是预测的部分，即后验概率）有着足够的数据下，真实结果就会显现。也就是说即使你的先验是错的，但是却能得到正确的假设结果；但是如果你确信你的结果是不符合先验的，那么这也需要相当多的数据才能搞定的。

那么就讲解一个抛硬币的例子吧。假设完全不知道任何有关硬币的事情，除了它们可以被抛起和当抛完之后就可以得到任意一面，并假设每次事件之间都是相互独立的。所以我们的硬币模型就是只有一个参数P，这个参数P决定着这个硬币的关于结果是头朝上的概率。

假设抛了100次，得到53次头朝上的结果，那么这个参数P的值该是多少。当然一看，会说结果是0.53，但是有证据吗？最通常的答案就是，也被称之为最大似然，是为了选择一个使得观察结果最可能的参数值，而这个值就是0.53。可惜的是，这不正确。

所以一个包含53个头朝上和47个头朝下的序列的概率可以被写成每次抛的头朝上的结果p和头朝下的结果（1-p）的乘积，如上图第一行所示。如果现在问，在依赖p的情况下观察的数据的概率是多少，我们就可以对关于p进行求导，然后得到了上图中的结果，如果将这个导数设置成0，我们就发现这个当这个数据的概率最大化（看成一个函数，然后求导观察导数走势，在0的地方肯定是最大或者最小值）的时候，就是将p设置成0.53的时候，这也就是最大似然。

但是在使用最大似然去决定一个模型的参数也会遇到很多问题。假设那个例子，我们只抛一次，就得到一个头朝上，这不代表我们认为硬币的概率为1，这也就是说如果概率为1，那么在无限次的抛结果中都得不到头朝下的事件，这摆明不可能。直观的认为概率应该为0.5，但是如何来证明它。

更重要的是，我们可以合理的得到一个简单的答案吗。我们不知道，我们对数据知之甚少，所以也没法确定p的值是多少，所以我们真正该做的就是拒绝使用一个简单的答案，而是在所有的可能的答案上得到整个的概率分布，那么这样0.5看上去就相当可信了。所以结果为1的情况假设我们有一些先验置信而且在抛硬币抛到一半的时候也是那么不可能的（这句话意思就是值为1 不可能）。

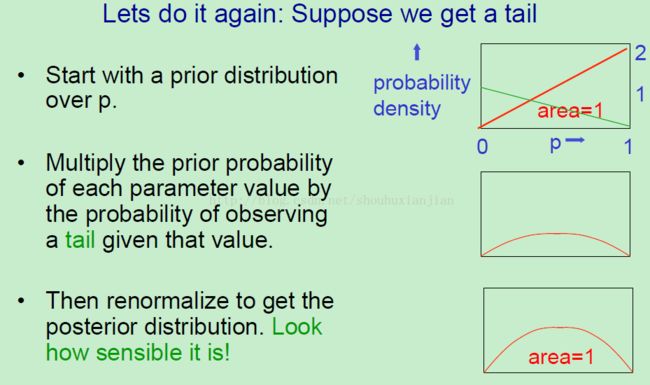
上图就是个例子，从使用基于参数值的许多先验分布来开始，然后得到一个很容易处理的后验分布，这里的结果不是我们通常认为的合理解释。（在随后会展示如果使用自适应贝叶斯方法的话，先验分布是怎么被数据自己所修改的。）所以这里先以基于所有的不同的p值的先验概率都相同的情况（第一个图）开始。我们认为硬币是存在不同程度上的偏移的（即硬币不是那么理想的均匀的）。而任何偏移上的数量都是相等的，即对于一些在半数时间上头朝上的硬币，与其他全部时间头朝上的硬币是一样的（即，就是得到的硬币之间我们认为都是一样的）。

我们现在观察一个头朝上的硬币的事件。也就是现在所要作的就是，对于p的每个可能的值，我们考虑它的先验概率，然后将观察到的头朝上的概率与其相乘，基于此的话，即正确的p的值就是1 了。所以，如果我们把p赋值为1，也就是说每次投掷的话头朝上的概率都是1了。如果p赋值为0，那么就刚好相反了。现在看上图右边的部分（第二幅图），红线就是我们的先验概率了，按照假设将所观察到的头朝上的概率乘以它，现在就得到了一个类似坡的，这是一个未标准化的后验概率，未标准化是因为红线下面的区域面积不是1，当然对于一个概率分布来说，所有的概率值加起来一定是等于1的。

所以最后我们所要做的就是进行再次的标准化，对每个值进行缩放，使得总和为1。现在如果以统一关于 p 的先验分布开始，然后以p的三角后验分布结束。

那么再来一次（上图第一个图），这次假设尾朝上在，所以这里的先验分布就是在观察一个头朝上的事件后得到的一个后连续分布，这里的绿线是按照关于p的值的每个假设的情况下得到一个尾朝上的概率。所以如果p等于1，那么观察到的概率就是0。所以我们需要将我们的先验与我们的似然项相乘。

那么就得到了一个曲线如上图第二个图。

然后进行再次标准化得到上图第三个图，这就是观察到一个头朝上和一个尾朝上后得到的一个后验分布了。注意到这是一个相当明智的分布。在观察到每个事件之后，就注意到p 不可能为0或者为1，它看上去最可能的应该是中间。

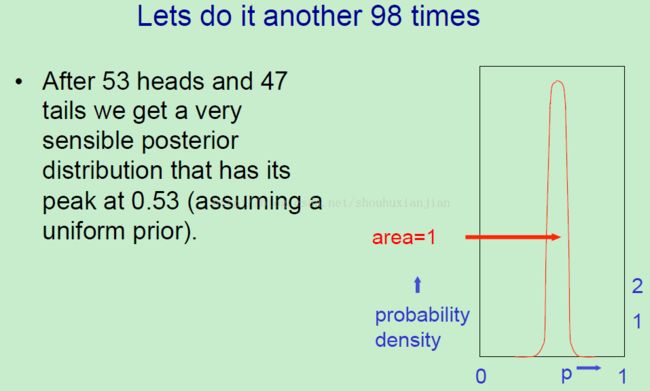
如果我们这么再次抛掷98次的话，同时使用同样的策略：在基于不同的p的值的情况下，将最后一次任务的后验概率乘以这次事件的观察的似然。并假设有53次头朝上和47次尾朝上。那么就得到上图右边那个图的形状，它的均值为53，是因为首先是以统一的先验开始的，然后在0.53的时候达到峰值。不过这也说明其他的值是49，这也是基于此曲线图下一个完美的合理的值。

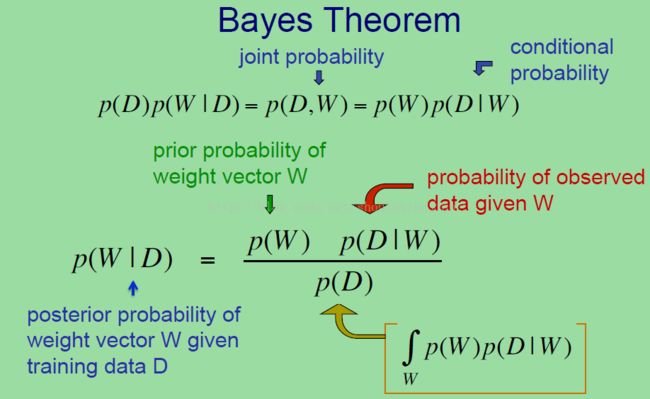
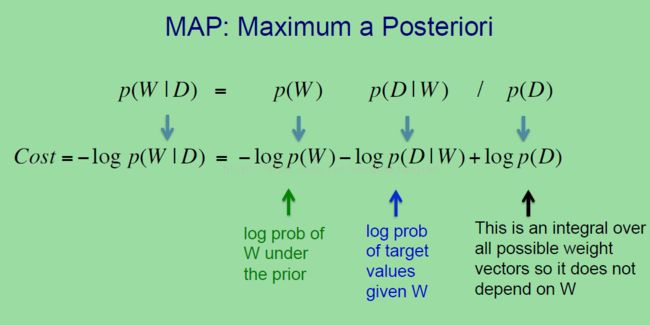
所以我们可以进行如下的总结：为了得到上图第一个公式中的中间那个关于参数W集合 和数据D的联合分布。对于监督学习来说，这个数据是由目标值（标签）组成的，所以我们假设在给定输入和由目标值组成的数据的情况下，这就是我们所观察到的。这个联合分布可以重写成一个独立概率乘以一个条件概率，所以上图第一个公式的第三部分，可以看出它与最左边的部分相等。

那么就得到了上图第二个公式，也就是通常的形式，也就是后验概率等于。。。。（这个就是我们概率书的第一课部分了。）因为上面式子的分母无关于求后验概率 W，所以其实它的存在与否也没关系。

五、权重衰减的贝叶斯解释

这部分将会介绍权重衰减的贝叶斯解释。在全贝叶斯方法中，我们试图计算模型中每个可能的参数集合下的后验概率，但是那是一个贝叶斯方法的相当简约的形式。简单的说去寻找一个单一参数集合，能够在先验概率和数据的之间最好的比较下的值，也被称为最大后验学习（MAP）。这也可以用来解释当使用权重衰减去控制模型能力的时候到底发生了什么。

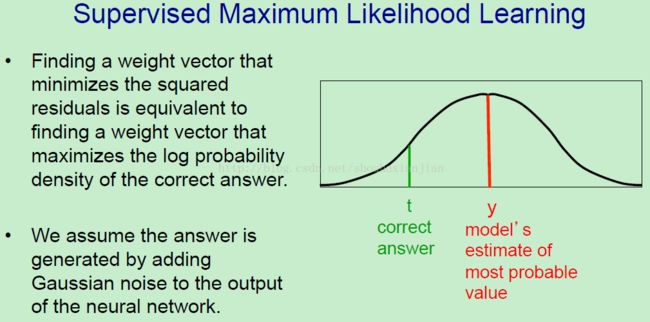
这里会介绍当在有监督最大似然学习的过程中最小化平方误差的时候会发生什么。即找到一个权重向量去最小化平方残差（就是目标值和网络的预测值之间的差异）等于找到一个权重向量去最大化有关正确解的log似然密度。为了找到这样的等式，我们需要假设这个正确值是由网络的输出加上高斯噪音形成的。所以原理就是：我们首先在基于输入的情况下运行一次这个网络得到一个预测值，然后加上高斯噪音，然后我们就会问了，这样做的正确的答案的概率是什么？

所以模型的输出就是高斯的中间（上图右边的图），我们所关心的就是希望在基于高斯的情况下目标值的概率最高，因为这个概率会生成 t ，这样的情况下网络会给出一个输出，即 y 是当高斯的中心在y 的时候 t 的 概率密度。

所以数学上看上去是这样的：假设基于训练样本c的网络的输出为yc，这个输出是由作用在输入c上的权值W一起生成的。那么基于输出值的情况下的目标值的概率就是在输出yc上加上由高斯中心在yc上的高斯噪音（上图第二个式子）。所以我们对基于高斯中心位于网络的输出的情况下目标值的概率密度很感兴趣。在上图第二个式子的右边部分，就是有着均值为yc的高斯分布，并也假设一些方差，在随后介绍。如果我们现在使用log函数，然后使用负号，那么就得到上图第三个式子，一个在给定网络输出yc的情况下目标值tc的概率 负log函数，是一个来自于对高斯的标准化的常数项加上指数的log项（上图第三个式子的右边部分）。即如果我们的损失韩式是关于正确解的负log分布，也就转换成最小化一个平方距离（上面第三个式子右边的tc-yc），这有助于了解当在使一个平方误差最小的时候，可以找到一个概率的解释，在这个概率解释中，就可以在基于高斯的情况下最大化log概率。

所以合适的贝叶斯方法就是找到基于所有可能的权重向量的情况下的全后验分布。如果有很多权重，那么当有个非线性网络的时候，这就变得即没希望而且很困难。贝叶斯有许多方法来逼近这个分布，比如Monte Carlo 方法，但是这次，我们试图让事情变得更简单一些。。

让我们找到这个最可能的权重向量，所以这个单一权重设置就是在知道先验知识的时候和数据的时候，找最可能的值。所以我们要做的就是找到W的最优值，通过使用随机权重向量初始化，然后将权重进行调整使得能够提升在给定数据的时候权重的概率；它有可能是个局部最优值。

现在在log领域工作会比概率更容易，所以如果我们想要最小化一个损失，那么就是用负的log函数。

这只是关于为什么我们最大化log概率的和或者最小化负的log概率的一方面。我们实际想要做的就是最大化数据的概率，也就是最大化基于不同训练样本下生成所有目标值的概率的积（就是本科上课的统计书上的最大似然）。如果我们假设这个输出错误是基于不同样本上互相独立的，我们就能可以写成上图中第一个式子那样。

log函数是单调的，所以在最大值的地方导数方向不会改变，所以不使用哪种最大化概率积的方法，而是最大化log每个概率的和的方法，这样更容易在计算机上运行，而且更稳定。所以就是上图第二个式子。

在最大后验学习中，我们试图找到权重的集合，它可以最优化基于拟合先验和拟合数据之间的权衡。上图就是基本原理。如果我们考虑负log去作为一个损失，那么就得到上图第二个式子，即左右都用上log。上图第二个式子中最后一个加的项就是基于所有可能的权重向量的积分，而且它不影响W，所以可以当最优化W的时候被忽略掉。式子右边第二项是在给定W的时候关于数据D的负log概率，这就是我们的通常的错误项（个人：这项其实也就是在考虑一个网络的情况下基于权重而生成的数据也就是输出部分，所以这也就是错误的来源的地方）。而右边的第一项只依赖于W是基于先验的情况下W的负log概率（这里的先验也就是对应于W的随机初始化）。

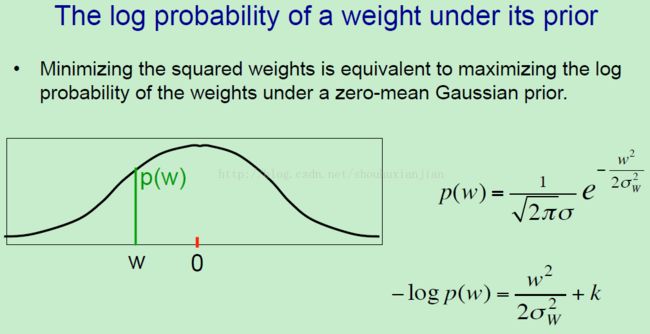
最大化一个权重的log概率也就是最小化一个平方距离，同样的道理，最大化生成正确目标值的log概率就是等同于最小化平方距离。所以最小化平方权重就等于最大化基于一个0均值的高斯先验的权重的log概率。所以这里是一个高斯（上图中的图），是一个均值为0，我们希望最大化这个权重的概率或者权重的log概率。也就是我们希望w能够尽可能的接近均值0。关于高斯的等式是如上图右边的式子，为0均值，所以我们不需要将它考虑进去。然后关于w的log概率就是平方权重被缩小2倍乘以方差，加上一个来自标准化高斯项的常量项，这个常数项当我们改变W的时候是不会被影响的。。

所以最后可以得到关于权重衰减或者权重惩罚的基本的解释。我们试图最小化在给定数据的时候权重的负log概率，这涉及到最小化依赖权重转变的一项，即我们如何转移目标并且确定这只依赖于权重。从给定权重的输出的log概率中推出，如果我们假设高斯噪音被加在网络的输出上，然后log概率是基于被缩小2倍乘以高斯噪音方差网络的的输出值和目标值之间的平方距离。相似的，如果我们假设一个权重的高斯先验，这个基于先验的权重log概率就是被缩小2倍乘以这个高斯先验方差的权重的平方值。所以现在将上图中第二个式子进行化简，得到第三个式子，将两边乘以2×数据方差的平方，我们就得到了一个新的损失函数，第一项就是当我们乘的过程中得到的简单的所有训练样本得到的预测值与目标值差异平方的和，这就是我们通常说的平方误差。这里的第二项现在变成了两个方差的比率乘以权重平方的和，所以你所看到的就是这两个方差的比率就是权重惩罚，所以我们最初的权重惩罚的想法就是一个试图让网络效果更好的数值，这里你需要通过使用验证集合来拟合权重惩罚的值，但是现在所见的就是如果我们使用这个高斯的解释，即高斯先验，那么对于这种关于网络输出与目标值关联的高斯模型，权重惩罚是由这些高斯方差决定的，而这只是这些高斯的比率罢了，这不是基于所有这些框架的一个随机值。

六、MacKay的固定权重损失的快速和脏（这个是字面意思）方法

这部分，介绍一个由David Mackay在1990年提出的方法，为了决定在一个没有使用验证集的NN中的权重惩罚。这是基于我们可以将权重惩罚解释成映射估计使得权重惩罚的大小与基于权重的先验分布的tightness（不知道怎么翻译合适）有关的。Mackay的方法说明我们可以经验性的拟合权重惩罚和假设在NN的输出中的噪音两个项去。为了得到不需要验证集和而且拟合权重的方法，这样就能允许我们可以在不同的子集上拥有不同的权重惩罚去作为NN中的连接，这些链接在验证集合上的代价很大。mackay 在使用这种方法赢得了比赛。

这里介绍一个由David Mackay提出的简单的，实用的方法，即我们可以将权重惩罚解释成两个方差的比率。在我们学到一个模型去最小化平方误差的时候，我们就能找到关于输出方差的最好的值，这个最好的值是通过简单的残差误差的方差来找到的。

我们同样可以子权重的高斯先验中估计这个方差，我们需要猜测这些方差应该是什么值来作为开始，然后做一些学习，然后使用一个非常脏的技巧，被称之为“经验性贝叶斯”。我们将我们的先验的方差设置成学到的模型的权重的方差，因为这个方差可以让这些权重最相似。这真的违反了许多贝叶斯方法的前提。我们使用数据去决定我们的先验置信该是什么。所以一旦我们学到了权重，我们使用一个0均值的高斯去拟合学到的权重的一维分布。然后我们考虑这个高斯的方差，然后将它作为我们的先验。现在一个美妙的事情就是，不同的权重子集。就像在不同的层中一样，例如，我们可以从不同的层中学习不同的方差。我们不需要验证集和，所以我们可以使用所有非测试数据去训练这个模型，因为我们不需要验证集和去决定不同层中的惩罚项，所以我们实际上可以有许多不同的权重惩罚。而这是很难用验证集和来得到的。

所以这就是Mackay的方法，以猜测噪音方差的值和权重先验方差的值作为起始。实际上，所有你所需要做的就是猜测这个比率。然后做一些梯度下降学习去改善这些权重。然后从新设置这些噪音方差成为残差误差的方差，并从新设置权重的先验方差成为实际学到的权重的分布的方差。

然后回到这个循环的开始部分再来一遍。所以这在实际中是很实用的。Mackay用这种方法赢得了一些比赛。

这节课就是说的如何以贝叶斯的观点来看待NN，然后使用一些看起来莫名其妙的方法来训练，不过那么问题就来了，为什么这个1990年发明的方法现在没人用了，是不符合正统数学观点，还是它的作用的确有限？？？