深入学习区块链的隐私保护(二)一大波盲签名算法
盲签名是由David Chaum提出的一种特殊签名方式,盲签名允许消息拥有者先将消息盲化后,把盲化后的消息发送给签名者进行签名,最后消息的拥有者对签名进行去盲因子处理,得到原消息的签名。盲签名就是接收者在不让签名者获取所签署消息具体内容的情况下所采取的一种特殊的数字签名技术,盲签名需要满足如下两个特殊性质:
- 签名者不知道所签署消息的具体内容
- 当签名消息被公布后,签名者无法知道这是他哪次签署的
根据不同的公钥密码体制构造依赖于不同密码假设下的盲签名方案,通常使用的有基于RSA的盲签名算法、基于Elgamal的盲签名算法、基于ECC的盲签名算法以及最近很火的基于格的盲签名。下面依次介绍(除了基于格的盲签名,格真是太难了)。
1 基于RSA的盲签名
消息m的拥有者选取一个随机数r,使得![]() ,N为RSA中的模数,即选择一个与N互素的数,对消息m的盲化,计算如下:(其中
,N为RSA中的模数,即选择一个与N互素的数,对消息m的盲化,计算如下:(其中![]() 为盲因子,e为签名者的公钥。)
为盲因子,e为签名者的公钥。)
![]()
消息的拥有者发送![]() 给签名者,签名者的私钥为d,公钥为e,签名者进行如下计算:
给签名者,签名者的私钥为d,公钥为e,签名者进行如下计算:
![]()
签名者将s'发送给拥有者,拥有者进行去盲因子处理,进行如下计算:
![]()
由于RSA中公私钥对的性质,使得![]() ,因此,消息m的签名是s,正确性如下:
,因此,消息m的签名是s,正确性如下:
![]()
2 基于Elgamal的盲签名
首先介绍下Elgamal的签名算法,其中p为一个大素数,g为![]() 中的一个生成元,若私钥为
中的一个生成元,若私钥为![]() ,对应的公钥为
,对应的公钥为![]() ,过程如下:
,过程如下:
- 签名过程:Bob对消息m进行签名,私钥为sk,公钥为pk。Bob随机选取
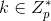 ,并计算
,并计算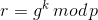 ,和
,和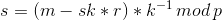 ,将签名信息
,将签名信息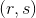 以及消息m发送给Alice。
以及消息m发送给Alice。 - 验签过程:Alice检验等式
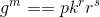 是否成立,若成立则签名确实由Bob生成。
是否成立,若成立则签名确实由Bob生成。
下面我们来介绍基于Elgamal的盲签,假设Alice和Bob的公私钥对分别为![]() 、
、![]() ,Alice需要Bob为消息m进行盲签名。过程如下:
,Alice需要Bob为消息m进行盲签名。过程如下:
- Alice盲化消息m: 随机选取盲因子
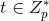 ,需满足
,需满足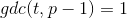 ,然后计算盲化后的消息
,然后计算盲化后的消息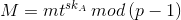 。
。 - Bob签名盲化后的消息:首先,随机选取
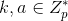 ,计算
,计算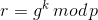 ,
,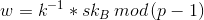 。然后计算
。然后计算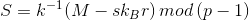 ,最后将
,最后将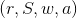 作为签名发送给Alice。
作为签名发送给Alice。 - Alice去盲化:去盲化后消息m的签名为
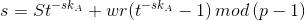 ,判断恢复出的签名是否正确,
,判断恢复出的签名是否正确,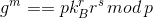 。此时消息m的签名信息为
。此时消息m的签名信息为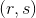 。
。
Remarks:公式的正确性推导,手算一下就行了,即(r,s)是否为正确的签名结构。
3 基于ECC的盲签名
椭圆曲线算法可以看作是定义在特殊集合下数的运算,满足一定的规则。椭圆曲线在如下两个域中定义:
![]() 域,素数域,p为大素数;
域,素数域,p为大素数;
![]() 域,特征为2的有限域,称之为二元域 或者二进制扩展域。在该域中,元素个数为
域,特征为2的有限域,称之为二元域 或者二进制扩展域。在该域中,元素个数为![]() 个。
个。
我们只介绍素数域。一些术语说明如下:
- 椭圆曲线的阶:椭圆曲线所有点的个数,包含无穷远点;
- 椭圆曲线上点的阶:若P为椭圆曲线上的点,nP=无穷远点,n取最小整数,即n为P的阶。
- 基点:椭圆曲线参数之一,用G表示,是椭圆曲线上的一点;
- 余因子:椭圆曲线的余因子,用h表示,为椭圆曲线点的个数/基点的阶。
- 椭圆曲线参数:素数域:
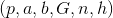 ,其中p为素数,确定
,其中p为素数,确定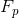 ,a和b确定椭圆曲线的方程,G为基点,n为G的阶,h为余因子。
,a和b确定椭圆曲线的方程,G为基点,n为G的阶,h为余因子。
首先介绍下ECDSA,假设签名者的公私钥对为![]() ,其中
,其中![]() ,
,![]() ,G为基点,为消息m进行签名。
,G为基点,为消息m进行签名。
签名过程如下:
- 随机选取一个整数
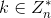 ;
; - 并计算
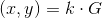 ,
,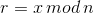 ,如果r=0,则返回1重新选择;
,如果r=0,则返回1重新选择; - 计算
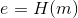 ;
; - 计算
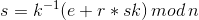 ,如果s=0,则返回1重新选择。
,如果s=0,则返回1重新选择。
签名者将签名![]() 和消息m发送给验证者,验证者进行验签,验签过程如下:
和消息m发送给验证者,验证者进行验签,验签过程如下:
- 验证r,s属于[1,n-1]中的整数;
- 计算
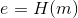 ;
; - 计算
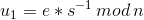 ,
,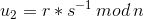 ;
; - 计算
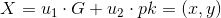 ,如果X=(0,0)则拒绝,否则计算
,如果X=(0,0)则拒绝,否则计算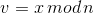 ,当且仅当v=r时,验证通过。
,当且仅当v=r时,验证通过。
Remarks:算法正确性的判断,计算生成(x,y)的是否是kG即可。
基于ECC的盲签名有很多方案,我们介绍最为经典的一个方案,Schnnor盲签名。椭圆曲线的参数如上,签名者Bob的公私钥对为![]() ,其中
,其中![]() ,并且Bob每次盲签名都会新生产一对临时签名公私钥对。用户Alice想让签名者对消息m进行盲签名,流程如下:
,并且Bob每次盲签名都会新生产一对临时签名公私钥对。用户Alice想让签名者对消息m进行盲签名,流程如下:
- Bob生成临时签名公私钥: 随机选取
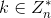 ,计算
,计算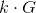 ,并将
,并将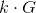 发送给Alice;
发送给Alice; - Alice对消息进行盲化:随机选取
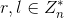 ,计算
,计算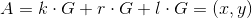 。令
。令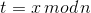 ,计算
,计算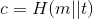 ,将
,将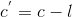 发送给Bob;
发送给Bob; - Bob签名盲化后的消息:计算
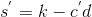 ,并发送给Alice;
,并发送给Alice; - Alice去盲化:计算
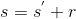 ,
,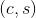 即为消息m的签名信息。
即为消息m的签名信息。
PS:肯定有小伙伴对Schnnor盲签名的结果有所疑惑,签名结果与ECDSA的签名信息不一致,这是因为Schnnor盲签名的结果对应于Schnnor签名,Schnnor签名与ECDSA是两种不同的基于ECC的签名方案,欲知后事,请听下回详细分解。