最近在做PAT时发现图论的一些题目需要对多条最短路径进行筛选,一个直接的解决办法是在发现最短路径的时候就进行判断,选出是否更换路径;另一个通用的方法是先把所有的最短路径记录下来,然后逐个判断。前者具有一定的难度并且不好排查BUG,因此我设计了一种基于Dijkstra的记录所有最短路的简捷算法,用于解决此类题目。
我们知道,Dijkstra是解决单源最短路问题的,并且最基本的算法仅能求出最短路的长度,而不能输出路径,本文基于Dinjkstra进行改进,使之能记录源点到任意点的所有最短路径。
使用vector
约定:结点编号为0到N-1,源点为0,到每个点的最短距离存储在数组minD[N]中。
在Dijkstra算法初始化时,找出所有源点的邻接点w并且把相应的最短距离minD[w]更新,同时初始化这些点w的第一条最短路径0->w(实现方法为分别push_back 0和w)。接下来将会找到一个到源点最短的点v,并且把v并入集合,对v的所有未访问的邻接点,如果到达w的路径(0->...->w)在包含v之后(0->...->v->w)变短,则删除w之前所有的最短路径,并且更新为到v的所有最短路径加上w点(注意对每个到v的最短路径都要这样处理);如果到达w的路径在包含v之后长度不变,说明发现了一条新的最短路径,在w原来最短路径容器的基础上再压入一个新的最短路径,这条路径为所有到v的最短路径加上w点。
经过这样的运算,就可以得到所有结点的所有最短路径了,下面以一个实例对算法进行测试,并且附上源代码。
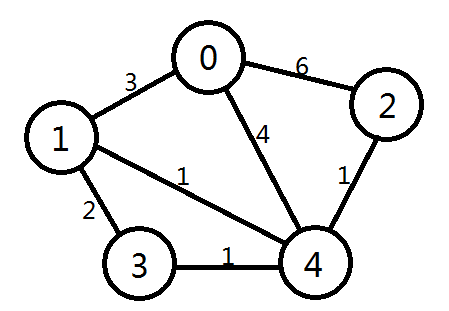
题目:求下图的源点0到所有结点的最短路径。
输入:
5 8
2 4 1
0 1 3
0 2 6
1 3 2
1 4 1
3 4 1
3 2 1
0 4 4
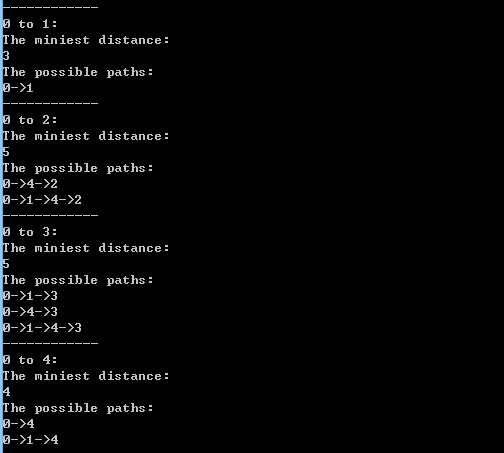
输出:
源码为:
#include
#include
#include
using namespace std;
#define MAX 1001
#define INF 99999999
int G[MAX][MAX];
int minD[MAX];
int minDist;
int finalSet[MAX];
int main()
{
int N,M;
int v1,v2;
int len;
cin >> N >> M;
for(int i = 0; i < N; i++){
finalSet[i] = 0;
minD[i] = INF;
for(int j = 0; j < N; j++)
G[i][j] = INF;
}
for(int i = 0; i < M; i++){
scanf("%d%d%d",&v1,&v2,&len);
G[v1][v2] = G[v2][v1] = len;
}
vector > > nodes(N);
// 设0为源点,计算从0到所有点的所有最短路径
finalSet[0] = 1;
minD[0] = 0;
// 首先把所有源点邻接点的最短距离初始化为源点到这些点的距离
for(int i = 1; i < N; i++){
if(G[0][i] != INF) {
minD[i] = G[0][i];
vector > minPaths;
minPaths.clear();
vector pathList;
pathList.clear();
pathList.push_back(0);
pathList.push_back(i);
minPaths.push_back(pathList);
nodes[i] = minPaths;
}
}
// 从所有minD中找出最小的,并入集合S,重复N-1次(源点已经加入集合)
for(int i = 1; i < N; i++){
minDist = INF;
int v = -1; // 记录到源点记录最小的结点
for(int w = 1; w < N; w++){
if(!finalSet[w] && minDist > minD[w]){
minDist = minD[w];
v = w;
}
}
if(v == -1) break; // v = -1说明找不到点了,当图不连通时才会出现这种情况
// 已经找到了到源点最近的点v,将其并入集合,并且考虑原来的最短距离0->...->W在加入了v之后有没有可能变短
// 如果变短了,就更新为0->...>v->W
finalSet[v] = 1;
for(int w = 1; w < N; w++){
if(!finalSet[w]){
int newD = minDist + G[v][w];
if(newD < minD[w]){
minD[w] = newD;
vector > minPathsV = nodes[v];
vector pathList;
nodes[w].clear();
for(int index = 0; index < minPathsV.size(); index++){
pathList = minPathsV[index];
pathList.push_back(w);
nodes[w].push_back(pathList);
}
}else if(newD == minD[w]){
vector > minPathsV = nodes[v];
vector pathList;
for(int index = 0; index < minPathsV.size(); index++){
pathList = minPathsV[index];
pathList.push_back(w);
nodes[w].push_back(pathList);
}
}
}
}
}
for(int i = 1; i < N; i++){
cout << "------------" << endl;
cout << "0 to "<< i << ":" << endl;
cout << "The miniest distance:" << endl << minD[i] << endl;
cout << "The possible paths:" << endl;
vector >minPaths = nodes[i];
int size = minPaths.size();
vector pathList;
for(int j = 0; j < size; j++){
pathList = minPaths[j];
int pathSize = pathList.size();
for(int k = 0; k < pathSize - 1; k++){
cout << pathList[k] << "->";
}
cout << pathList[pathSize - 1] << endl;
}
}
return 0;
}