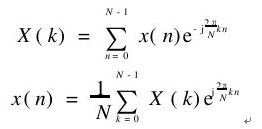FFT对信噪比的增益计算

1. 傅里叶变换也就这四种情况,那么从这四种情况中我们可以概括出他们的规律,即:

    非周期<--->连续

          周期<--->离散

    这个规律对于时域和频域上的信号是对称的。例如，如果时域上是非周期的,则频域上的信号肯定是连续的；如果时域上的信号时周期的,则频域上的信号肯定是离散的。反之亦然.

     2.  数字信号处理其实主要就是处理最后一种形式,即在时域和频域上都是离散的周期信号的傅里叶变换。DFT定义：

                    【1】

 

    模拟信号经过采样之后形成了一串数,在计算机中就使用数组来存储,也就是上面公式中的x(n),n就是n个采样点。那么经过转换后,X(k)则是用来存储不同频率点上的幅值。k相当于频域上的采样次数。 

  频率点k可以从0开始一直取下去,但每个频率点的间隔即频率的分辨率Ferr则是由采样率SRate和时域上所取的采样点数N来决定的,即有下列的关系:

    Ferr=SRate/N

    举例来讲,如果采样率是44KHZ,即1秒钟采样了44K个采样点,在实际应用中,假如我们只取了其中的连续的22K个采样点进行分析,那么这时N==22000,那么X(k)存储的分别是的频率为0HZ,2HZ,4HZ,8HZ.....点上的幅值,也就是说,这是X(k)的频率的分辨率为44KHZ/22K=2HZ。

 

3.  怎样更感性理解DFT呢？相量即是其中的一种方法。

   什么是相量？相量法？

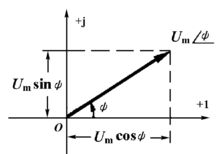
   析正弦稳态的有效方法是相量法，相量法的基础是用一个称为相量的向量或复数来表示正弦电压和电流。相量由正弦电压的振幅Um和初相ψ构成，复数的模表示电压的振幅，其幅角表示电压的初相。

   

相量是电子工程学中用以表示正弦量大小和相位的矢量。当频率一定时，相量唯一的表征了正弦量。将同频率的正弦量相量画在同一个复平面中（极坐标系统），称为相量图。从相量图中可以方便的看出各个正弦量的大小及它们之间的相位关系。

 从上面DFT的数学表达式【1】可以看出，X(k)可以看做是N个相量相加的结果。就相量相加而言，在什么情况下其值最大呢？显然是各个相量具有相同相位的情况下。因此，若x(n)与exp(-j*2*pi/N*k*n)共轭对称时，X(k)必将有一个峰值；如果不共轭对称，而是随着x(n)*exp(-j*2*pi/N*k*n)这个相量相角的增大，X(k)对应的值将相应减小；当x(0)*exp(-j*2*pi/N*k*0)与x(N-1)*exp(-j*2*pi/N*k*(N-1))的相位相差2*pi时，X(k)为0。

 在实际应用中，经常要估计DFT之后的信噪比，也即是说估计DFT的增益。利用相量的观点，也很容易得到结果。比如，一个单频信号，已经被噪声污染，如果进行1024点的DFT，信号的信噪比能增加多少dB?答案是约为30dB。因为信号是同相叠加，其幅度增加N倍；噪声是非同相叠加，其幅度增加N的开根号倍。因此DFT增益为

             20*Log10 [N/(N)0.5]=10* Log101024=30dB

 

实际上，在信号处理中，最重要的基础之一是要求系统的线性性。而在线性性的要求中，重要的一条就是叠加性。因此，对信号的线性处理，如DFT、滤波等，都可以从相量叠加这个角度去理解。在工程实践中，这种理解非常直观，往往会有意想不到的收获。

 

4.   频率分辨率   （解析度也叫分辨率）

     频率分辨率可以理解为在使用DFT时，在频率轴上的所能得到的最小频率间隔：

 f0=fs/N=1/NTs=1/T                                                       【2】

  其中N为采样点数，fs为采样频率，Ts为采样间隔。

 NTs就是采样前模拟信号的时间长度T，所以信号长度越长，频率分辨率越好。

是不是采样点数越多，频率分辨力提高了呢？其实不是的，因为一段数据拿来就确定了时间T，注意：f0=1/T，而T=NTs，增加N必然减小Ts ，因此，增加N时f0是不变的。只有增加点数的同时导致增加了数据长度T才能使分辨率越好。

还有容易搞混的一点，我们在做DFT时，常常在有效数据后面补零达到对频谱做某种改善的目的，我们常常认为这是增加了N（采样点数），从而使频率分辨率变好了，其实不是这样的，补零并没有增加有效数据的长度，仍然为T。但是补零其实有其他好处：

一：使数据N为2的整次幂，便于使用FFT。

二：补零后，其实是对DFT结果做了插值，克服“栅栏”效应，使谱外观平滑化；我把“栅栏”效应形象理解为，就像站在栅栏旁边透过栅栏看外面风景，肯定有被栅栏挡住比较多风景，此时就可能漏掉较大频域分量，但是补零以后，相当于你站远了，改变了栅栏密度，风景就看的越来越清楚了。

三：由于对时域数据的截短必然造成频谱泄露，因此在频谱中可能出现难以辨认的谱峰，补零在一定程度上能消除这种现象。

那么选择DFT时N参数要注意：1.由采样定理：fs>=2fh，2.频率分辨率：f0=fs/N，所以一般情况给定了fh和f0时也就限制了N。

 

5：百度百科中关于【频率分辨率】的定义

定义

频率分辨率是指将两个相邻谱峰分开的能力。在实际应用中是指分辨两个不同频率信号的最小间隔。研究数字频谱最有效方法通常是离散傅里叶变换。

频率分辨率=采样频率/DFT点数

频率分辨率：对模拟信号频谱的采样间隔

提高频率分辨率的方法：频谱细化

 

  理解：从5中可以看出，4中对频率分辨率的理解是错误的，fuck！怪不得看不懂，原来是错误的啊！只要采样频率不变，时域上采样点的个数多寡也不应该跟频率分辨率扯上关系啊！