3-基本数据结构
基本数据结构
- 3.基本数据结构
- 3.1 目标
- 前置基础 : ==数据, 数据元素, 数据项 和 数据对象==
- 3.2 什么是线性数据结构
- 3.3 什么是栈
- 3.4 栈的抽象数据类型
- 3.5 python实现栈
- 3.6 简单括号匹配
- 3.7 符号匹配
- 3.8 十进制转换成二进制
- 3.9 中缀前缀和后缀表达式
- 3.10 什么是队列
- 3.11 队列抽象数据类型
- 3.12 Python实现队列
- 3.13 模拟:烫手山芋
- 3.14 模拟:打印机
- 3.15 什么是Deque
- 3.16 Deque抽象数据类型
- 3.17 Python实现Deque
- 3.18 回文检查
- 3.19 列表
- 3.20 无序列表抽象数据类型
- 3.21 实现无序列表:链表
- 节点Node类:
- 无序列表类:
- 3.22 有序列表抽象数据结构
- 3.23 实现有序列表
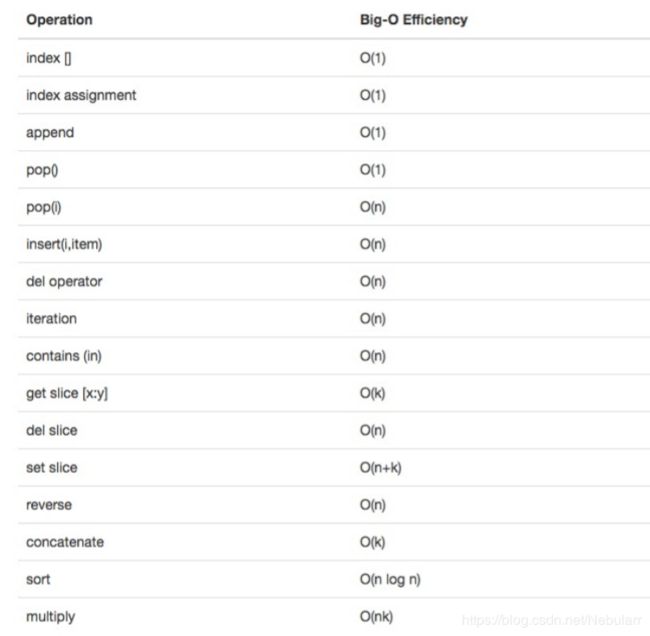
- 列表的时间复杂度
- 3.24 总结
3.基本数据结构
3.1 目标
- 理解抽象数据类型的 栈,队列,deque 和列表。
- 能够使用 Python 列表实现 ADT 堆栈,队列和 deque。
- 了解基本线性数据结构实现的性能。 了解前缀,中缀和后缀表达式格式。
- 使用栈来实现后缀表达式。
- 使用栈将表达式从中缀转换为后缀。
- 使用队列进行基本时序仿真。
- 能够识别问题中栈,队列和 deques 数据结构的适当使用。
- 能够使用节点和引用将抽象数据类型列表实现为链表。
- 能够比较我们的链表实现与 Python 的列表实现的性能。
前置基础 : 数据, 数据元素, 数据项 和 数据对象
数据:生活中充满了各种数据,其实数据不光是我们常见的文本字符,也可以是图像,声音,视频等等.
数据元素:是组成数据的、有一定意义的基本单位,在计算机中通 常作为整体处理。也被称为记录。
比如,在人类中,什么是数据元素呀?当然是人了。
畜类呢?哈,牛、马、羊、鸡、猪、狗等动物当然就是禽类的数据 元素。
数据项:一个数据元素可以由若干个数据项组成。数据项是数据不可分割的最小单位.
比如人这样的数据元素,可以有眼、耳、鼻、嘴、手、脚这些数据 项,也可以有姓名、年龄、性别、出生地址、联系电话等数据项, 具体有哪些数据项,要视你做的系统来决定。
数据对象:数据对象:是性质相同的数据元素的集合,是数据的子集。
什么叫性质相同呢,是指数据元素具有相同数量和类型的数据项, 比如,还是刚才的例子,人都有姓名、生日、性别等相同的数据 项。
既然数据对象是数据的子集,在实际应用中,处理的数据元素通常 具有相同性质,在不产生混淆的情况下,我们都将数据对象简称为 数据。
| 数据 | ||
|---|---|---|
| 数据对象 | ||
| 数据元素 | 数据元素 | 数据元素 |
| 数据项 | 数据项 | 数据项 |
3.2 什么是线性数据结构
我们从四个简单但重要的概念开始研究数据结构。
栈,队列,deques, 列表 是一类数据的容 器,它们数据项之间的顺序由添加或删除的顺序决定。
一旦一个 数据项 被添加,它相对于前 后元素一直保持该位置不变。诸如此类的数据结构被称为线性数据结构。
线性数据结构有两端,有时被称为左右,某些情况被称为前后。你也可以称为顶部和底部, 名字都不重要。
将两个线性数据结构区分开的方法是添加和移除项的方式,特别是添加和移 除项的位置。例如一些结构允许从一端添加项,另一些允许从另一端移除项。
(排队,一个拉一个,有限长的队伍.插队和离队的方式不一样.有的从尾插尾离,有的尾插头离)
3.3 什么是栈
栈(有时称为“后进先出(LIFO)栈): 是一个项的有序集合,其中添加移除新项总发生在同一端。这一 端通常称为“顶部”。与顶部对应的端称为“底部”。
生活中的一摞图书,盘子等都可以看作栈.
想想这种反转的属性,你可以想到使用计算机的时候所碰到的例子。
例如,每个 web 浏览器 都有一个返回按钮。当你浏览网页时,这些网页被放置在一个栈中(实际是网页的网址)。 你现在查看的网页在顶部,你第一个查看的网页在底部。如果按‘返回’按钮,将按相反的顺序 浏览刚才的页面。
3.4 栈的抽象数据类型
栈的抽象数据类型由以下结构和操作定义。如上所述,栈被构造为项的有序集合,其中项被 添加和从末端移除的位置称为“顶部”。栈是有序的 LIFO 。栈操作如下:
Stack()创建一个空的新栈。 它不需要参数,并返回一个空栈。push(item)将一个新项添加到栈的顶部。它需要 item 做参数并不返回任何内容。pop()从栈中删除顶部项。它不需要参数并返回 item 。栈被修改。peek()从栈返回顶部项,但不会删除它。不需要参数。 不修改栈。isEmpty()测试栈是否为空。不需要参数,并返回布尔值。size()返回栈中的 item 数量。不需要参数,并返回一个整数。
例如,s 是已经创建的空栈,Table1 展示了栈操作序列的结果。栈中,顶部项列在最右边。
| 栈操作 | 栈内容 | 返回值 |
|---|---|---|
| s.isEmpty | [ ] | True |
| s.push(4) | [4] | |
| s.push(‘dog’) | [4,“dog”] | |
| s.peek() | [4,“dog”] | ‘dog’ |
| s.push(True) | [4,“dog”,True] | |
| s.size() | [4,“dog”,True] | 3 |
| s.isEmpty | [4,“dog”,True] | False |
| s.push(8,.4) | [4,“dog”,True,8.4] | |
| s.pop() | [4,“dog”,True] | 8.4 |
| s.pop() | [4,“dog”] | True |
| s.size() | [4,“dog”] | 2 |
3.5 python实现栈
我们通过创建新类的方式实现一个新的数据结构:栈(Stack),并利用Python内置的列表类型来实现.
class Stack(object):
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[-1]
def size(self):
return len(self.items)
s = Stack()
print(s.isEmpty())
s.push(4)
s.push('dog')
print(s.peek())
s.push(True)
print(s.size())
print(s.isEmpty())
s.push(8.4)
print(s.pop())
print(s.pop())
print(s.size())
Note pythonds 模块包含本书中讨论的所有数据结构的实现。它根据以下部分构造:基本数据类型,树和图。
该模块可以从 : https://pypi.org/project/pythonds3/ 下载。
3.6 简单括号匹配
括号必须以匹配的方式出现。括号匹配意味着每个开始符号具有相应的结 束符号,并且括号能被正确嵌套。考虑下面正确匹配的括号字符串:
( ( )( )( )( ) )
( ( ( ( ) ) ) )
( ( ) ( ( ( ) ) ( ) ) )
对比那些不匹配的括号:
( ( ( ( ( ( ( ) )
( ) ) )
( ( )( ) ( ( )
思路:
----利用栈来实现,首先对整个括号字符串进行遍历,如果是"(",就压栈.如果是")"就出栈,
当然,如果栈空的时候出栈,说明 )在( 左边或者是 )的数量高于(,匹配失败,将标志balance位置为假.
当全部遍历完成时,整个栈应该是空的.而且blance标志为真.
from pythonds3 import Stack
def main():
stack = Stack()
balanced = True
'''交互'''
stack_str = input("请输入要判断的括号:")
'''循环判断'''
i = 0
while i<len(stack_str) and balanced:
if stack_str[i] == '(':
stack.push(stack_str[i])
else:
if stack.is_empty():
balanced = False
else:
stack.pop()
i = i + 1
if balanced and stack.is_empty():
print("括号匹配成功!")
else:
print("括号匹配失败!")
3.7 符号匹配
在 Python 中,方括号 [ 和 ] 用于列表, 花括号 { 和 } 用于字典。括号 ( 和 ) 用于元祖和算术表达式。只要每个符号都能保持 自己的开始和结束关系,就可以混合符号。符号字符串如:
{ { ( [ ] [ ] ) } ( ) }
[ [ { { ( ( ) ) } } ] ]
[ ] [ ] [ ] ( ) { }
这些被恰当的匹配了,因为不仅每个开始符号都有对应的结束符号,而且符号的类型也匹 配。
相反这些字符串没法匹配:
( [ ) ]
( ( ( ) ] ) )
[ { ( ) ]
其实我们只需要对刚才的代码进行一个小小的扩展即可实现:
思路: 整体逻辑不变,加入判断函数.
- 当我们执行迭代到某一个右括号时候,出栈.
- 这时如果栈顶的元素(一个左括号)和这个右括号不是匹配的那么将
balance标志置为假. - 因为两个括号夹一个单括号的情况一定是假的.所以不必担心漏掉某些情况
from pythonds3 import Stack
def match(open, close):
opens = "[{("
closes = "]})"
if opens.index(open) == closes.index(close):
return True
def main():
while True:
stack = Stack()
balanced = True
'''交互'''
stack_str = input("请输入要判断的括号:")
'''循环判断'''
i = 0
while i<len(stack_str) and balanced:
if stack_str[i] in '[({':
stack.push(stack_str[i])
else:
if stack.is_empty():
balanced = False
else:
top = stack.pop()
if not match(top, stack_str[i]):
balanced = False
i = i + 1
if balanced and stack.is_empty():
print("括号匹配成功!")
else:
print("括号匹配失败!")
if __name__ == '__main__':
main()
3.8 十进制转换成二进制
我们都知道,对于其他进制转换为十进制的方式就是位权展开,十进制到其他进制的转换就是除模取余。
例如:按位权展开

提取公因子:
1+2*(0+2*(0+2*(1+2*(0+2*(1+2*(1+2* 1)))))))
而除二取余法就可以看成是 位权展开 的 逆运算,也就是一层层拆括号,把余数取出来的过程。而这种相反方向的过程,恰巧可以用栈来实现。
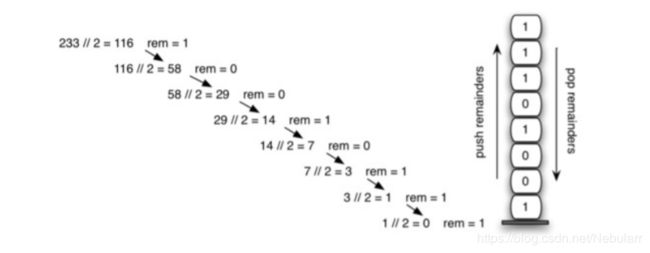
import pythonds3
from pythonds3 import Stack
# 输入一个十进制数字,返回二进制数字
def divideBy2(decNumber):
# 存储余数的栈
dec = decNumber
remstack = Stack()
# 当最后等于零的时候退出
while decNumber > 0 :
rem = decNumber % 2
remstack.push(rem)
decNumber = decNumber // 2
binString = ""
while not remstack.is_empty():
binString += str(remstack.pop())
print("十进制数字{}转换成的二进制数字是{}".format(dec, binString))
return binString
def main():
num = input("请输入一个十进制数字:")
divideBy2(int(num))
if __name__ == '__main__':
main()
from pythonds3 import Stack
# 输入一个十进制数字,返回base进制数字
def baseConverter(decNumber, base):
# 创建一个储存16进制数字的字符串
digits = '0123456789ABCDEF'
dec = decNumber
# 存储余数的栈
remstack = Stack()
# 当最后等于零的时候退出
while decNumber > 0 :
rem = decNumber % base
remstack.push(rem)
decNumber = decNumber // base
newString = ""
while not remstack.is_empty():
newString += digits[remstack.pop()]
print("十进制数字{}转换成的{}进制数字是{}".format(dec, base,newString))
def main():
num1 =input("请输入一个要转换的数字:")
num2 = input("请输入要转换的进制:")
baseConverter(int(num1), int(num2))
if __name__ == '__main__':
main()
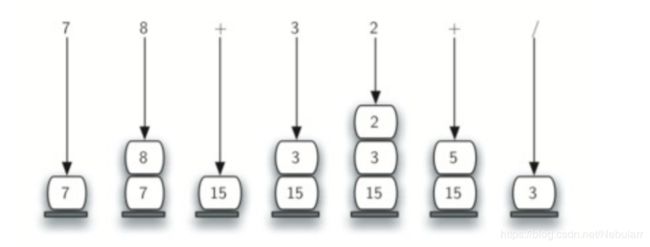
3.9 中缀前缀和后缀表达式
from pythonds.basic.stack import Stack
def infixToPostfix(infixexpr):
prec = {}
prec["*"] = 3
prec["/"] = 3
prec["+"] = 2
prec["-"] = 2
prec["("] = 1
opStack = Stack()
postfixList = []
tokenList = infixexpr.split()
for token in tokenList:
if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":
postfixList.append(token)
elif token == '(':
opStack.push(token)
elif token == ')':
topToken = opStack.pop()
while topToken != '(':
postfixList.append(topToken)
topToken = opStack.pop()
else:
while (not opStack.isEmpty()) and \
(prec[opStack.peek()] >= prec[token]):
postfixList.append(opStack.pop())
opStack.push(token)
while not opStack.isEmpty():
postfixList.append(opStack.pop())
return " ".join(postfixList)
print(infixToPostfix("A * B + C * D"))
print(infixToPostfix("( A + B ) * C - ( D - E ) * ( F + G )"))
from pythonds.basic.stack import Stack
def postfixEval(postfixExpr):
operandStack = Stack()
tokenList = postfixExpr.split()
for token in tokenList:
if token in "0123456789":
operandStack.push(int(token))
else:
operand2 = operandStack.pop()
operand1 = operandStack.pop()
result = doMath(token,operand1,operand2)
operandStack.push(result)
return operandStack.pop()
def doMath(op, op1, op2):
if op == "*":
return op1 * op2
elif op == "/":
return op1 / op2
elif op == "+":
return op1 + op2
else:
return op1 - op2
print(postfixEval('7 8 + 3 2 + /'))
3.10 什么是队列
队列是项的有序集合,其中添加新项的一端称为队尾 ,移除项的一段称为队首.
遵循先进先出FIFO原则
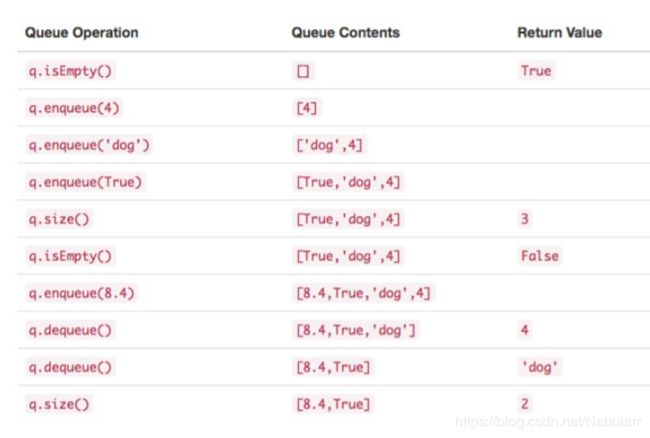
3.11 队列抽象数据类型
- Queue() 创建一个空的新队列。 它不需要参数,并返回一个空队列。
- enqueue(item) 将新项添加到队尾。 它需要 item 作为参数,并不返回任何内容。
- dequeue() 从队首移除项。它不需要参数并返回 item。 队列被修改。
- isEmpty() 查看队列是否为空。它不需要参数,并返回布尔值。
- size() 返回队列中的项数。它不需要参数,并返回一个整数。
3.12 Python实现队列
# from pythonds3 import Queue
#
# q = Queue()
# for i in range(5):
# q.enqueue(i)
# print(q)
#
class Queue:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def enqueue(self, item):
self.items.insert(0, item)
def dequeue(self):
return self.items.pop()
def size(self):
return len(self.items)
3.13 模拟:烫手山芋
约瑟夫问题:一个一世纪著名历史学家弗拉维奥·约瑟夫斯的传奇故事。故事讲的是,他和他的 39 个战友被罗马军队包围在洞中。他们决定宁愿死,也不成为罗马人的奴隶。他们围成一个圈,其中一人被指定为第一个人,顺时针报数到第七人,就将他杀死。约瑟夫斯是一个成功的数学家,他立即想出了应该坐到哪才能成为最后一人。最后,他加入了罗马的一方,而不是杀了自己。
假设拿着山芋的孩子在队列的前面。当拿到山芋的时候,这个孩子将先出列再入队列,把他放在队列的最后。经过 num 次的出队入队后,前面的孩子将被永久移除队列。并且另一个周期开始,继续此过程,直到只剩下一个名字(队列的大小为 1)
from pythonds3 import Queue
def hotPotato(namelist, num):
simqueue = Queue()
for name in namelist:
simqueue.enqueue(name)
while simqueue.size() > 1:
for i in range(num):
simqueue.enqueue(simqueue.dequeue())
simqueue.dequeue()
return simqueue.dequeue()
print(hotPotato([i for i in range(15)], 7))
3.14 模拟:打印机
3.15 什么是Deque
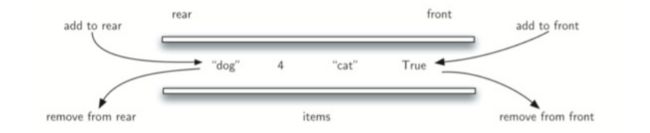
deque(双端队列),两边开口.拥有栈和队列的许多特性.
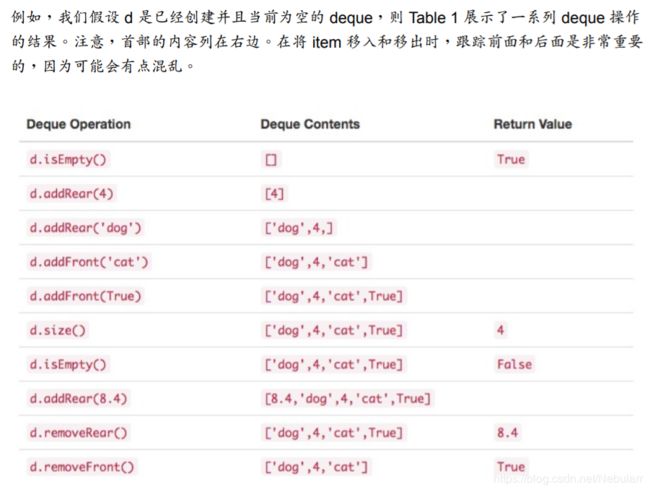
3.16 Deque抽象数据类型
3.17 Python实现Deque
class Deque(object):
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def addFront(self, item):
self.items.append(item)
def addRear(self, item):
self.items.insert(0, item)
def removeFront(self):
return self.items.pop()
def removeRear(self):
return self.items.pop(0)
def size(self):
return len(self.items)
3.18 回文检查
回文串的判定:从头remove一下和从尾remove一下,比较这两个字符是不是相等.最后的剩下的要么是一个元素,要么就是空白的.
from pythonds3 import Deque
def palchecker(aString):
chardeque = Deque()
for ch in aString:
chardeque.add_rear(ch)
stillEqual = True
while chardeque.size() > 1 and stillEqual:
first = chardeque.remove_front()
last = chardeque.remove_rear()
if first != last:
stillEqual = False
return stillEqual
print(palchecker("dsflsdf"))
print(palchecker("radar"))
其实,有句话不知该说不该说.下面的代码同样可以实现…
def palchecker(aString):
return list(aString) == list(aString)[::-1]
3.19 列表
不是所有的语言都有列表这种类型,因此这种概念需要程序员来实现.
列表是项的集合,其中每个项保持相对于其他项的相对位置.称这种类型的列表为无序列表,为了简单起见.我们假设列表不能含有重复项.
3.20 无序列表抽象数据类型
3.21 实现无序列表:链表
为了实现无序列表.需要构造一个链表.
顺序表的构建需要预先知道数据⼤⼩来申请连续的存储空间,⽽在进⾏扩充 时⼜需要进⾏数据的搬迁,所以使⽤起来并不是很灵活。
链表结构可以充分利⽤计算机内存空间,实现灵活的内存动态管理。
注意,必须明确地指定链表的第一项的位置。一旦我们知道第一个项在哪里,第一个项目
可以告诉我们第二个是什么,等等。外部引用通常被称为链表的头。类似地,最后一个项需
要知道没有下一个项.
节点Node类:
节点类主要分两个部分,一部分是数据,一部分是另一个节点的引用。
无序列表类:
class SingleNode(object):
"""单链表的节点"""
def __init__(self, item):
self.item = item
self.next = None
class SingleLinklist(object):
"""定义链表类"""
def __init__(self):
self.__head = None
def is_empty(self):
"""判断是否非空"""
return self.__head == None
def length(self):
"""链表长度"""
cur = self.__head
size = 0
while cur.next != None:
size += 1
cur = cur.next
return size
def travel(self):
"""遍历链表,打印全部节点"""
cur = self.__head
while cur != None:
print(cur.item)
cur = cur.next
def add(self, item):
"""头部添加元素"""
# 先创建一个保存item值的节点
node = SingleNode(item)
# 将新节点的next属性指向head
node.next = self.__head
# 将head指向这个新节点
self.__head = node
def append(self, item):
"""尾部添加元素"""
node = SingleNode(item)
# 先判断是否为空链表,如果为空,则将__head指向新节点
# 如果是空链表,就不可能有next属性
if self.is_empty():
self.__head = node
# 如果不为空列表
cur = self.__head
while cur.next != None:
cur = cur.next
cur.next = node
def insert(self, pos, item):
"""指定位置添加元素"""
# 如果在头节点之前插,则转换为头部插入
if pos <= 0:
self.add(item)
# 如果在尾部之后插,则转换为尾部插入
elif pos > (self.length() - 1):
self.append(item)
else:
node = SingleNode(item)
count = 0
# pre用来指定位置pos的前一个位置pos - 1
pre = self.__head
while count < (pos - 1):
count += 1
pre = pre.next
# 先将新节点的next指向插入位置的节点
node.next = pre.next
# 再把pre指向的节点的next指向新节点
pre.next = node
def remove(self, item):
"""删除节点"""
cur = self.__head
pre = None
while cur != None:
# 找到了指定元素
if cur.item == item:
# 如果第一个就是要删除的节点4
if not pre:
# 将头指针指向头节点的后一个节点
self.__head = cur.next
else:
# 将删除位置前一个节点的next指向删除位置的后一个
pre.next = cur.next
break
else:
# 继续按链表后移节点
pre = cur
cur = cur.next
def search(self, item):
""""查找链表节点是否存在"""
cur = self.__head
while cur != None:
if cur.item == item:
return True
cur = cur.next
return False
if __name__ == "__main__":
ll = SingleLinklist()
ll.add(1)
ll.add(2)
ll.append(3)
ll.insert(6, 4)
print("length:", ll.length())
ll.travel()
print(ll.search(3))
print(ll.search(5))
ll.remove(1)
print("length:", ll.length())
ll.travel()
3.22 有序列表抽象数据结构
顾名思义,其中的数据的顺序是排列好的.排序通常是升序或降序,并且我们假设列表项具有已经定义的有意义的比较运算。许多有序列表操作与无序列表的操作相同。

3.23 实现有序列表

有序列表的 isEmpty 和 size 方法同无序列表, 因为它们不考虑实际项值.
remove也正常工作.只有search和add方法需要一些修改
search 由于是有序的,那么我们搜索到某个节点,若这个节点的值大于我们要搜索的值 而且 之前没有项与要搜索的值匹配. 则判定为未找到.提前结束搜索.
def search(self,item):
current = self.head
found = False
stop = False
while current != None and not found and not stop:
if current.getData() == item:
found = True
else:
if current.getData() > item:
stop = True
else:
current = current.getNext()
return found
add:由于项已经排序,则节点插入位置也会固定.先找到正确的位置,再进行插入.

def add(self,item):
current = self.head
previous = None
stop = False
while current != None and not stop:
if current.getData() > item:
stop = True
else:
previous = current
current = current.getNext()
temp = Node(item)
if previous == None:
temp.setNext(self.head)
self.head = temp
else:
temp.setNext(current)
previous.setNext(temp)
列表的时间复杂度
3.24 总结
- 线性数据结构以有序的方式保存它们的数据。
- 栈是维持 LIFO,后进先出,排序的简单数据结构。
- 栈的基本操作是 push , pop 和isEmpty 。
- 队列是维护 FIFO(先进先出)排序的简单数据结构。
- 队列的基本操作是 enqueue , dequeue 和 isEmpty 。
- 前缀,中缀和后缀都是写表达式的方法。
- 栈对于设计计算解析表达式算法非常有用。
- 栈可以提供反转特性。
- 队列可以帮助构建定时仿真。
- 模拟使用随机数生成器来创建真实情况,并帮助我们回答“假设”类型的问题。
- Deques是允许类似栈和队列的混合行为的数据结构。
- deque 的基本操作是 addFront , addRear , removeFront ,removeRear 和 isEmpty 。
- 列表是项的集合,其中每个项目保存相对位置。
- 链表实现保持逻辑顺序,而不需要物理存储要求。
- 修改链表头是一种特殊情况