机器学习---最大熵模型(MEM)小结
当我们想要得到一个随机事件的概率分布时,如果没有足够的信息来完全确定其概率分布,那么最为保险的方法就是选择一个使得熵最大的分布。
最大熵模型
- 1.信息论知识
- 1.1信息熵的概念
- 1.2.条件熵
- 1.3相对熵
- 1.4互信息
- 1.5几个量之间的关系
- 2.无约束条件
- 3.最大熵原理
- 3.1构造约束条件
- 3.2求解概率分布
1.信息论知识
这里就照搬我写的一篇关于决策树的内容了。原文链接:决策树与随机森林(从入门到精通)
1.1信息熵的概念
设离散型随机变量X的取值有 x 1 , x 2 , x 3 , . . . , x n x_{1},x_{2},x_{3},...,x_{n} x1,x2,x3,...,xn,其发生概率分别为 p 1 , p 2 , p 3 , . . . , p n p_{1},p_{2},p_{3},...,p_{n} p1,p2,p3,...,pn,那么就可以定义信息熵为:
![]()
一般对数的底数是2,当然也可以换成e,当对数底数为2时,信息熵的单位为比特,信息熵也称香农熵。当对数不为2而是其他大于2的整数r时,我们称信息熵为r-进制熵,记为 H r ( X ) H_{r}(X) Hr(X),它与信息熵转换公式为:
![]()
信息熵用以描述信源的不确定度, 概率越大,可能性越大,但是信息量越小,不确定性越小,熵越小。
1.2.条件熵
设随机变量(X,Y)具有联合概率分布:
![]()
条件熵 H ( Y ∣ X ) H(Y|X) H(Y∣X)表示 在已知随机变量X的条件下随机变量Y的不确定性。可以这样理解:(X,Y)发生所包含的熵,减去X单独发生的熵,就是在X发生的前提下,Y发生新带来的熵。
所以条件熵有如下公式成立:
![]()
推导如下:
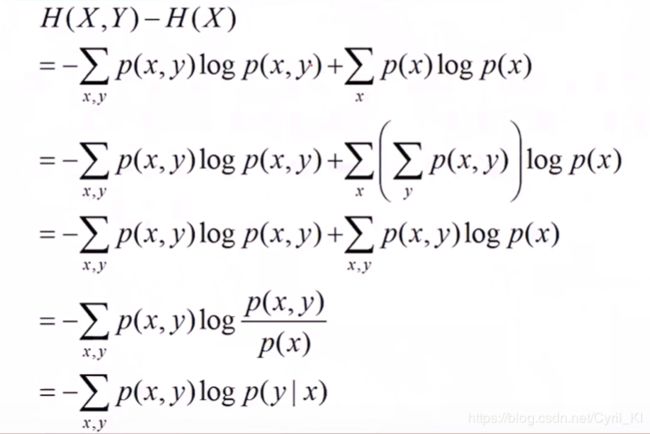
1.3相对熵
相对熵,又称互熵,交叉熵,鉴别信息,Kullback熵,Kullback-Leible散度等。定义如下:
设p(x),q(x)是随机变量X中取值的两个概率分布,则p对q的相对熵为:
![]()
在信息理论中,相对熵等价于两个分布的信息熵(Shannon entropy)的差值。 即:
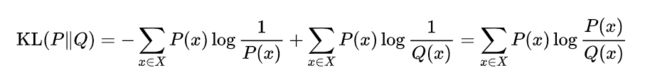
1.4互信息
两个随机变量X和Y的互信息,定义为X,Y的联合分布和独立分布乘积的相对熵。即:
![]()
所以根据KL散度也就是相对熵的定义,可以推出互信息的表达式如下:
![]()
继续推导如下:
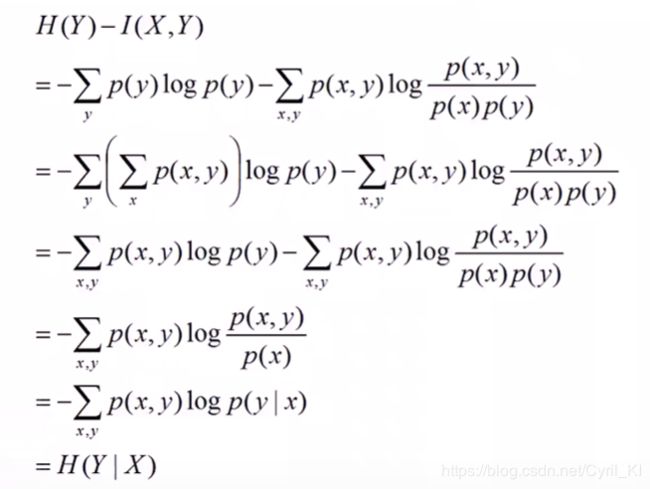
所以最后有:
![]()
1.5几个量之间的关系
结合上述条件熵的两个表达式,可以进一步推出:
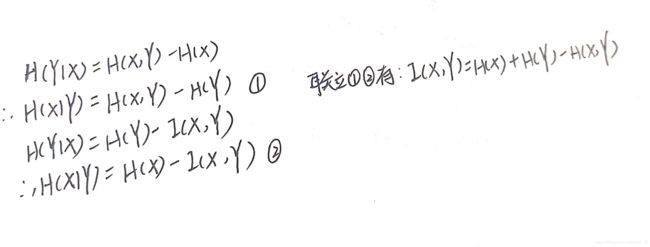
当然我们也可以根据熵的定义来直接推出上面这个互信息的公式:
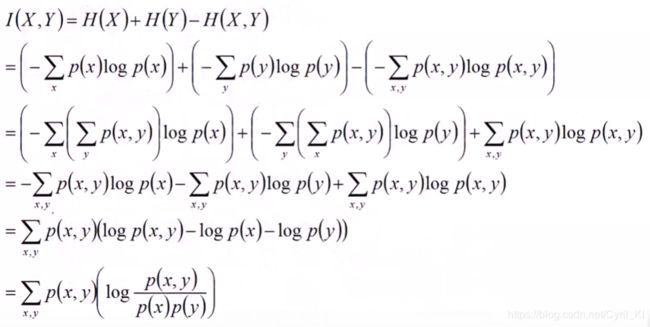
同时我们也可以得到两个不等式:
![]()
上面这个不等式告诉我们,对于一个与X相关的随机变量Y,只要我们得知了一点关于Y的信息,那么X的不确定度就会减小。
最后,借助强大的韦恩图来记住这些关系:
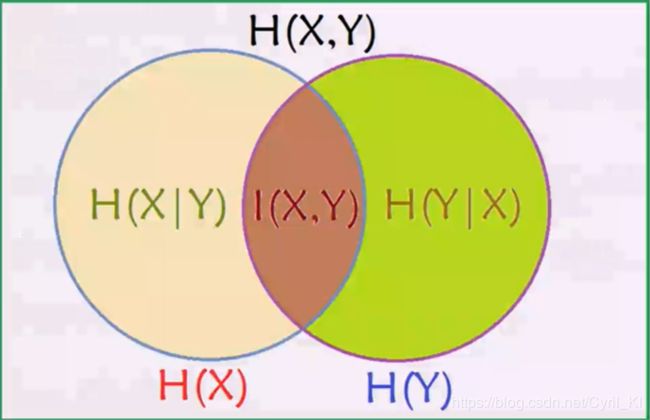
2.无约束条件
假设有一随机变量X是离散的,我们只是知道它有K个可能的取值,其余什么信息都不知道,那么我们该如何估计才能使得熵最大呢?
| X | 1…K |
|---|---|
| p | p1…pK |
根据上面熵的定义,我们知道我们要做的其实就是:
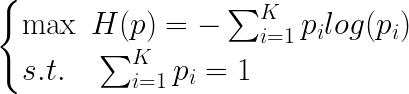
概率相加为1这个条件肯定得是天然满足的,换成求最小值:
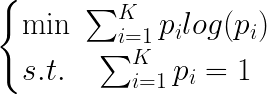
同样利用拉格朗日乘子法,我们令:
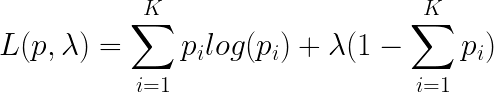
我们让L对 p i p_{i} pi求导得:

可以看到,每一个 p i p_{i} pi都是一个相等的常数,又因为相加为1,所以每一个取值发生的概率都相等并且为1/K。因此,不知道任何已知条件的情况下,离散的随机变量均匀分布时,它的熵最大。
3.最大熵原理
我们设数据集为 ( x 1 , x 2 , . . . , x N ) (x_{1},x_{2},...,x_{N}) (x1,x2,...,xN)。
最大熵原理认为:在所有可能的概率模型中,熵最大的模型为最好的概率模型。求最大熵模型的步骤大致为:
- 根据已知约束条件筛选出可能的概率模型
- 在所有可能的概率模型中选出一个熵最大的模型作为最终的模型。
3.1构造约束条件
我们第一步要根据已知条件筛选出可能的概率模型,那么什么才是已知条件?这个需要我们自己构造,构造步骤如下:
- 我们定义一个f(x),f(x)是任意一个关于随机变量x的函数,我们称它为特征函数。
- 根据我们上面给出的训练数据集,我们可以得到f(x)的经验分布为 p ^ ( f ( x ) ) \hat{p}(f(x)) p^(f(x)),进而求得其经验分布的期望为: E p ^ [ f ( x ) ] E_{\hat{p}}[f(x)] Ep^[f(x)]=一个已知量。
- 解释一下经验分布: p ^ ( f ( x 1 ) ) \hat{p}(f(x1)) p^(f(x1))= x 1 x_{1} x1在训练集中出现的次数/样本集的总数目。
为什么我们要定义一个经验概率分布呢? 因为如果我们判断的随机变量x的概率分布是正确的,那么我们定义一个任意一个特征函数f(x),算出它的经验概率分布的期望,应该就等于f(x)真实的期望,这样我们就构造了一个约束条件。
3.2求解概率分布
其中 δ \delta δ已知。利用拉格朗日乘子法,我们令:

其中 λ 0 是 一 个 常 数 , λ 是 一 个 列 向 量 , \lambda_{0}是一个常数,\lambda是一个列向量, λ0是一个常数,λ是一个列向量,f(x)也是一个列向量,它们都是Q维。我们让L对 p ( x ) p(x) p(x)求导得:
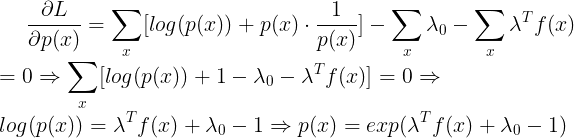 于是我们就得到了 p ( x ) p(x) p(x)的具体值,也就是x的具体分布。剩余参数可以通过KKT条件来求,这里就不再叙述了,具体可以参考:强对偶性、弱对偶性以及KKT条件的证明(对偶问题的几何证明)
于是我们就得到了 p ( x ) p(x) p(x)的具体值,也就是x的具体分布。剩余参数可以通过KKT条件来求,这里就不再叙述了,具体可以参考:强对偶性、弱对偶性以及KKT条件的证明(对偶问题的几何证明)
