前言
基于先前的学习计划,最近打算深入学习Java的集合类,首先要研究的就是HashMap,在学习HashMap前,我花了几天时间温习了一下类中用到的数据结构 (哈希表,二叉树),并决定把所学的知识记录写成文章,本文讲述的就是关于哈希表的知识。
什么是哈希表
在之前的博客文章里,我们简单介绍了数据结构的几种分类,其中就包括哈希表,也称散列表,从根本上来说,一个哈希表包含一个数组,通过特殊的关键码(也就是key)来访问数组中的元素。哈希表的主要思想是通过一个哈希函数, 把关键码映射的位置去寻找存放值的地方 ,读取的时候也是直接通过关键码来找到位置并存进去。
最直接的例子就是字典,例如下面的字典图,如果我们要找 “啊” 这个字,只要根据拼音 “a” 去查找拼音索引,查找 “a” 在字典中的位置 “啊”,这个过程就是哈希函数的作用,用公式来表达就是:f(key),而这样的函数所建立的表就是哈希表。比起数组和链表查找元素时需要遍历整个集合的情况来说,哈希表明显方便和效率的多。

常见的哈希算法
哈希表的组成取决于哈希算法,也就是哈希函数的构成,下面列举几种常见的哈希算法。
1) 直接定址法
- 取关键字或关键字的某个线性函数值为散列地址。
- 即 f(key) = key 或 f(key) = a*key + b,其中a和b为常数。
2) 除留余数法
- 取关键字被某个不大于散列表长度 m 的数 p 求余,得到的作为散列地址。
- 即 f(key) = key % p, p < m。这是最为常见的一种哈希算法。
3) 数字分析法
- 当关键字的位数大于地址的位数,对关键字的各位分布进行分析,选出分布均匀的任意几位作为散列地址。
- 仅适用于所有关键字都已知的情况下,根据实际应用确定要选取的部分,尽量避免发生冲突。
4) 平方取中法
- 先计算出关键字值的平方,然后取平方值中间几位作为散列地址。
- 随机分布的关键字,得到的散列地址也是随机分布的。
5) 随机数法
- 选择一个随机函数,把关键字的随机函数值作为它的哈希值。
- 通常当关键字的长度不等时用这种方法。
哈希冲突
哈希表因为其本身的结构使得查找对应的值变得方便快捷,但也带来了一些问题,以上面的字典图为例,key中的一个拼音对应一个字,那如果字典中有两个字的拼音相同呢?例如,我们要查找 “按” 这个字,根据字母拼音就会跳到 “安” 的位置,这就是典型的哈希冲突问题。这个时候用公式表达就是:
key1 ≠ key2 , f(key1) = f(key2)
一般来说,哈希冲突是无法避免的,如果要完全避免的话,那么就只能一个字典对应一个值的地址,也就是一个字就有一个索引 (安 和 按就是两个索引),这样一来,空间就会增大,甚至内存溢出。
哈希冲突的解决办法
常见的哈希冲突解决办法有两种,开放地址法和链地址法。
一、开放地址法
开发地址法的做法是,当冲突发生时,使用某种探测算法在散列表中寻找下一个空的散列地址,只要散列表足够大,空的散列地址总能找到。按照探测序列的方法,一般将开放地址法区分为线性探查法、二次探查法、双重散列法等。
这里为了更好的展示三种方法的效果,我们用以一个模为8的哈希表为例,采用除留余数法,往表中插入三个关键字分别为26,35,36的记录,分别除8取模后,在表中的位置如下:
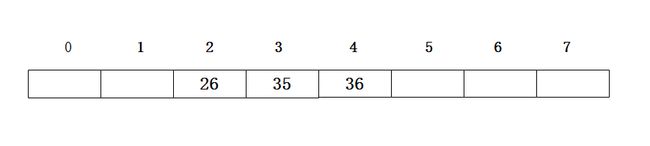
这个时候插入42,那么正常应该在地址为2的位置里,但因为关键字30已经占据了位置,所以就需要解决这个地址冲突的情况,接下来就介绍三种探测方法的原理,并展示效果图。
1) 线性探查法:
fi=(f(key)+i) % m ,0 ≤ i ≤ m-1
探查时从地址 d 开始,首先探查 T[d],然后依次探查 T[d+1],…,直到 T[m-1],此后又循环到 T[0],T[1],…,直到探查到有空余的地址或者到 T[d-1]为止。
插入42时,探查到地址2的位置已经被占据,接着下一个地址3,地址4,直到空位置的地址5,所以39应放入地址为5的位置。
缺点:需要不断处理冲突,无论是存入还是査找效率都会大大降低。
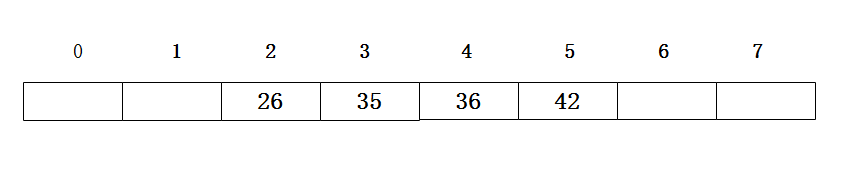
2) 二次探查法
fi=(f(key)+di) % m,0 ≤ i ≤ m-1
探查时从地址 d 开始,首先探查 T[d],然后依次探查 T[d+di],di 为增量序列12,-12,22,-22,……,q2,-q2 且q≤1/2 (m-1) ,直到探查到 有空余地址或者到 T[d-1]为止。
缺点:无法探查到整个散列空间。
所以插入42时,探查到地址2被占据,就会探查T[2+1^2]也就是地址3的位置,被占据后接着探查到地址7,然后插入。

3) 双哈希函数探测法
fi=(f(key)+i*g(key)) % m (i=1,2,……,m-1)
其中,f(key) 和 g(key) 是两个不同的哈希函数,m为哈希表的长度
步骤:
双哈希函数探测法,先用第一个函数 f(key) 对关键码计算哈希地址,一旦产生地址冲突,再用第二个函数 g(key) 确定移动的步长因子,最后通过步长因子序列由探测函数寻找空的哈希地址。
比如,f(key)=a 时产生地址冲突,就计算g(key)=b,则探测的地址序列为 f1=(a+b) mod m,f2=(a+2b) mod m,……,fm-1=(a+(m-1)b) % m,假设 b 为 3,那么关键字42应放在 “5” 的位置。

哈希表性能
哈希表的特性决定了其高效的性能,大多数情况下查找或者插入元素的时间复杂度可以达到O(1), 时间主要花在计算hash值上, 然而也有一些极端的情况,最坏的就是hash值全都映射在同一个地址上,这样哈希表就会退化成链表,例如下面的图片:
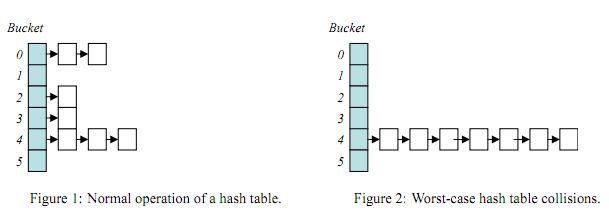
当hash表变成图2的情况时,时间复杂度会变为O(n),效率瞬间低下,所以,设计一个好的哈希表尤其重要,如HashMap在jdk1.8后引入的红黑树结构就很好的解决了这种情况。