无限个无穷小乘积不一定是无穷小(举反例)

有限个无穷小的乘积是无穷小，这个推论书上有证明，不多说，那么无限个无穷小的乘积也是无穷小吗? 我的惯性思维告诉我无限个无穷小相乘应该也是等于无穷小，毕竟无数个接近于0的数（看做无限个小于1的数值相乘）必定是越来越小的，最后结果是无限接近于0。
这样想没有错，但是结论不对。下面会举个反例来反驳一下自己的惯性思维。记录所学

举例之前，先复习几个概念：

1、极限
定义：$\forall$$\epsilon >0$, $\exists \delta >0$, 当 $0<|x-x_0|<\delta$，使$|f(x)-A|<\epsilon$。

• 极限的定义同时也是函数$f(x)$在自变量$x$->$x_0$时极限为$A$的充要条件。
  在没有了解定义之前可能会有些萌，简单的采用数形结合思想便于理解。

• 函数极限在几何上的理解是：在$f(x)$的图像中(例如$y=x$)，找$f(x)$上任意一个连续(取连续是为了让它左右极限都存在，便于说明)的点，这个点$x=x_0$,$f(x_0)=A$。然后回头看定义，进一步描述：

  • 对应的极限的横坐标$x_0$已知，极限函数值A也已知，若是此时任意取$\epsilon$的值(大于0即可)，你动手在图中描一下，发现总能找到这样一个以$x_0$为中心，左右两边的长度都为$\delta$的自变量小区间，即存在这个去心邻域U($x_0$ , $\delta$)。在这个区间中，自变量对应的函数值$f(x)$跟极限值$f(x)=A$的距离一定是在$\epsilon$之内。此为对极限定义的具体描述。

  PS : 对任意$\epsilon >0$是为了体现$\epsilon$的任意小，通过约束$f(x)$离函数极限值A不断靠近的距离来约束$x$向$x_0$不断的逼近，来模拟在这一点的极限过程。如果在任意$\epsilon >0$情况下，能找到最少一个满足条件的$\delta$存在才能算此极限成立，找不到这样一个$\delta$,那么只能说函数$f(x)$在$x-x_0$时极限为A是不成立的。

2、无穷小
定义：是指函数f(x)当$x$->$x_0$(或者$x$->$\infty$)时，极限为0，那么称函数$f(x)$为当$x$->$x_0$(或者$x$->$\infty$)时的无穷小。
PS：无穷小的本质是函数，一种满足在自变量趋于某点时极限A为0的函数。所以本质上无穷小也是极限内容，可以用极限来定义来证明：$\forall$$\epsilon >0$, $\exists \delta >0$, 当 $0<|x-x_0|<\delta$，使$|f(x)|<\epsilon$。

举反例：

有无限多个函数公式如下（皆为分段函数）：
$$f(x{)}_1\{\begin{array}{ll}100,& x\ge 1\\ x,& 0<x<1\\ -x,& -1<x<0\\ 100,& x\le -1\end{array}$$
$$f(x{)}_2\{\begin{array}{ll}100,& x\ge 1/2\\ x,& 0<x<1/2\\ -x,& -1/2<x<0\\ 100,& x\le -1/2\end{array}$$
$$f(x{)}_3\{\begin{array}{ll}100,& x\ge 1/3\\ x,& 0<x<1/3\\ -x,& -1/3<x<0\\ 100,& x\le -1/3\end{array}$$

、、、、、、 、、、、、、 、、省略、、 、、、、、、 、、、、、、

$$f(x{)}_n\{\begin{array}{ll}100,& x\ge 1/n\\ x,& 0<x<1/n\\ -x,& -1/n<x<0\\ 100,& x\le -1/n\end{array}$$

、、、、、、 、、、、、、 省略无限多个 、、、、、、 、、、、、、

---

每个$f(x)n$的图像大概是这个样子的，

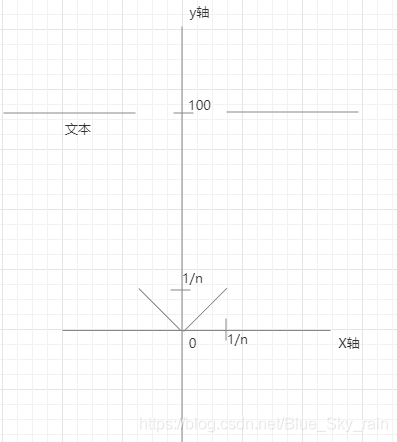
可以看出每一个函数发$f(x{)}_n$在$x$->$0$的时候都有极限0。所以每个函数$f(x{)}_n$都可以称为各自在$x$->$0$的无穷小。

我们设无限多个无穷小相乘：$F(x)=f(x{)}_1\ast f(x{)}_2\ast f(x{)}_3......\ast f(x{)}_n....\ast f(x{)}_k......$

根据极限值为0的定义（看做无穷小的定义），对于$\forall$$\epsilon >0$, $\exists \delta >0$, 当 $0<|x-x_0|<\delta$，使$|F(x)|<\epsilon$成立。

证明$F(x)$是在$x$->$x_0$的无穷小：先设$\epsilon =M>0$，$M$就是确定值，你会发现无论区间$(x_0-\delta )U(x_0+\delta )$范围缩小多么小，从中选取自变量x=1/k总会有从乘数$f(x{)}_k$开始$x=1/k$的时候，对应的函数值$f(1/k{)}_k$是100，往后的$f(x{)}_k$${}_{+}$${}_1$,$f(x{)}_k$${}_{+}$${}_2$,$f(x{)}_k$${}_{+}$${}_3$…这些乘数对应函数值都是100，共有无数个100相乘。而在$f(x{)}_k$之前的乘数的值即使再小，也只是有限个(k个)非常小的数相乘。无数个100与有限个非常小的数相乘，乘积$F(x)$会是非常非常大的值，必然导致出现$|F(x)|>M$,也就是说你找不到这样一个$\delta$存在，使定义成立，故$F(x)$是在$x$->$x_0$的无穷小不成立。
在这个例子当中只要自变量$x\ne 0$，后面必然都会出现无数个100的情况，最后的乘积都是一个无穷大的值。
由此说明无限多个无穷小乘积是无穷小这句话不对。

结束

---

---

---

数列
数列是序列的子集，什么是序列呢？序列是一个包含其他对象的有序集合，它是有次序的，比如一个字符串就是一个序列，每个字符对应都有索引，是有序的。数列属于序列的一种，那么数列也是有次序的，数列的元素都是数值，对应的每个位置上都是确定的数值，亦或者说每个数值都有确定的位置。
书上对于数列的概念感觉模棱两可，说是实数$x_n$按照下标n从小到排列得到的序列叫数列，我一度认为一定能写出通项表达式才能叫数列。其实则不然，像字符串不就是没有公式表示出来吗，但它确确实实是按照字符串内容每个字符有先后顺序的序列，比如i love you,you 跟 i 要是位置反过来意思就不一样。同样我们把π的每一个数字按照先后也写成一个数列，同样满足按照某种规则有序排列，但是通项公式好像也写不出来，或者说很难找的到。
我一直相信这个世界上的所有一切都有迹可循，所谓万法自然也不过是遵照某种模式在运行，他们的本质具体抽象出来就是一堆数学公式加上各种参数。不然你说算命算卦的为什么不叫看命读褂的，偏偏叫“算”命的（我在瞎扯别理我O(∩_∩)O哈哈~），因为其中纷繁复杂，不能一言堪破，需要去算，凡算必然牵扯到数学。所以我“断言”古代那些神机妙算的人都是数学天才！是能堪破命理，让一个人和国家的命运变得直观清晰的数学集大成者。但是这样很难，因为得足够聪明。现在的算命的十有八九是骗人的神棍，信则有不信则无的东西虚无缥缈被说中了一两件也证明不了什么。真要有那个智商，被骗怪我我智不如人，我都服气。据说在明朝有个神机妙算的刘伯温，是朱元璋的打天下时求来的得力谋士，它为朱元璋献的计谋屡屡扭转局势，为大明夺得天下立下赫赫战功。被后人广为传颂是它的神机妙算，这里面还包含很多典故，比如早年一句恭维朱元璋的话“皇城这么雄伟大概只有燕子才能飞的进来”，恰好后面燕王朱棣造反，令人渍渍称奇。我觉得他如果真的会算那么一定是对天下命理有独有自己的一套研究，说不定家里床底下藏着一本《500年后的五百年后公式大全》(*￣︶￣)，啊，我明白了（豁然开朗），他是穿越的，我早已洞察一切简直机智的一批 ，但是通过它晚年的下场很不好，被朱元璋排挤，最后怎么走的历史都没记载，可怜的刘susu。也不知是不是他真的神机妙"算"，如果是，那他是否算出自己晚年不幸呢？天道无常啊，卦不可算尽。

---