【连载】计算机组成原理 --- 第二章数据的表示和运算

本节内容主要分为：

（一）：数制与编码

    1：进位计数制及其相互转换；真值和机器数

    2：BCD码；字符与字符串；校验码

（二）：定点数的表示和运算

    1：定点数的表示

    有无符号数的表示

    2：定点数的运算

    定点数的移位运算，原码定点数的加减运算；补码定点数的加减运算

    定点数的乘除运算，溢出概念和判定方法

（三）：浮点数的表示和运算

    1：浮点数的表示

    2：浮点数的加减运算

（四）：算术逻辑单元ALU

    1：串行加法器和并行加法器

    2：算术逻辑单元ALU的功能和结构

2.1：数制与编码

2.1.1 进位计数制及其相互转换

    可以参考这篇 https://wenku.baidu.com/view/15f3b4826529647d26285205.html

2.1.2真值和机器数

    在计算机中，通常采用数的符号和数值一起编码的方法来表示数据，常用的有原码，补码，反码表示法。这种把符号“数字化”的数 称为机器数。

2.1.3BCD码

    二进制编码的十进制数（Binary-Coded Decimal，BCD）通常采用4位二进制数来表示一位十进制数中的0~9这10个数码。但2^4 = 16 - 10= 6， 其有6种状态为冗余状态。

    8421码：

    8421码又称为BCD码，是十进制代码中最常用的一种。在这种编码方式中，每一位二值代码的“1”都代表一个固定数值。将每位“1”所代表的二进制数加起来就可以得到它所代表的十进制数码。因为代码中从左至右看每一位“1”分别代表数字“8”“4”“2”“1”，故得名8421码。其中每一位“1”代表的十进制数称为这一位的权。因为每位的权都是固定不变的，所以8421码是恒权码。

2.1.4字符与字符串

     计算机内部只能识别和处理二进制代码，所以字符都必须按照一定的规则用一组二进制编码来表示。

     在 ASCII 编码中，一个英文字母字符存储需要1个字节。在 GB 2312 编码或GBK 编码中，一个汉字字符存储需要2个字节。在UTF-8编码中，一个英文字母字符存储需要1个字节，一个汉字字符储存需要3到4个字节。

     字符串的存放：一种常用的表示法是使用一个字符代码的数组，每个字符占用一个字节（如在ASCII代码中）或两个字节（如在unicode中）。它的长度可以使用一个结束符（一般是NUL，ASCII代码是0，在C编程语言中使用这种方法）。

2.1.5奇偶校验码

    奇偶校验位（英语：parity bit）或校验比特（英语：check bit）是一个表示给定位数的二进制数中1的个数是奇数还是偶数的二进制数。奇偶校验位是最简单的错误检测码。

奇偶校验位有两种类型：偶校验位与奇校验位。

    如果一组给定数据位中1的个数是奇数，那么偶校验位就置为1，从而使得1的个数是偶数。如果给定一组数据位中1的个数是偶数，那么奇校验位就置为1，使得总的1的个数是奇数。

7位数据 （1的个数）	带有校验位的字节
	偶校验位	奇校验位
0000000（0）	00000000	00000001
1010001（3）	10100011	10100010
1101001（4）	11010010	11010011
1111111（7）	11111111	11111110

 

2.2定点数的表示与运算:

2.2.1：定点数的表示

1：机器数的表示方法：

       机器数的表示方法一共有两种：定点表示法和浮点表示法。

定点表示法

定点，就是指小数点的位置保持不变。小数点要么放在最高位之前，要么放在最低位之后，前一种就是定点小数的表示方法，后面一种就是定点整数的表示方法。在计算机中，定点数有四种表示方法：原码、反码、补码和移码。。。

原码

最高位用来表示符号：0代表正数，1代表负数。剩下的全部用来表示这个数的绝对值。。。

例如： x=-110，则x[原]=1110；x=110，则x[原]=0110
注意：对于原码表示方法，0的表示方法有两种：+0:0000，-0:1000。。。

反码

我们在原码的基础上来理解反码吧。。。
最高位用来表示符号：0代表正数，1代表负数。正数的反码和原码的表示方法一样，负数的反码是除了符号位之外，其他位全部取反。。。
例如：x=-110，则x[反]=1001；x=110，则x[反]=0110
注意：和原码表示方法一样，0的反码的表示方法也有两种：+0:0000，-0:1111。。。

补码

最高位用来表示符号：0代表正数，1代表负数。正数的补码和原码的表示方法一样，负数的补码是在反码的基础上+1得到的。。。
例如：x=-110，则x[补]=1001；x=110，则x[补]=0111
注意：和原码以及反码不一样的是：0的表示方法只有一种。。。
补充：还有一种求解一个负数的补码的方法：就是在正数的补码表示上，从右到左寻找第一个1，然后将1左边的数字全部取反。。。

移码

和上述三种表示方法不一样：最高位的0代表负数，1代表正数。要得到一个数的移码也很简单，知道将它的补码形式的符号位取反即可。。。
例如：x=-110，则x[移]=0001；x=110，则x[移]=1111
注意：和补码一样，0的表示方法也只有一种。。。

---

浮点表示法

浮点，指小数点的位置会浮动，一般用来表示小数。按照位数的不同，常见的浮点数可以分成两种，32位的单精度浮点数，64位的双精度浮点数。当然，在实际的计算机中，还有其他类型的，下面主要对单精度进行谈论，双精度的知识与单精度的类似。。。

单精度

S占一位，表示正负，0为正，1为负。。。
Exponent占8位（双精度浮点数中占11位），表示指数部分。大小为实际指数的大小加上偏移量127（双精度的偏移量大小为1203）。。。
Fraction占23位（双精度浮点数中占52位），表示小数部分。需要注意的是，需要先将数字进行规格化，即装换成1.******的形式。然后，只需要将小数点后面的部分进行存储就可以了，因为除了零之外的其他数的第一位都是1。。。

下面的例子演示如何将一个真值转换成浮点数：

2.2.2定点数的运算

    1：定点数的移位运算

    有两种移位方式，逻辑移位和算数移位。下面以一个8位二进制数1000 1011为例来探讨。

逻辑移位：

把1000 1011视为一串二进制串，不对该串做任何解读，不管是原码还是补码还是别的什么，只管移位，移丢了就移丢了，多出来的空位一律补0。1000 1011逻辑左移一位成为0001 0110，逻辑右移一位成为0100 0101。

算数移位:

算数移位本质上是为了实现有符号数的快速乘除法。算数移位想要达到的效果是：使得算数左移一位得到的结果是原数乘以2(在最高位没有溢出的情况下)，使得算数右移一位得到的结果是原数除以2(忽略移丢的最低位)。

原码、反码、补码的编码规则各不相同，在不同的编码规则下要达到同样的最终效果，那就必须对10001011这一串数字作出解读，根据这串数字的编码规则而采用不同的移位策略。

为了达到上述目的，显然应该规定“无论左移还是右移，符号位是不应该因移位改变的”。那么剩下的工作就是看看移位之后空出来的位置应该补0还是应该补1。

先看最简单的原码表示法。若1000 1011B是一个原码，则它表示的是-11D，算数左移时，符号位为1不变，其余位000 1011依次左移，最高位的0移丢了(移丢的是0，所以没有溢出，若此处移丢的是1，则溢出，结果出错)，最低位空出来一位，若最低位补0，则最终结果为1001 0110B，表示-22D，就是将-11乘以2的结果。

(此处的道理可参考王道论坛《2012计算机组成原理 联考复习指导》2.2节，再看看唐朔飞《计算机组成原理》第二版P235表6.5和6.6，相信一切就很清楚了。)

同样的道理，以此类推，可总结如下：

有符号数为正数时，原码、反码、补码的空位皆补0，因为它们对于正数的编码是相同的。

有符号数为负数时

原码左移、原码右移得到的空位均补0

反码左移、反码右移得到的空位均补1
补码左移得到的空位补1，补码右移得到的空位补0

要注意区分正负数，比如整数补码的右移空位补0，而负数右移空位补1。

参考http://www.cnblogs.com/ybwang/archive/2011/10/26/2225034.html

2.3浮点数表示法

    在计算机科学中，浮点（英语：floating point，缩写为FP）是一种对于实数的近似值数值表现法，由一个有效数字（即尾数）加上幂数来表示，通常是乘以某个基数的整数次指数得到。以这种表示法表示的数值，称为浮点数（floating-pointnumber）。利用浮点进行运算，称为浮点计算，这种运算通常伴随着因为无法精确表示而进行的近似或舍入。     

1 浮点数的表示
通常，我们可以用下面的格式来表示浮点数

S

P

M

2:浮点数的运算：

其中S是符号设两个浮点数X=Mx*2Ex ，Y=My*2Ey

实现X±Y要用如下5步完成：
（1）对阶操作：小阶向大阶看齐
（2）进行尾数加减运算
（3）规格化处理：尾数进行运算的结果必须变成规格化的浮点数，对于双符号位（就是使用00表示正数，11表示负数，01表示上溢出，10表示下溢出）的补码尾数来说，就必须是001×××…×× 或110×××…××的形式
若不符合上述形式要进行左规或右规处理。
（4）舍入操作：在执行对阶或右规操作时常用“0”舍“1”入法将右移出去的尾数数值进行舍入，以确保精度。
（5）判结果的正确性：即检查阶码是否溢出
若阶码下溢（移码表示是00…0），要置结果为机器0；
若阶码上溢（超过了阶码表示的最大值）置溢出标志。位，P是阶码，M是尾数。

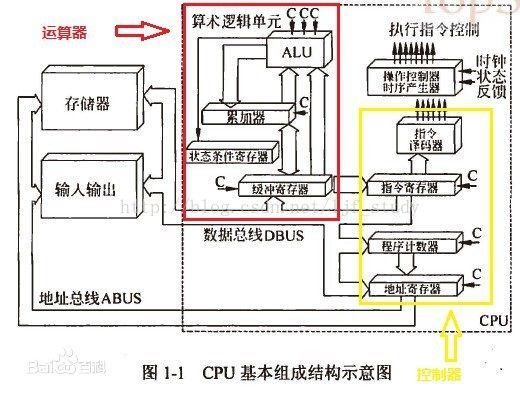
2.4算术逻辑单元ALU

在计算机中，运算器承担了执行各种算术和逻辑运算的工作，运算器由算术逻辑单元ALU，累加器，状态寄存器和通用寄存器等组成。ALU的基本功能包括加减乘除四则运算。与或非异或等逻辑运算，以及移位，求补等操作。