一个简单的3层神经网络模型part1

背景知识要求

Python基础
Pandas库基础
Matplotlib库基础
机器学习-神经网络基础知识

摘要

运用一个3层神经网络训练上一篇文章“链家房源数据清洗和预处理(pandas)”https://blog.csdn.net/qq_39206674/article/details/90114819中清理出来的数据。
通过训练数据判断一个房子是满5年、满2年、或者非满2满5年。
使用精度、准确率、召回率、AUC等指标对神经网络模型进行评价。

正文

拆分训练集、交叉验证集和测试集

从csv文件读入数据，将数据集分为训练集、交叉验证集和测试集。

import pandas as pd


pd.set_option('display.max_columns', 1000)
# pd.set_option('display.width', 1000)
# pd.set_option('display.max_colwidth', 1000)

# 读文件
df = pd.read_csv(r'lianjia_processed.csv', sep=',')

# 查看数据
print(df.head(3))
print("processed data rowCount: %d" % (df.shape[0]))
print("training set size should be %d: " % (df.shape[0]*60/100))
print("validation set size should be %d: " % (df.shape[0]*20/100))
print("test set size should be %d: " % (df.shape[0]*20/100))

# 分割数据集
sep_train = int(df.shape[0]*60/100)
sep_valid = int(df.shape[0]*60/100) + int(df.shape[0]*20/100)
sep_test = int(df.shape[0]*60/100) + int(df.shape[0]*20/100) + int(df.shape[0]*20/100)

df[0:sep_train].to_csv("./trainset/training_data.csv", index=False)
df[sep_train:sep_valid].to_csv("./validset/validation_data.csv", index=False)
df[sep_valid:sep_test].to_csv("./testset/test_data.csv", index=False)

print("3 kinds data set create succeed!")

加载训练集、交叉验证集、测试集数据

将df[“is_two_five”]列（房龄是否满2或满5）作为目标值，该列数值取值范围为{0,2,5}，分别表示非满2满5年，满两年，满五年。通过二值化将该列拆分为3列数据，对应0列{0：非满2满5，1：满2或满5}，对应1列{0：非满2, 1：满2}，对应2列{0：非满5， 1：满5}。

import numpy as np
import pandas as pd


def loadTrainSet():
    df = pd.read_csv(r'./trainset/training_data.csv', sep=',')

    TempY = df["is_two_five"].values
    Y = np.array([TempY, TempY, TempY])
    Y[0, :][Y[0, :] == 0] = 1
    Y[0, :][Y[0, :] != 1] = 0
    Y[1, :][Y[1, :] == 2] = 1
    Y[1, :][Y[1, :] != 1] = 0
    Y[2, :][Y[2, :] == 5] = 1
    Y[2, :][Y[2, :] != 1] = 0

    df.drop("is_two_five", axis=1, inplace=True)
    X = df.values
    return X, Y


def loadValidSet():
    df = pd.read_csv(r'./validset/validation_data.csv', sep=',')

    TempY = df["is_two_five"].values
    Y = np.array([TempY, TempY, TempY])
    Y[0, :][Y[0, :] == 0] = 1
    Y[0, :][Y[0, :] != 1] = 0
    Y[1, :][Y[1, :] == 2] = 1
    Y[1, :][Y[1, :] != 1] = 0
    Y[2, :][Y[2, :] == 5] = 1
    Y[2, :][Y[2, :] != 1] = 0

    df.drop("is_two_five", axis=1, inplace=True)
    X = df.values
    return X, Y


def loadTestSet():
    df = pd.read_csv(r'./testset/test_data.csv', sep=',')

    TempY = df["is_two_five"].values
    Y = np.array([TempY, TempY, TempY])
    Y[0, :][Y[0, :] == 0] = 1
    Y[0, :][Y[0, :] != 1] = 0
    Y[1, :][Y[1, :] == 2] = 1
    Y[1, :][Y[1, :] != 1] = 0
    Y[2, :][Y[2, :] == 5] = 1
    Y[2, :][Y[2, :] != 1] = 0

    df.drop("is_two_five", axis=1, inplace=True)
    X = df.values
    return X, Y

3层神经网络模型

参考了Andrew Ng的神经网络模型,隐藏层激励函数为tanh，输出层激励函数为sigmoid，输入层12个神经元，输出层3个神经元，超参数为隐藏层神经元数量n_h和学习率learning_rate，使用梯度下降法和反向传播计算损失函数的代价，代码如下：

#!/usr/bin/env Python
# coding=utf-8
import numpy as np


def sigmoid(x):
    """
    Compute the sigmoid of x

    Arguments:
    x -- A scalar or numpy array of any size.

    Return:
    s -- sigmoid(x)
    """
    s = 1/(1+np.exp(-x))
    return s


def layer_sizes(X, Y):
    """
    Arguments:
    X -- input dataset of shape (input size, number of examples)
    Y -- labels of shape (output size, number of examples)
    
    Returns:
    n_x -- the size of the input layer
    n_y -- the size of the output layer
    """
    n_x = X.shape[0]  # size of input layer
    n_y = Y.shape[0]  # size of output layer
    return (n_x, n_y)


def initialize_parameters(n_x, n_h, n_y):
    """
    Argument:
    n_x -- size of the input layer
    n_h -- size of the hidden layer
    n_y -- size of the output layer

    Returns:
    params -- python dictionary containing your parameters:
                    W1 -- weight matrix of shape (n_h, n_x)
                    b1 -- bias vector of shape (n_h, 1)
                    W2 -- weight matrix of shape (n_y, n_h)
                    b2 -- bias vector of shape (n_y, 1)
    """

    np.random.seed(1)  # we set up a seed so that your output matches ours although the initialization is random.

    W1 = np.random.randn(n_h, n_x) * 0.01
    b1 = np.zeros((n_h, 1))
    W2 = np.random.randn(n_y, n_h) * 0.01
    b2 = np.zeros((n_y, 1))

    assert (W1.shape == (n_h, n_x))
    assert (b1.shape == (n_h, 1))
    assert (W2.shape == (n_y, n_h))
    assert (b2.shape == (n_y, 1))

    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}

    return parameters


def forward_propagation(X, parameters):
    """
    Argument:
    X -- input data of size (n_x, m)
    parameters -- python dictionary containing your parameters (output of initialization function)

    Returns:
    A2 -- The sigmoid output of the second activation
    cache -- a dictionary containing "Z1", "A1", "Z2" and "A2"
    """
    # Retrieve each parameter from the dictionary "parameters"
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    # Implement Forward Propagation to calculate A2 (probabilities)
    Z1 = np.dot(W1, X)+b1
    A1 = np.tanh(Z1)
    Z2 = np.dot(W2, A1)+b2
    A2 = sigmoid(Z2)

    assert(A2.shape == (3, X.shape[1]))

    cache = {"Z1": Z1,
             "A1": A1,
             "Z2": Z2,
             "A2": A2}

    return A2, cache


def compute_cost(A2, Y, parameters):
    """
    Computes the cross-entropy cost given in equation (13)

    Arguments:
    A2 -- The sigmoid output of the second activation, of shape (1, number of examples)
    Y -- "true" labels vector of shape (1, number of examples)
    parameters -- python dictionary containing your parameters W1, b1, W2 and b2

    Returns:
    cost -- cross-entropy cost given equation (13)
    """

    m = Y.shape[1]  # number of example

    # Compute the cross-entropy cost
    logprobs = np.multiply(np.log(A2), Y) + np.multiply(np.log(1-A2), 1-Y)
    cost = - np.sum(logprobs)/m

    cost = np.squeeze(cost)     # makes sure cost is the dimension we expect.
                                # E.g., turns [[17]] into 17
    assert(isinstance(cost, float))

    return cost


def backward_propagation(parameters, cache, X, Y):
    """
    Implement the backward propagation using the instructions above.

    Arguments:
    parameters -- python dictionary containing our parameters
    cache -- a dictionary containing "Z1", "A1", "Z2" and "A2".
    X -- input data of shape (2, number of examples)
    Y -- "true" labels vector of shape (1, number of examples)

    Returns:
    grads -- python dictionary containing your gradients with respect to different parameters
    """
    m = X.shape[1]

    # First, retrieve W1 and W2 from the dictionary "parameters".
    W1 = parameters["W1"]
    W2 = parameters["W2"]

    # Retrieve also A1 and A2 from dictionary "cache".
    A1 = cache["A1"]
    A2 = cache["A2"]

    # Backward propagation: calculate dW1, db1, dW2, db2.
    dZ2 = A2-Y
    dW2 = np.dot(dZ2, A1.T)/m
    db2 = np.sum(dZ2, axis=1, keepdims=True)/m
    dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2))
    dW1 = np.dot(dZ1, X.T)/m
    db1 = np.sum(dZ1, axis=1, keepdims=True)/m

    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}

    return grads


def update_parameters(parameters, grads, learning_rate=0.005):
    """
    Updates parameters using the gradient descent update rule given above

    Arguments:
    parameters -- python dictionary containing your parameters
    grads -- python dictionary containing your gradients

    Returns:
    parameters -- python dictionary containing your updated parameters
    """
    # Retrieve each parameter from the dictionary "parameters"
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]

    # Retrieve each gradient from the dictionary "grads"
    dW1 = grads["dW1"]
    db1 = grads["db1"]
    dW2 = grads["dW2"]
    db2 = grads["db2"]

    # Update rule for each parameter
    W1 = W1-learning_rate*dW1
    b1 = b1-learning_rate*db1
    W2 = W2-learning_rate*dW2
    b2 = b2-learning_rate*db2

    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}

    return parameters


def nn_model(X, Y, n_h, num_iterations=10000, print_cost=False, learning_rate=0.0005):
    """
    Arguments:
    X -- dataset of shape (2, number of examples)
    Y -- labels of shape (1, number of examples)
    n_h -- size of the hidden layer
    num_iterations -- Number of iterations in gradient descent loop
    print_cost -- if True, print the cost every 1000 iterations

    Returns:
    parameters -- parameters learnt by the model. They can then be used to predict.
    """

    np.random.seed(3)
    n_x = layer_sizes(X, Y)[0]
    n_y = layer_sizes(X, Y)[1]

    # Initialize parameters, then retrieve W1, b1, W2, b2. Inputs: "n_x, n_h, n_y". Outputs = "W1, b1, W2, b2, parameters".
    parameters = initialize_parameters(n_x, n_h, n_y)
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]

    # Loop (gradient descent)

    for i in range(0, num_iterations):

        #print(i)
        # Forward propagation. Inputs: "X, parameters". Outputs: "A2, cache".
        A2, cache = forward_propagation(X, parameters)

        # Cost function. Inputs: "A2, Y, parameters". Outputs: "cost".
        cost = compute_cost(A2, Y, parameters)

        # Back propagation. Inputs: "parameters, cache, X, Y". Outputs: "grads".
        grads = backward_propagation(parameters, cache, X, Y)

        # Gradient descent parameter update. Inputs: "parameters, grads". Outputs: "parameters".
        parameters = update_parameters(parameters, grads, learning_rate=learning_rate)

        # Print the cost every 10 iterations
        if print_cost and i % 500 == 0:
            print ("Cost after iteration %i: %f" %(i, cost))

    return parameters


def predict(parameters, X):
    """
    Using the learned parameters, predicts a class for each example in X

    Arguments:
    parameters -- python dictionary containing your parameters
    X -- input data of size (n_x, m)

    Returns
    predictions -- vector of predictions of our model (red: 0 / blue: 1)
    """

    # Computes probabilities using forward propagation, and classifies to 0/1 using 0.5 as the threshold.
    A2, cache = forward_propagation(X, parameters)
    # predictions = (A2 > 0.5)


    return A2

训练模型并验证

#!/usr/bin/env Python
# coding=utf-8
import time
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, fbeta_score
from sklearn.metrics import roc_curve, auc
from Layer3NN import nn_model
from Layer3NN import predict
from loadDataset import loadTrainSet
from loadDataset import loadValidSet
from loadDataset import loadTestSet


def normalize(X):
    """Min-Max normalization     sklearn.preprocess 的MaxMinScalar
    Args:
        X: 样本集
    Returns:
        归一化后的样本集
    """
    m, n = X.shape
    # 归一化每一个特征
    for j in range(n):
        features = X[:, j]
        minVal = features.min(axis=0)
        maxVal = features.max(axis=0)
        diff = maxVal - minVal
        if diff != 0:
           X[:, j] = (features-minVal)/diff
        else:
           X[:, j] = 0
    return X


# 模型超参数调整
n_h = 10
iter_num = 170000
learning_rate = 0.1

# 模型参数训练
time_start = time.time()
rawTrainX, trainY = loadTrainSet()
trainX = normalize(rawTrainX)

print(trainX.shape)
print(trainY.shape)
parameters = nn_model(trainX.T, trainY, n_h, num_iterations=iter_num, print_cost=True, learning_rate=learning_rate)

time_end = time.time()
print('totally time cost', time_end-time_start)

# 模型结果预测-训练集
predictTrainSet = predict(parameters, trainX.T)

# 模型评价-训练集
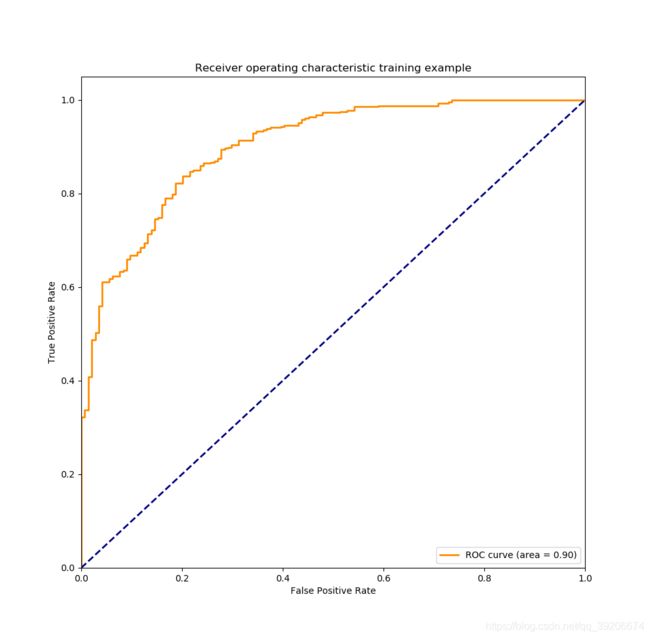
fpr_tr, tpr_tr, threshold_tr = roc_curve(trainY[2, :], predictTrainSet[2, :])  # 计算真正率和假正率
roc_auc = auc(fpr_tr, tpr_tr)  # 计算auc的值
lw = 2
plt.figure(figsize=(10, 10))
plt.plot(fpr_tr, tpr_tr, color='darkorange', lw=lw, label='ROC curve (area = %0.2f)' % roc_auc)  # 假正率为横坐标，真正率为纵坐标做曲线
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic training example')
plt.legend(loc="lower right")
plt.show()

print('TrainSet Accuracy: %.3f' % accuracy_score(y_true=trainY[2, :], y_pred=predictTrainSet[2, :] > 0.5))
print('TrainSet Precision: %.3f' % precision_score(y_true=trainY[2, :], y_pred=predictTrainSet[2, :] > 0.5))
print('TrainSet Recall: %.3f' % recall_score(y_true=trainY[2, :], y_pred=predictTrainSet[2, :] > 0.5))
print('TrainSet F1: %.3f' % f1_score(y_true=trainY[2, :], y_pred=predictTrainSet[2, :] > 0.5))
print('TrainSet F_beta: %.3f' % fbeta_score(y_true=trainY[2, :], y_pred=predictTrainSet[2, :] > 0.5, beta=0.8))

# 模型结果预测-交叉验证集
rawValidX, validY = loadValidSet()
validX = normalize(rawValidX)
predictValidSet = predict(parameters, validX.T)

# 模型评价-交叉验证集
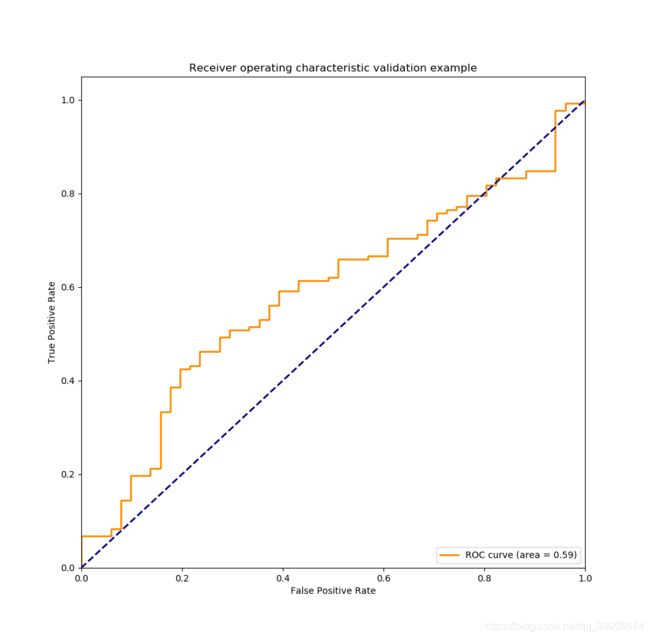
fpr_va, tpr_va, threshold_va = roc_curve(validY[2, :], predictValidSet[2, :])  # 计算真正率和假正率
roc_auc = auc(fpr_va, tpr_va)  # 计算auc的值
lw = 2
plt.figure(figsize=(10, 10))
plt.plot(fpr_va, tpr_va, color='darkorange', lw=lw, label='ROC curve (area = %0.2f)' % roc_auc)  # 假正率为横坐标，真正率为纵坐标做曲线
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic validation example')
plt.legend(loc="lower right")
plt.show()

print('ValidSet Accuracy: %.3f' % accuracy_score(y_true=validY[2, :], y_pred=predictValidSet[2, :] > 0.5))
print('ValidSet Precision: %.3f' % precision_score(y_true=validY[2, :], y_pred=predictValidSet[2, :] > 0.5))
print('ValidSet Recall: %.3f' % recall_score(y_true=validY[2, :], y_pred=predictValidSet[2, :] > 0.5))
print('ValidSet F1: %.3f' % f1_score(y_true=validY[2, :], y_pred=predictValidSet[2, :] > 0.5))
print('ValidSet F_beta: %.3f' % fbeta_score(y_true=validY[2, :], y_pred=predictValidSet[2, :] > 0.5, beta=0.8))
pass

运行结果一

参数如下:
隐藏层神经元数量 n_h = 10
迭代次数 iter_num = 170000
学习率 learning_rate = 0.1
运行结果：

Cost after iteration 169500: 0.876729
totally time cost 278.90972542762756
TrainSet Accuracy: 0.853
TrainSet Precision: 0.884
TrainSet Recall: 0.921
TrainSet F1: 0.902
TrainSet F_beta: 0.898
ValidSet Accuracy: 0.683
ValidSet Precision: 0.718
ValidSet Recall: 0.924
ValidSet F1: 0.808
ValidSet F_beta: 0.786

训练集AUC：

测试集AUC：

运行结果二

参数如下:
隐藏层神经元数量 n_h = 10
迭代次数 iter_num = 300000
学习率 learning_rate = 0.05
运行结果：
训练集测试结果：

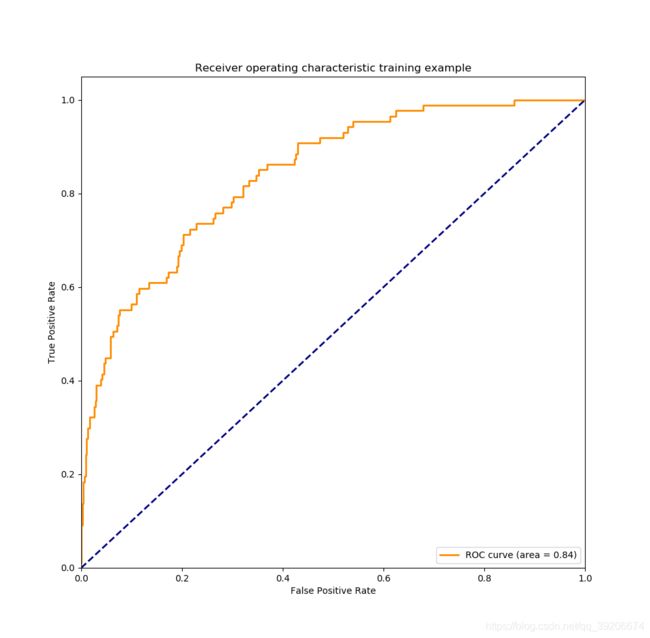
验证集测试结果：

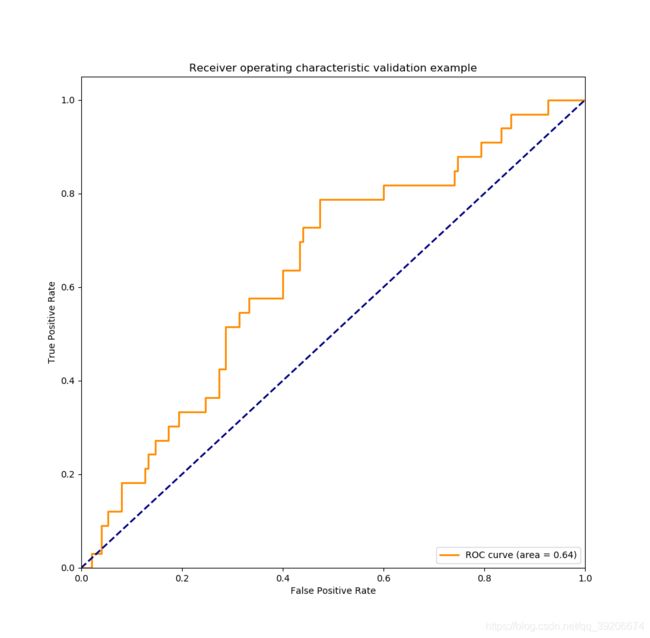
运行结果三

修改隐藏层数量为6、8、12，运行结果更差。

结论

1、训练集的精度明显高于验证集的精度，说明模型存的bias或variance问题。
2、AUC的结果表明，模型在验证集的泛化结果很差。
后续将从几个角度对增加模型的训练效果：
1 从特征工程的角度，改善特征质量。
例如：本文rawTrainX和rawValidX通过normlize()函数分别处理，然而SKlearn.preprocess预处理方法是，使用fit_transform处理训练集和然后使用训练集fit的参数直接用transform验证集的数据。
2 引入sklearn的K-fold验证，增加模型验证的有效性，并定位模型是high bias问题还是high variance问题
3 解决high bias问题或higvariace问题。

参考

1. Andrew Ng 机器学习。
2. 分类器的不同的性能评价指标https://blog.csdn.net/winycg/article/details/80378847