感知机原理剖析笔记(如何理解感知机)——《统计学习方法》 李航
文章目录
- 感知机
- 感知机模型
- 感知机学习策略
- 感知机学习算法
- 原始形式
- 对偶形式
感知机
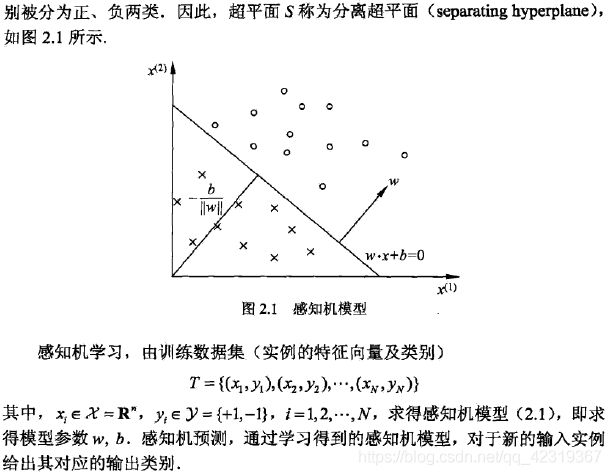
感知机(perceptron)是二分类的线性分类模型,输入为实例的特征向量,输出为实例的类别,取+1和-1二值。感知机对应于输入空间(特征空间)中将实例分为正负两类的分离超平面。属于判别模型。感知机的学习训练过程旨在寻找一个超平面,能够将实例进行线性划分,为此,我们要导入误分类的损失函数,利用随机梯度下降法对损失函数进行最小化,求取感知机模型。
感知机学习算法具有简单而易于实现的优点,分为原始形式和对偶形式。感知机1957年由Rosenblatt提出,是神经网络和支持向量机的基础。
感知机模型
在这里,详细介绍一下超平面,他不同于我们一般意义上的平面,他可以是多维度的,在二维平面上,我们可以将其看成一条直线;在三维空间中,我们可以将其看成一个平面;在更高的维度(n维)中,它的维度为n-1维。
从超平面的表达公式中,我们可以看出
ω ⋅ x + b = 0 \omega \cdot x+b=0 ω⋅x+b=0
\omega 为向量,超平面的公式符合多变量的线性回归模型,这也从侧面上说明了超平面不可能为 “ 曲面 ”。
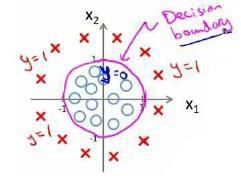
就像上面的这张图,我们通过一个紫色的圆将●和×分离开,但是我们的超平面就是这个在二维平面中的圆圈,根据我们之前讲的,它肯定不是,既然不是,那么我们应该如何去将这个平面给找出来,这个时候我们就需要去进行升维,因为维度越高,我们所获得的信息也越高,我们从三维空间中去看该图中数据实例的分布,可能是这样的
这样我们就能够确定出超平面,完美将实例进行划分。
但我们会产生这样的疑问,如果实例在三维空间中的真实分布为×包围●的球体咋办?
这时候,我们在三维中获取的信息已经不能够将实例给完美线性分割,这时候我们需要继续升维,但超过三维,已经很难去想象它的几何分布了,但事实证明,只要我们不断升维就一定能够找到将实例线性分割的超平面。
感知机学习策略
感知机的学习策略简单的说就是通过定义损失函数,不断迭代求解函数系数,来使得损失函数最小化。
损失函数的选取也需要注意,一个最简单的策略是选取误分类点的总数,但该方法损失函数的系数不连续可导,一个更优的策略是计算误分类点到超平面的距离,优化距离以最小。
1 ∥ ω ∥ ∣ ω ⋅ x 0 + b ∣ \frac{1}{\left \| \omega \right \|}\left | \omega \cdot x_{0}+b\right | ∥ω∥1∣ω⋅x0+b∣
上面的公式表示,数据点x0到超平面的距离,\omega 为超平面的法向量,b为偏置。
为啥会是这个公式?刚开始我也不是太明白,后来我查询了一些资料,对该公式进行了推导。详细如下:
(1)证明了 \omega 为法向量,(2)证明了上述的距离公式
由于误分类点一定满足公式
− y i ( ω ⋅ x i + b ) > 0 -y_{i}(\omega \cdot x_{i}+b)>0 −yi(ω⋅xi+b)>0
所以该公式可以作为对数据点类型的判断标准
结合距离公式,并对所有误分类点距离求和,可以得到损失函数
L ( ω , b ) = − ∑ x ∈ M y i ( ω ⋅ x i + b ) L(\omega ,b)=-\sum_{x\in M}^{}y_{i}(\omega \cdot x_{i}+b) L(ω,b)=−x∈M∑yi(ω⋅xi+b)
M为误分类点的集合
损失函数为非负函数,函数值为0时,表示完全分类正确;函数值越小,表示划分越准确。
感知机学习算法
原始形式
上述过程,为感知机学习算法的学习过程。
选取\omega和b的初值,选取误分类点,代入,对损失函数的系数求偏导并更新系数,详细如下图
如此反复循环,直至不存在误分类点或者误分类点尽量少。
例题:
对偶形式


感知机学习算法的对偶形式与原始形式相似,这里简单说一下两者的不同之处。
不同的一点为,将 \omega 和 b 用训练过程中的总增量进行表示。
另一个需要注意的是,对偶形式中训练实例仅以内积的形式从出现,可以为了后续的计算方便,将实例间的内积提前计算出来并以矩阵的形式存储,这个矩阵叫做Gram矩阵。