yalmip求解鲁棒优化

前言

记录一下早期夭折的研究想法，想使用鲁棒优化（robust optimization，RO）解决整数变量的资源分配问题。目标函数和约束条件都很简单， 但是含有随机变量。由于随机变量的分布未知，在此考虑使用鲁棒优化RO进行资源分配，具有更好地鲁棒性，即对变化具有更好包容性。如果能够得到随机变量的均值和方差，使用鲁棒优化资源分配十分完美。
但是对于随机变量，自己又没有实际的数据，无法得到其均值和方差，也无从进行数据拟合，进行概率分布检验（卡方检验等）。最终的想法也就夭折了。或许夭折的想法也有意义，在此记录，以便对看到的人有启发。

鲁棒优化简介

鲁棒优化是含有不确定参数的优化问题 [1]，同随机优化不同。随机优化的不确定参数是具有确定性概率分布的随机变量。而鲁棒优化的不确定性，是指在优化问题中相关不确定参数位于确定的集合范围内，没有确定的概率分布，这里的参数可以是目标函数的系数，也可以是约束条件的系数。鲁棒优化追求即便是在最坏情况下（worst case）,其得出的解仍然满足约束条件，不可违背。
鲁棒优化对于数学功底好的同学来说，写论文很顺畅。因为鲁棒优化一般都可以转换为确定性的对等式（Robust counterpart），再使用确定的求解方法求解。

yalmip

yalmip类似python的第三方库，在MATLAB环境下运行，支持多种优化求解器，使得求解优化问题十分简单方便。使用yalmip求解鲁棒优化参考[2]，yalmip的使用可以参考[3]。

实操求解

优化问题

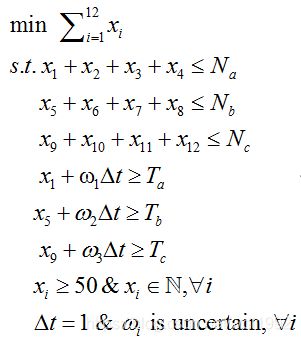
示例优化问题如上图所示，12个整数优化变量，3个不确定参数。在该示例中，假设不确定集合为box类型（即箱型，每个不确定参数都有确定上下界）。以上示例可以很简单的转化为确定性的线性规划问题。

示例代码

%% 2019-7-1 by WDL
% 使用鲁棒优化建模分析
% 定义整数变量 包含优化变量和随机变量
clc;clear all
%step1 变量定义
x = intvar(12, 1);%优化变量 intvar定义整型优化变量12行1列
w = intvar(3, 1);%随机变量
%step2 参数设置 
Ta=150; Tb=150; Tc=150;  
Na=400;Nb=400;Nc=400;
dt=1;%时间间隔

%添加约束条件
 F = [x(1)+x(2)+x(3)+x(4)<=Na,...
     x(5)+x(6)+x(7)+x(8)<=Nb,...
     x(9)+x(10)+x(11)+x(12)<=Nc,... %约束条件（1）-（3）
     x(1)>=w(1)*dt+Ta>=0,...
     x(5)>=w(2)*dt+Tb>=0,...
     x(9)>=w(3)*dt+Tc>=0,...%约束条件（4）-（6）
     x>=50]; %非负约束
%设置不确定集合，此示例为box类型 
% W = [0<=w(1)<=40,0<=w(2)<=40,0<=w(3)<=40,uncertain(w)];
 W = [-20<=w<=20,uncertain(w)]; %uncertain(w)指明不确定性
 options = sdpsettings('solver','cplex');   %设置求解器为cplex
 objective = sum(x); %目标函数 最小化优化变量累加和
 sol=optimize(F + W,objective,options) %优化求解
 Xc=value(x) %解
 Oc=value(objective)%目标值
 

 %% 不考虑鲁棒优化
 x=intvar(12,1);
 F1 = [x(1)+x(2)+x(3)+x(4)<=Na,...
     x(5)+x(6)+x(7)+x(8)<=Nb,...
     x(9)+x(10)+x(11)+x(12)<=Nc,... %约束条件（1）-（3）
     x(1)>=w(1)*dt+Ta>=0,...
     x(5)>=w(2)*dt+Tb>=0,...
     x(9)>=w(3)*dt+Tc>=0,...%约束条件（4）-（6）
     x>=50]; %非负约束
 objective1 = sum(x);
 options = sdpsettings('solver','cplex');   %设置求解器为cplex
 sol1=optimize(F1,objective1,options)
 Xc1=value(x) 
 Oc1=value(objective1)
 
figure %作图
X=[Xc,Xc1]
bar3(X)

结果

(1)鲁棒优化
Oc=960
Xc=[170 50 50 50 170 50 50 50 170 50 50 50]’
(1)确定性优化
Oc1=600
Xc1=[50 50 50 50 50 50 50 50 50 50 50 50]’

总结

使用yalmip时，最好安装相应的求解器，例如cplex或者gurobi。

参考文献
[1] Gorissen, Bram L., et al. “A Practical Guide to Robust Optimization.” Omega-International Journal of Management Science, vol. 53, 2015, pp. 124–137.
[2]Robust optimization. https://yalmip.github.io/tutorial/robustoptimization/
[3]yalmip + lpsolve + matlab 求解混合整数线性规划问题（MIP/MILP）. https://www.cnblogs.com/kane1990/p/3428129.html