机器学习基础 第三章 分类算法

1 线性分类器-感知器

1.1 感知器

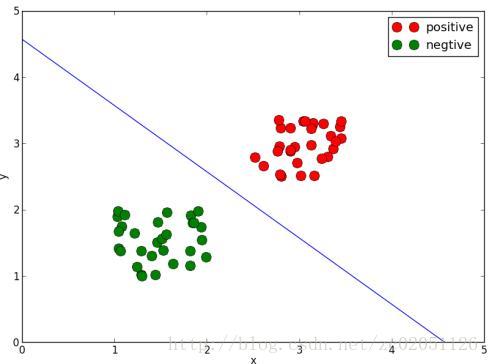
有如图1.1所示的两类数据希望找到，如果想把他们分开，最简单的方法就是用图中的绿线将它们分开。显然绿线的方程为

t=ω0+ω1x+ω1y−−−−−（1.1−1）

假设红色点为 {xr,yr} ，绿色点的集合为 {xg,yg} ，则红色和绿色点分别满足

t≥0,t<0−−−−−（1.1−2）

所以只要能求出式（1-1）并按照式（1-2）的规则就能将两类数据分开，将以上的想法表示成如下形式，可以称之为感知器

f(t)=sign(ω0+ω1x+ω1y )−−−−−（1.1−3）

sign 为符号函数

sign(x)={+1, x≥0−1,x<0 −−−−−（1.1−4）

图1. 1

假设样本集合为 {xi,yi;ti} ， 1≤i≤N ， N 为样本总数。

1.2 感知器的学习策略

和回归模型一样，感知器也要进行学习，才能获取感知器的参数 ω ，所以也需要构造损失函数。

图1.1中的直线称为分类线，如果数据是高维的，则线就会变成超平面了。在这里为了找到这条分类线，这条线需要满足这样的准则（损失函数）：即线两边的点被误分的总数要最少，图1.1中所示的情况下，误分的总数为0。这样的损失函数不是参数 ω 的连续可导函数，不容易优化，所以下面引入另一种损失函数。

对于误分类来说，有

−t(ω0+ω1x+ω1y)>0−−−−−（1.2−2）

这是因为， ω0+ω1x+ω1y>0 时， t=−1 ，反之亦然。因此将样本点中所有符合式（1.2-2）的样本点累加作为损失函数，并使其最小，就可以确定 ω ，损失函数如下

E(ω)=−∑i=1Mti(ω0+ω1xi+ω1yi)−−−−−（1.2−3）

其中的 M 为 N 个样本中被误分样本的个数。当式（1.2-3）为0时，全部样本分类正确。

1.3 优化损失函数

根据第二部分介绍的梯度下降法，需要求解损失函数的偏导数，式（1.2-3）可以直接求出偏导数而不用数值导数的求法

∂E(ω)∂ω0=−∑i=1Mti

∂E(ω)∂ω1=−∑i=1Mtixi

∂E(ω)∂ω2=−∑i=1Mtiyi

（1.3-1）

则

ω0=ω0−λ∂E(ω)∂ω0

ω1=ω1−λ∂E(ω)∂ω1

ω2=ω2−λ∂E(ω)∂ω2

（1.3-2）

这里给出另一种类似梯度下降法的优化方法：随机梯度下降法（《Pattern Recognition And Machine Learning》M.
Bishop一书中感知机一节中的解释），随机梯度下降法不对整个样本集合求导数，而对单个样本就导数，所以式（1.3-2）变成

ω0=ω0+λti

ω1=ω1+λtixi

ω2=ω2+λtiyi

最终的优化流程如下：

假设训练样本为 {xi,yi;ti} ， 1≤i≤N ， N 为样本总数

（1）选取初值 ω0,ω1,ω2
（2）在训练集 {xi,yi;ti} 中选择 (xi,yi;ti)

（3）如果 −ti(ω0+ω1xi+ω1yi)>0 ，则更新：

ω0=ω0+λti

ω1=ω1+λtixi

ω2=ω2+λtiyi

（4）转到（2）直到训练集合中没有误分点

1.4 代码实现

第一步：生成训练数据集

def twoSamples(n = 30):
    x = []
    y = []
    x.extend([[1.0 + random.random(), 1.0 + random.random()] for i in xrange(n)])
    x.extend([[2.5 + random.random(), 2.5 + random.random()] for i in xrange(n)])
    y.extend([-1 for i in xrange(n)])
    y.extend([1 for i in xrange(n)])
    return [x, y]

第二步：随机梯度下降法优化目标函数

def perSGD(x, y):
    w0 = np.array([0.1, 0.1])
    b0 = 0.1
    lamda = 0.1
    while 1:
        k = 0
        for i in xrange(len(x)):
            xi = x[i]
            yi = y[i]
            if yi * (w0[0] * xi[0] + w0[1] * xi[1] + b0) <= 0.0:
                w0 = w0 + lamda * yi * w0
                b0 = b0 + lamda * yi
                k = k + 1
        if k == 0:
            break
    return w0, b0

第三步：画出分类线

def plotDL(x, y, w, b):
    px = [0.0, -b/w[1]]
    py = [-b/w[0], 0.0]
    x = np.array(x)
    y = np.array(y)
    plt.plot(x[y == 1, :][:,0], x[y == 1, :][:,1], 'ro', markersize = 12)
    plt.plot(x[y == -1, :][:,0], x[y == -1, :][:,1], 'go', markersize = 12)
    plt.plot(px, py)
    plt.legend(('positive','negtive'))
    plt.xlim([0, 5])
    plt.ylim([0, 5])
    plt.xlabel('x')
    plt.ylabel('y')
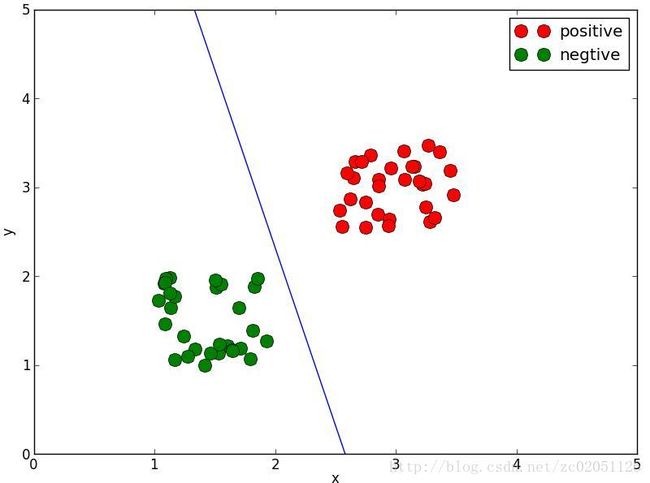
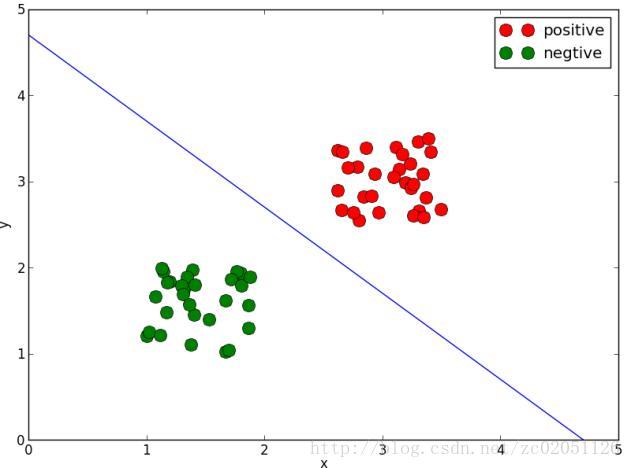
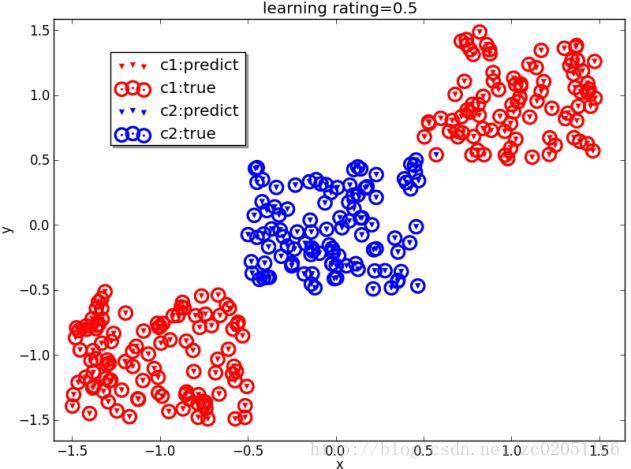
    plt.show()

用上面的程序计算的两幅图如下

（a） ω0=0.1,ω1=0.2,ω2=0.8

（b） ω0=0.1,ω1=0.2,ω2=0.2
图1.4.1 不同参数时的分类线

图1.4.1说明感知器对参数的初始值比较敏感，不同的初值得到不同的分类线。这也是感知器的缺点

2 线性分类器-逻辑回归

2.1 逻辑回归分布

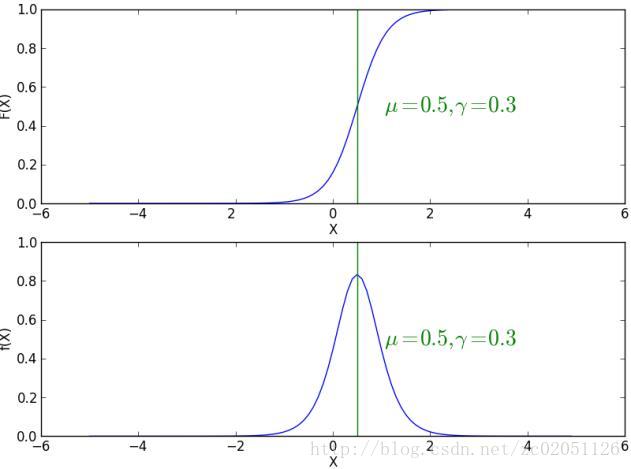
定义：设 X 为连续随机变量， X 服从逻辑分布是指 X 具有如下分布函数和概率密度函数

F(x)=P(X≤x)=11+e−(x−μ)γ−−−−−（2.1−1）

f(x)=F′(x)=e−(x−μ)γγ(1+e−(x−μ)γ)2−−−−−（2.1−2）

其中， μ 为位置参数， γ>0 为形状参数。

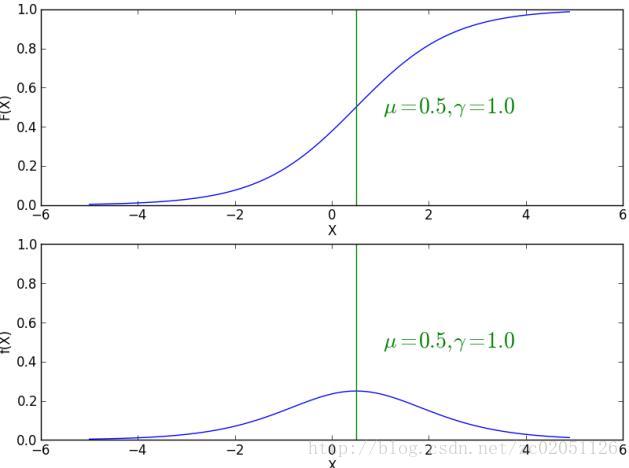
下图是不用 γ 参数下的两幅分布图和概率密度图

图 2.1.1 不同参数 γ 时的分布图和概率密度图

F(x) 满足

F(−x+μ)−12=−F(x−μ)+12−−−−−（2.1−2）

F(x) 对称中心为 (μ,12) ，随着 γ 变小 F(x) 在对称中心处变化率变大， f(x) 变得尖锐。

2.2 二项逻辑回归

二项逻辑回归模型是一种分类模型，由条件概率 P(Y|X) 表示，这里随机变量 X 取值为实数，随机变量 Y 取0或者1，通过监督学习方法学习模型参数。二项逻辑回归的条件概率分布如下

P(Y=1|x)=e(ω1∙x+ω0)1+e(ω1∙x+ω0)−−−−−（2.2−1）

P(Y=0|x)=11+e(ω1∙x+ω0)−−−−−（2.2−2）

这里 x∈Rn ， Y∈{0,1} ， ω1∈Rn 称为权向量， ω0∈R 称为偏置， ω1∙x 称为 ω1 与 x 的内积。

分类时只要计算天健概率 P(Y=1|x) 和 P(Y=0|x) 哪个条件概率大，样本 x 就属于哪一类。

2.3 参数估计

逻辑回归模型学习时，对于给定的训练集合

{xi,yi}，1≤i≤N，x∈Rn，yi∈{0,1}

，可以用极大似然法估计模型的参数。按照极大似然估计的似然函数的定义，逻辑回归的似然函数为

L=∏i=1NP(xi,yi)=∏i=1NP(yi|xi)P(xi)−−−−−（2.3−1）

因为 P(xi) 是已知的量，所以似然函数可以省略掉 P(xi) ，似然函数为

L=∏i=1NP(xi,yi)=∏i=1NP(yi|xi)P(xi)≡∏i=1NP(yi|xi)−−−−−（2.3−2）

P(yi|xi)=[P(Y=1|xi)]yi[1−P(Y=1|xi)]1−yi−−−−−（2.3−3）

对数似然函数为

log(L)≡log∏i=1N[P(Y=1|xi)]yi[1−P(Y=1|xi)]1−yi=∑i=1Nyilog{P(Y=1|xi)}+(1−yi)log{[1−P(Y=1|xi)]}−−−−−（2.3−4）

按照极大似然估计理论，只要极大化对数自然函数，就可以估计出模型参数，等价于极小化负的对数似然函数，所以最优化方法最终的目标函数为

L¯=−∑i=1Nyilog{P(Y=1|xi)}+(1−yi)log{[1−P(Y=1|xi)]}−−−−−（2.3−5）

式（2.3-5）的梯度为

∇L¯=∑i=1N[P(Y=1|xi)−yi]xi−−−−−（2.3−6）

只要按照下式迭代计算参数 ω ，当梯度 ∇L¯ 满足一定的精度时，迭代结束，求得最终的最优参数 ω

ω=ω−λ∇L¯−−−−−（2.3−7）

其中， λ 为学习率（步长）。

2.4 基函数

和回归中的类似，分类中也能够引入基函数，在特征空间上对特征进行变换。只要将对数似然函数中的特征变量 xi 加上基函数 ϕ(x) ， ϕn= ϕ(xn) ，式（2.3-5）和式（2.3-6）分别变为

L¯=−∑i=1Nyilog{P(Y=1|ϕ(xi))}+(1−yi)log{[1−P(Y=1|ϕ(xi))]}−−−−−（2.3−8）

式（2.3-5）的梯度为

∇L¯=∑i=1N[P(Y=1|ϕ(xi))−yi]ϕ(xi)−−−−−（2.3−9）

2.5 过拟合（正则化）

为了解决过拟合问题，需要将式（2.3-8）加上一项罚项，变为

L^=L¯+α2∑i=1Mω2i−−−−−（2.3−10）

∇L^=∑i=1N[P(Y=1|ϕ(xi))−yi]ϕ(xi)+αω−−−−−（2.3−11）

ω=ω−λ(∇L¯+αω)−−−−−（2.3−12）

2.6 参数的矩阵表示

省略推导过程，给出带有基函数和正则项情况下的参数 ω 的矩阵表示

ω=(ΦTΦ+αI)−1ΦTy−−−−−（2.3−13）

其中

Φ=⎡⎣⎢⎢⎢⎢⎢11⋮1ϕ(x1)ϕ(x2)⋮ϕ(xN)⎤⎦⎥⎥⎥⎥⎥

Φ 是 N×(M+1) 维的矩阵

2.7 代码实现

此节代码全部在softmax.py中，鉴于代码较多就不在文档中体现了。Softmax算法是逻辑回归的推广，即可以实现多分类的逻辑回归，详细的理论见http://deeplearning.stanford.edu/wiki/index.php/Softmax%E5%9B%9E%E5%BD%92。

Softmax.py中的类Softmax类有如下初始化参数：

算法的学习率： alfa（double）
算法的罚参数： lamda（double）
训练数据中的特征个数：feature_num（int）
训练数据中的类别数目：label_mum（int）
是否使用核函数： kernel （bool）
训练模型时的运行次数：run_times = 500
训练模型时的收敛阈值： col = 1e-6

其中的train方法，接受两个参数，第一个为训练数据的特征，第二个参数为训练数据对应的标签

Predict方法接受一个参数为预测数据的特征，返回的结果为每个样本的分类结果。

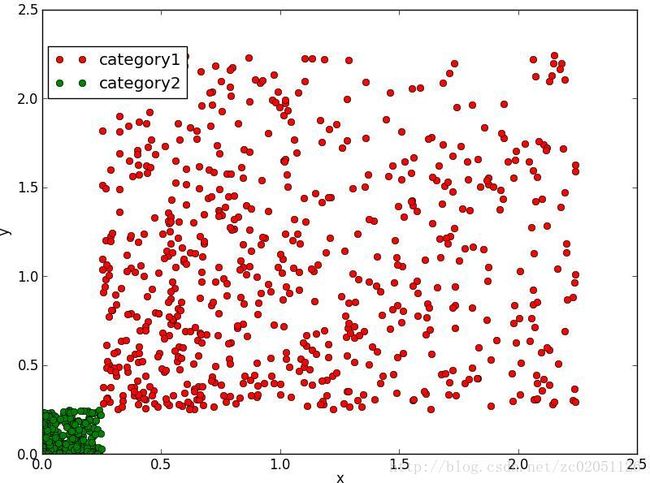
图2.7.1中，（a）所示的数据是不可分的，（b）中显示了误分类的情况，（c）中展示了对图（a）中引入了基函数 x2 后的结果，显然图（c）中的数据是可分的了，分类结果见图（d）。

（a）原始的两类数据

（b）没用核函数的二分类结果

（c）加入基函数变换后的数据

（d）加入基函数后的分类结果
图2.7.1 二分类逻辑回归问题

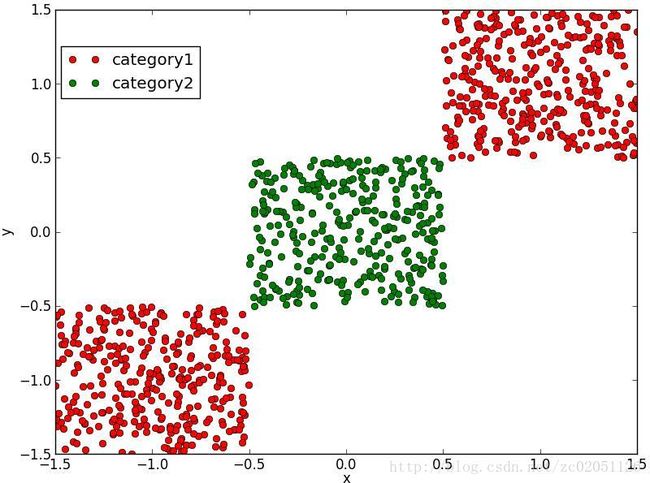
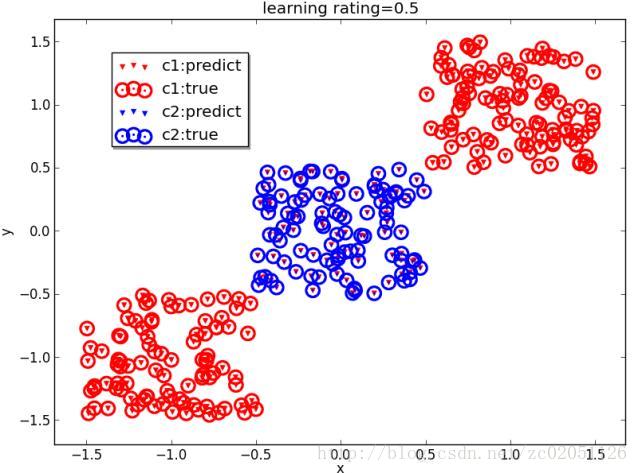
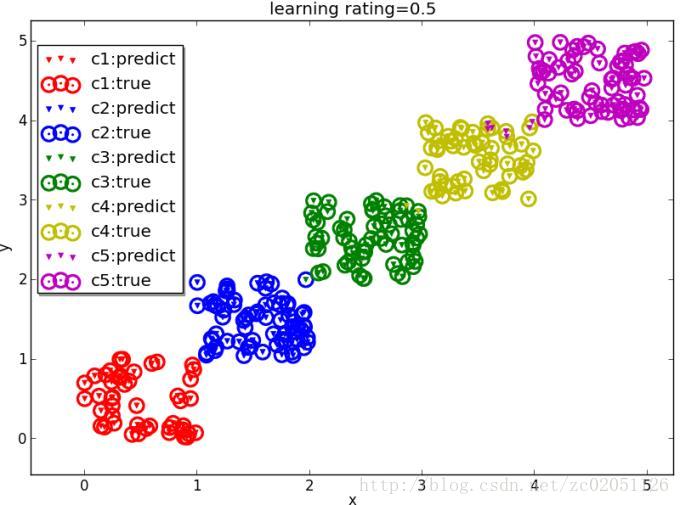
图2.7.2是softmax对多分类的结果

图2.7.2 softmax多分类结果

3 贝叶斯分类器

贝叶斯分类器，是最常用也是性能不错的分类器。其可以分为：基于高斯分布的贝叶斯分类器，主要对连续变量进行分类；多项式贝叶斯分类器，主要处理离散变量，如对文本的分类就是这种；贝努力贝叶斯分类器，主要处理二元样本。

3.1 贝叶斯公式

概率论里的贝叶斯公式如下

p(y|x)=p(x|y)p(y)p(x)−−−−−（3.1−1）

如果把 y 当成类别，把 x 当成样本，则式（5.1-1）可写为

p(类别∣∣样本)=p(样本∣∣类别)p(类别)p(样本)−−−−−（3.1−2）

p(类别∣∣样本) 表示样本属于类别的概率。贝叶斯分类器的思想是，将样本属于每个类别的概率 p(样本∣∣类别) 分别算出来，那个最大，样本就被分为哪个类别。
假设此时有三个类别，则可以算出三个值分别为 p(类别1∣∣样本)=0.2 ， p(类别2∣∣样本)=0.3 ， p(类别3∣∣样本)=0.5 ，由于 p(类别3|样本) 最大，所以样本就属于 类别3 .

重新研究式（5.1-2）发现对于同一个样本来说，比较 p(类别∣∣样本) 时可以不考虑 p(样本) ，因为对于同一个样本 p(样本) 是一样的，所以式（5.1-2）又可以简化为

p(类别∣∣样本)≅p(样本∣∣类别)p(类别)−−−−−（3.1−3）

式（5.1-3）是实际应用中所使用的分类准则，下面将叙述如何计算连续样本和离散样本时的贝叶斯分类器。

3.2 高斯贝叶斯分类器

3.2.1 理论简介

假设有训练样本集合

{xi,yi}，1≤i≤N，N为样本个数，xi∈Rn，yi∈[C1,C2,⋯,CK]

按照3.2节中的介绍要想对一个未知的样本进行分类需要计算式（3.1.3）

即计算 p(类别) 和 p(样本∣∣类别)

p()=p(Cj)=(yi=Cj)N−−−−−（3.1−4）

p(|)=p(x|y)=∏i=1np(xi|y)−−−−−（3.1−5）

p(xi|y) 采用高斯分布形式，如下

p(xi|y)=12πσ2y−−−−√exp⎡⎣⎢⎢−(xi−μy)22πσ2y⎤⎦⎥⎥−−−−−（3.1−5）

μy,σy 为类别 y 所对应的所有样本元素 xi 的均值和方差， y∈[C1,C2,⋯,CK] ，将 xi,yi 展开写成如下形式

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪X=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢x11x21x31x41⋮xN1x12x22x32x42⋮xN2⋯x1n⋯x2n⋯⋯⋱⋯x3nx4n⋮xNn⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥,Y=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢C1C1C3C1⋮C1⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎫⎭⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪−−−−−（3.1−6）

假设此时式（3.1-5）中的 y 此时取 C1 ， i 取为1，则此时将式（3.1-6）中X中的第一列中与 C1 所对应的项全部取出来，假设为 xC1=[xC11,xC12,xC13,⋯]

则此时

μy=mean(xC1)，σy=std(xC1)−−−−−（3.1−6）

其它元素的计算方法与之类似。

3.2.2 代码实现

第一步：生成训练样本和测试样本

def samples(n_samples, n_features = 10, classes = 5, rat = 0.2):
    见gaussian_nb.py

第二步：用训练数据训练模型

def train(self, x, y):
    见gaussian_nb.py

第三步：预测方法

def predict(self, x):
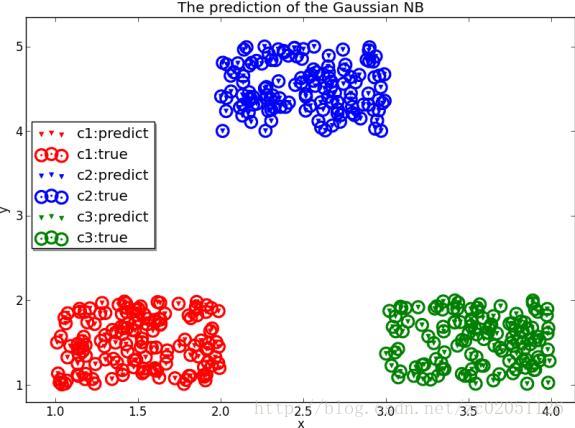
        见gaussian_nb.py

下图是朴素的高斯贝叶斯分类结果

图5.2.2.1 高斯贝叶斯分类结果

3.3 多项式贝叶斯分类器

多项式贝叶斯分类器主要用来处理特征是离散的情况，例如其很善于对文本进行分类，线面将以实际的例子介绍多项式贝叶斯分类器在文本分类中的应用。

3.3.1、构造数据集信息

假设存在如下五篇文档，并可以分成两大类good和bad

（1）’Nobody owns the water.’,’good’

（2）’the quick rabbit jumps fences’,’good’

（3）’the quick brown fox jumps’,’good’

（4）’buy pharmaceuticals now’,’bad’

（5）’make quick money at the online casino’,’bad’

需要统计的信息如下

a、构造词语-类别矩阵

从每篇文章中解析出所有不重复的词语，把这些词语在每个类别中出现的次数记录下来形成表1的词语-类别矩阵

表1 词语-类别矩阵

类别 词语	good	bad
Nobody	Num11(1)	Num12(0)
owns	Num21(1)	Num22(0)
quick	Num31(2)	Num32(1)
┆	┆	┆

表1表示在属于good类别的所有文章中，Nobody只出现在文章（1）中则Num11的值为1，在bad类别的所有文章中没有Nobody则Num12为0；而quick出现在文章（2）和（3）中所以Num31为2，同时quick出现在类别bad的文章（5）中一次，文章（4）中没有出现，所以Num32为1，其它的词语以此类推。

b、每种类别的个数

此处的文档共5篇，分为good和bad类，可以得到如表2的类别数统计信息

表2 类别信息

类别	数量
good	N1(3)
bad	N2(2)

3.3.2、计算特征（单词）概率

有了1中的信息就可以计算概率了，表示在给定B的条件下A的概率。我们需要求的是，例如要计算，则计算方法如下
p(quick|good)=Num31/N2=2/3=0.6666 ,quick出现在good中两次，而属于good的文章为3篇，所以最终的结果为2/3。

更一般的 p(词语∣∣类别)=词语出现在该类别中的总数/类别总数=表1中某个数/表2中某个数=Num(i,j)/N(j)

如果词语在表1中位于第i行，类别在表一中位于j列，则对应的类别在表2中位于j行，则

Num(i,j) 表示表1中i行j列对应的元素值， N(j) 表示表2中对应的j行元素值。

这种计算概率的方法，在计算初期，信息量较小时可能会出现个小的问题，如单词money只出现在文档（5）中，
并且这是一篇不好的文章，由于money只在一篇bad的文章中出现，而在任何good的文章中都没有出现，
所以最后计算money在good文章中出现的概率为0。显然这样做有些偏激，因为money完全可能是一个中性词，
只是其恰好出现在一篇bad的文章中而已。更合理的情况是随着单词越来越多地出现在一个分类文档中，
对应的概率也会趋近于某一个数值。为了解决这种缺点，引入加权平均方法，假设任意一个词语出现的概率为=0.5
（也可以根据先验知识设置该值），其还需要一个权重，此处设为=1（也可以根据先验知识设置该值），
同时为 p(词语∣∣类别) 也取一个权值 Wp=totals （某一词语出现在所有分类中的次数
（即，表1中某一行的元素相加，因为某一行对应于某一特征（词语）出现在good和bad类别中出现的次数）），
最终加权平均的概率表达为

p′(词语∣∣类别)=Pt∗wt+totals∗p(词语∣∣类别)wt+totals

3.3.3、计算整篇文档的频率

朴素的贝叶斯分类器假设每个特征（词语）的概率都是彼此独立的，所以计算某篇文档属于某一类别的概率，只需要将该篇文章中的所有不重复的特征属于某一类别的概率相乘，表达形式如下

p(文章|类别)=∐Ni=1p′(词语|类别)

其中 N 为某篇文章中所有特征（单词）的总数。

3.3.4、贝叶斯公式

我们真正需要的是，贝叶斯公式是一种对条件概率进行调换求解的方法，其通常写作

P(A|B)=P(B|A)∗P(A)P(B)

在此处，可写为

P(类别|文章)=P(文章|类别)∗P(类别)P(文章)

P(文章|类别) 在3中已经计算出来， P(类别) 为属于某一类别的
文章总数除以全部文章的数量，在用贝叶斯进行计算分类时，
需要把文章属于各个分类的概率都计算出来，然后比较，
对于各个分类 P(文章) 都是相同的所以不用计算 P(文章) ，所以最终的表达式为

P(类别|文章)≈P(文章|类别)∗P(类别)

**注意：由于贝叶斯分类器需要将概率连乘，如果词项过多将可能导致计算机计算时溢出，
所以可以将式 P(类别|文章)=P(文章|类别)∗P(类别) 两端取对数，如下

P′(类别|文章)∝log2(P(文章|类别)∗P(类别))

因为对数是单调增函数，所以经过对数变换
后就变成相加了，可以避免溢出。

3.3.5、选择分类

在实际的应用中，为了保准分类的准确性，
对于一篇将要被划分为某个分类的新文章而言，
其概率与其它所有分类的概率相比，必须大于某个指定的数值，
这个数值称为阈值，以垃圾邮件的分类为例，
如果要把一份邮件过滤到bad分类中，
设该邮件属于bad分类的概率为 Pbad ，属于good的概率为 Pgood ，只
有满足 Pbad>n∗Pgood 时才能把这封邮件划分到bad分类中，
否则就认为这封邮件是good分类。

3.3.6、费舍尔方法

1、针对词语的分类概率

贝叶斯方法，将 P(词语|类别) 的计算结果组合起来（连乘）的得
到了整篇文档的概率，然后再对其进行调换求解，
费舍尔方法将直接计算当一篇文档中出现某个特征时，
该文档属于某个分类的可能性，也就是计算 P(类别|词语) ，计算 P(类别|词语) 的方法如下

P(类别|词语)=词语属于某一分类的文档数出现词语的总文档数=Num(i,1)或Num(i,2)Num(i,1)+Num(i,2)

不过这种方法也会存在前文遇到的问题—算法接触到的词的次数太少，
所以可能会对概率估计的不准，因此要像前文那样进行加权平均

P′(类别|词语)=Pt∗wt+totals∗P(类别|词语)wt+totals

2、将各概率值组合起来

费舍尔方法的计算过程是将所有的概率相乘起来，然后取自然对数，然后再将结果乘以-2

P(类别|文档)=−2×ln(∐Ni=1P′(类别|词语i))

N为词语个数， ln 是自然对数。

3、对内容分类

与贝叶斯分类器相似，为了使分类结果准确，要为每个分类指定个下限，而后分类器会返回指定范围内的最大值，例如，在垃圾过滤器中可以将bad的阈值设置很高为0.6，将good分类的阈值设置的较低为0.2，这样做就可以将正常邮件被分到bad分类中的可能降到最低，同时也允许少量垃圾邮件进入到收件箱中，如果有的邮件good分类的分值低于0.2，good分类的分值低于0.6，都被划分到未知分类中。

3.3.7、增量式训练

在真实世界中所有的训练和分类都不可能一次性的完成，那么就需要将用户在训练期间所产生的与训练相关的数据保存起来，在下次训练的时候就不要重复训练了，这种支持分次训练的方式称之为增量式训练，在该算法中，每次训练时只要更新表1和表2的消息，并将之保存即可。

在分类时直接使用保存下来的表1和表2的消息就可以分类了。

4 总结

除了以上介绍的分类器外，还有神经网络、决策树、随机森林、Adaboost，支持向量机等，这里不做过多介绍。
分类算法属于有监督学习范畴，其需要先验的某些数据集对模型进行训练，用训练好的某些对未知数据进行分类，主要的流程如下：
1 将数据集（带标签的数据）按照一定的比例分成训练集和测试集，例如可以将80%的数据作为训练集，20%的数据作为测试集。
2 用训练集训练分类模型
3 用测试集测试模型的性能，如查看分类器的准确率召回率等评价指标，以确认模型的精度是否满足要求
4 用模型对未知类别的数据进行分类