Apollo无人驾驶课程笔记 第七课-控制
1. 控制简介
如何使用控制来运行轨迹呢?控制是驱使车辆前行的策略,对于汽车而言,最基本的控制输入为转向、加速、制动。
通常控制器使用一系列路径点来接收轨迹,控制器的任务是使用控制输入让车辆通过这些路径点。
首先控制器必须准确,意味着应避免偏离目标轨迹,这对于安全性来说也尤为重要,即使路面潮湿或者道路比较陡峭,控制器仍需要较为精确的执行轨迹:

其次控制策略对汽车具备可行性,例如,如果汽车正在向北行驶,而你希望汽车立即向东转,你可以在游戏中做到这一点,但在现实生活中却是不可能的任务:
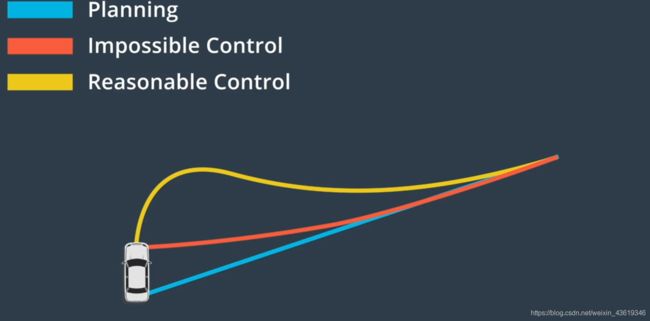
最后考虑的是平稳度(平顺性),舒适的驾驶非常重要,如果车辆行驶得不规律,会降低舒适感,那么乘客下次很可能就不会再乘坐它了。要使控制顺利进行,驱动必须是连续的,这意味着应避免突然转向、加速或制动:



总之目标是使用可行的控制输入,最大限度地降低与目标轨迹的偏差,最大限度地提高乘客的舒适度。
可用于实现这些目标的三种控制策略比例积分微分控制(PID)、线性二次调节器(LQR)、模型预测控制( MPC)。
2. Sebastian 介绍控制
什么是控制?控制就是指对方向盘、制动踏板、油门踏板的精细控制。控制是一门让汽车在既定轨迹上平稳运行的学问,首先从PID控制开始,PID控制是一个非常合适的控制机制,在这里了解基础知识,其次要了解的是线性二次调节器控制,最后是模型预测控制。
3. 控制流程_a
我们的控制器预计有两种输入:目标轨迹与车辆状态。
目标轨迹来自规划模块,再每个轨迹点处,规划模块指定一个位置和一个参考速度。在每个时间步都对轨迹进行更新:

我们还需要了解车辆状态,其中包括车辆位置,这通过本地化模块来计算,该状态还包括我们从车辆内部传感器获得的数据,如速度、转向和加速度。

我们使用这两个输入来计算目标轨迹与实际轨迹之间的偏差。
4. 控制流程_b
控制器的输出是控制输入(转向、加速、制动)的值,当偏离目标轨迹时,希望通过采取行动来纠正这种偏差。
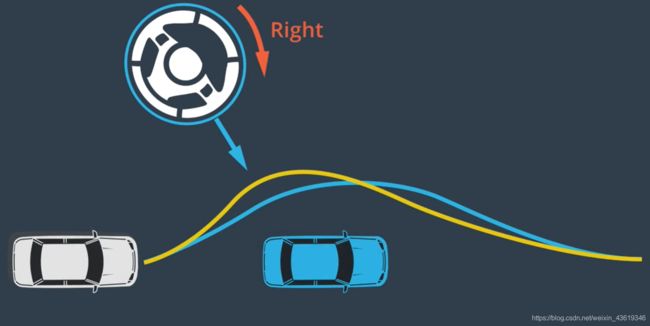
对于普通汽车,使用方向盘控制行驶方向(即转向),使用油门加速,使用刹车减速(即制动)。
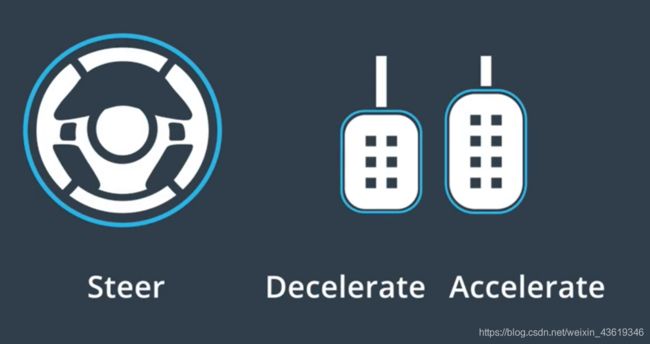
一旦将这三个值传递给车辆,汽车实际上已经开始无人驾驶了!
5. PID 控制_a
PID控制,这个控制器的优点在于它非常简单,只需知道与目标轨迹有多大的偏离。

PID 的为 P 代表“比例”(proportional),设想一辆车正试图遵循目标轨迹,P控制器在车辆开始偏离时,立即将其拉回目标轨迹。比例控制意味着车辆偏离越远,控制器就越难将其拉回目标轨迹。

6. PID 控制_b
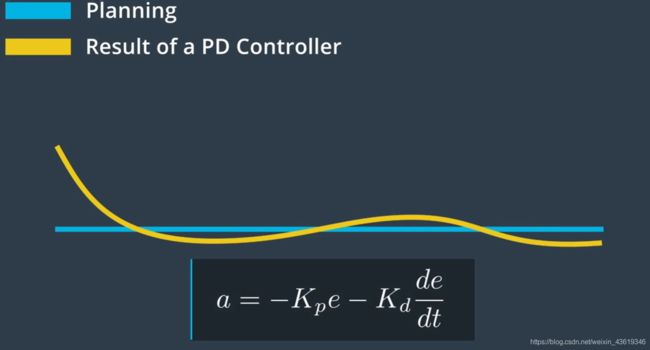
在实践中P控制器的一个问题在于很容易超出参考轨迹。
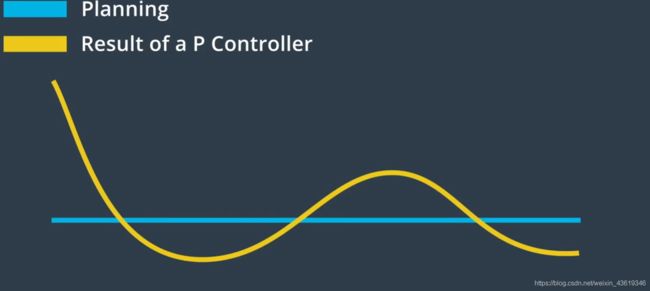
当车辆越来越接近目标轨迹时,需要控制器更加稳定。PID控制器中的D项致力于使运动处于稳定状态,D代表“微分”(derivative)。
PD控制器类似于 P 控制器,增加了一个阻尼项,可最大限度地减少控制器输出的变化速度。
7. PID 控制_c
PID 控制器中的最后一项 I 表示积分(Integral),该项负责纠正车辆的任何系统性偏差。例如转向可能失准,可能造成恒定的转向偏移。在这种情况下需要稍微向一侧转向以保持直行,为解决问题,控制器会对系统的累积误差进行惩罚。
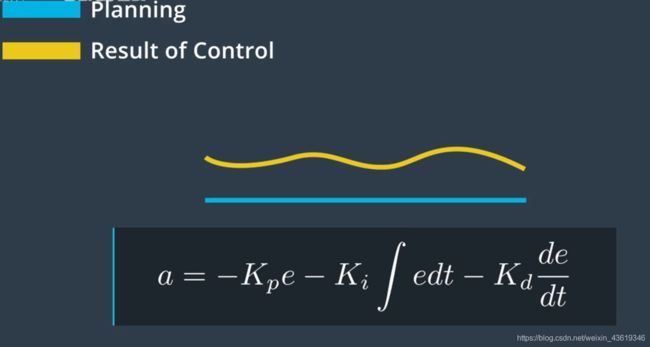
我们可以将 P , I , 和 D P,I,和D P,I,和D组件结合,构成PID控制器。
8. PID 优劣对比
对于 PID 控制器,只需知道你的车辆与目标轨迹之间的偏差。但是 PID 控制器只是一种线性算法,对于非常复杂的系统而言是不够的。例如为控制具有多个关节的四轴飞行器或机器人,需要建立机器人的物理模型,对无人驾驶车,需要应用不同的 PID 控制器来控制转向和加速,这意味着很难将横向和纵向控制结合起来。另一个问题是PID控制器依赖于实时误差测量,意味着受到测量延迟限制时可能会失效。
9. 线性二次调节器
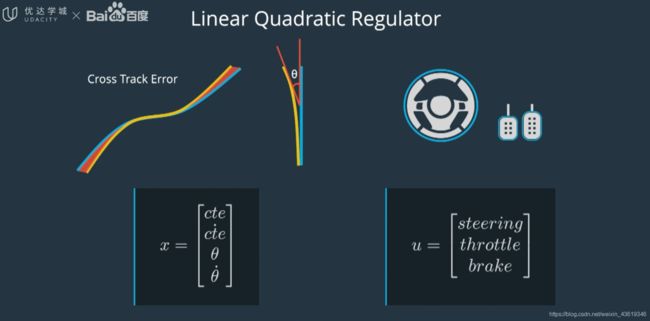
线性二次调节器(LQR)是基于模型的控制器,使用车辆的状态来使误差最小化。Apollo 使用 LQR 进行横向控制,横向控制包含四个组件:横向误差、横向误差的变化率、朝向误差、朝向的变化率。称这四个组件的集合为 x,这个集合 x 捕获车辆的状态。该车有三个控制输入:转向、加速、制动,将这个控制输入集合称为 u。
LQR处理线性控制,这种类型的模型可以用等式来表示: x ˙ = A x + B u \dot{x}=Ax+Bu x˙=Ax+Bu, x ˙ \dot{x} x˙向量是导数或 x x x向量的变化率,所以 x x x点的每个分量只是 x x x 相应分量的导数。等式 x ˙ = A x + B u \dot{x}=Ax+Bu x˙=Ax+Bu,该等式捕捉状态里的变化,即 x x x 点 是如何受当前状态 x x x和控制输入 u u u 的影响的。
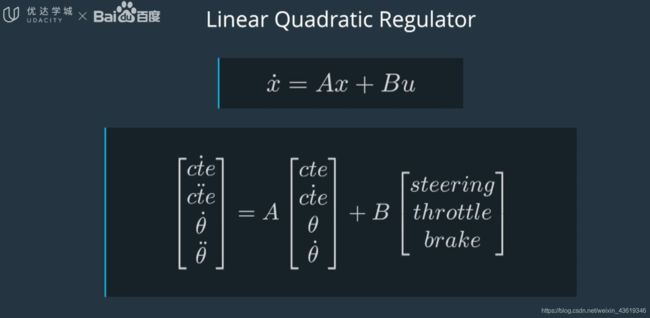
这个等式是线性的,因为用 Δ x \Delta x Δx 来改变 x x x 时,并用 Δ u \Delta u Δu 来改变 u u u , x ˙ \dot{x} x˙的变化 也会让这个等式成立。

理解了LQR 中的L,那么 Q 呢?这里的目标就像控制的目标一样典型,是为了让误差最小化,但也是希望尽可能少地使用控制输入,因为使用这些会有成本(比如耗费汽油或者电能)。为了尽量减少这些因素,可以保持误差的运行总和和控制输入的运行总和。
当汽车往右偏转得特别厉害之际,添加到误差总和中,当控制输入将汽车往左侧转时,从控制输入总和中减去一点。然而这种方法会导致问题,因为右侧的正误差只需将左侧的负误差消除即可,对控制输入来说也是如此。
相反可以让 x x x 乘以 u u u,这样负值也会产生正平方,称这些为二次项。
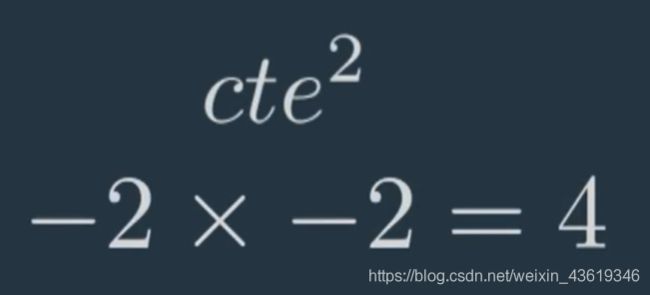
为这些项分配权重并将它们加在一起,最优的 u 应该加倍减总和,在数学中将这个值称为成本函数。
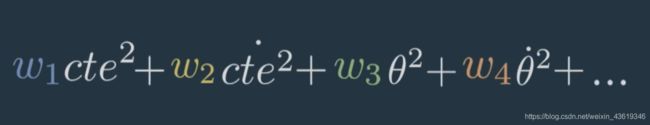
我们经常写出加权二次项的总和,以紧凑的矩阵形式呈现,这里 Q Q Q 和 R R R 代表 x x x 和 u u u 的权重集合, X T X^T XT 和 U T U^T UT 是转置矩阵,意味着它们几乎与 x x x 和 u u u 相同,只是重新排列以便矩阵乘法。 x x x 乘以 X T X^T XT, u u u 乘以 U T U^T UT,实质上是将每个矩阵乘以它自己。
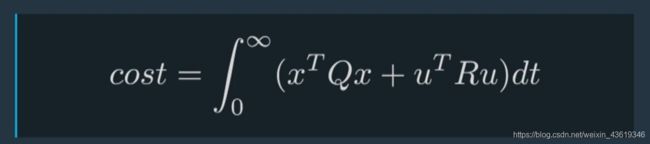
最小化成本函数是一个复杂的过程,但通常可以依靠数值计算器找到解决方案。Apollo就提供了一个这样的求解方案,再LQR中,控制方法被描述为 u = − K x u=-Kx u=−Kx,其中K代表一个复杂的skeme,代表如何从 x x x计算出 u u u,所以找到一个最优的 u u u就是找到一个最优的 K K K,许多工具都可以轻松的来求解 K K K,尤其是当你提供了模拟车辆物理的 A 、 B A、B A、B,以及 Q 、 R Q、R Q、R(它们是 x x x和 u u u的权重)。

10. 模型预测控制
模型预测控制(MPC)是一种更复杂的控制器,非常依赖于数学优化。但基本上可以将 MPC 归结为三个步骤:
- 建立车辆模型
- 使用优化引擎计算有限时间范围内的控制输入
- 然后执行第一组控制输入
MPC 是一个重复过程,计算一系列控制输入并优化该序列,但是控制器实际上只实现了序列中的第一组控制输入,然后控制器再次重复该循环。
为什么我们不执行整个控制输入序列呢?因为仅只采用了近似测量与计算,如果实现了整个控制输入序列,实际产生的车辆状态将与我们的模型有很大差异,最好在每个时间步不断地重新评估控制输入的最优序列。
11. 时间范围与车辆模型
MPC 的第一步为定义车辆模型,该模型近似于汽车的物理特性,特别估计了假如将一组控制输入应用于车辆时会发生什么。
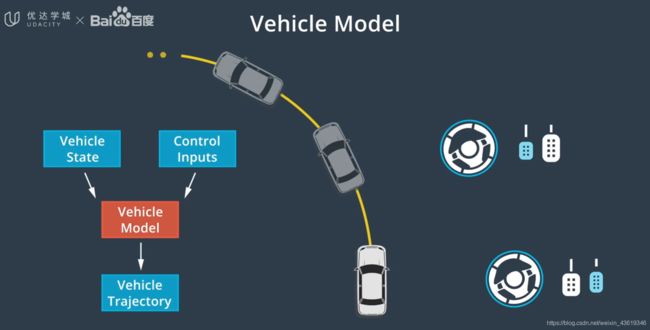
接下来决定 MPC 预测未来的能力,预测越深入,控制器就越精确,不过需要的时间也越长。所以需要在准确度与快速获取结果之间做出取舍,获取结果的速度越快,越能快速地将控制输入应用到实际车辆中。
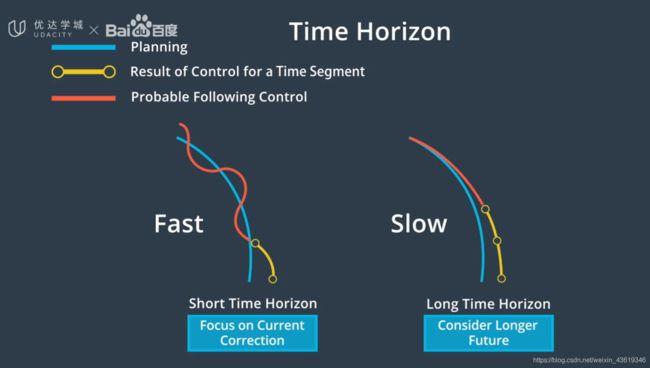
下一步是将模型发送到搜索最佳控制输入的优化引擎,该优化引擎的工作原理是通过搜索密集数学空间来寻求最佳解决方案,为缩小搜索范围优化引擎依赖于车辆模型的约束条件。
12. MPC 优化
优化引擎可间接评估控制输入是通过使用这些方法对车辆轨迹进行建模的,可根据成本函数对轨迹进行评估,成本函数主要基于与目标轨迹的偏差,其次基于其他因素如加速度和提升乘客舒适度的措施。
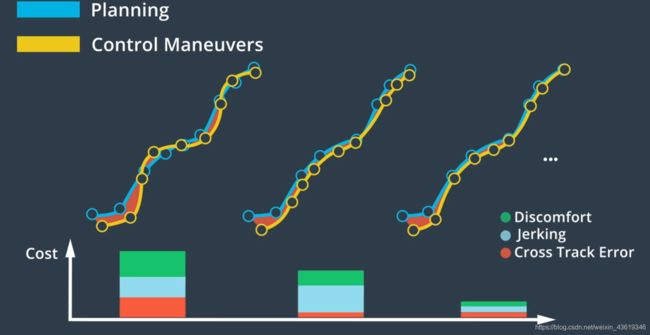
为使乘客感觉更舒适,对控制输入的调整应该很小,因为动作变化幅度过大会让乘客感到不舒服。根据具体情况,可能需要为其考虑进一步的成本并设计成本函数,模型、约束、成本函数合并在一起并作为优化问题加以解决。
13. MPC 优劣对比
模型预测控制考虑了车辆模型,因此比PID控制更精确,也适用于不同的成本函数。所以可以在不同情况下优化不同的成本,另一方面与PID控制相比,模型预测控制相对更复杂、更缓慢、更难以实现。在实践中无人驾驶车的控制可扩展性的重要程度,通常意味着值得为 MPC 投入实现成本,所以 MPC 成为了一个非常重要的无人驾驶车控制器。
也就是说MPC大有可为呀!
14. 项目示例:控制
15. 课程综述
在控制中,我们使用转向、加速和制动来运行我们的目标轨迹,我们研究了几种不同类型的控制器:PID控制是一种简单而强大的控制算法,二次线性调节器(LQR)和模型预测控制(MPC)是另外两种类型的控制器,它们更复杂,但也更强大、更准确。Apollo支持以上这所有的三种控制器,而你可以选择最适合自己的控制器!