你想要了解的贪心算法都在这里
贪心算法
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
基本思路
1.建立数学模型来描述问题;
2.把求解的问题分成若干个子问题;
3.对每一子问题求解,得到子问题的局部最优解;
4.把子问题的解局部最优解合成原来解问题的一个解。
算法实现
1.从问题的某个初始解出发。
2.采用循环语句,当可以向求解目标前进一步时,就根据局部最优策略,得到一个部分解,缩小问题的范围或规模。
3.将所有部分解综合起来,得到问题的最终解。
实例分析
实例1 背包问题
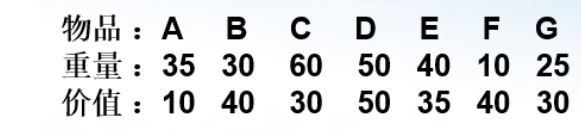
有一个背包,背包容量是M=150。有7个物品,物品可以分割成任意大小。要求尽可能让装入背包中的物品总价值最大,但不能超过总容量。
问题分析
1.目标函数: ∑pi最大,使得装入背包中的所有物品pi的价值加起来最大。
2.约束条件:装入的物品总重量不超过背包容量:∑wi<=M( M=150)
3.贪心策略:
选择价值最大的物品
选择价值最大的物品
选择单位重量价值最大的物品
有三个物品A,B,C,其重量分别为{30,10,20},价值分别为{60,30,80},背包的容量为50,分别应用三种贪心策略装入背包的物品和获得的价值如下图所示:

算法设计:
计算出每个物品单位重量的价值
按单位价值从大到小将物品排序
根据背包当前所剩容量选取物品
如果背包的容量大于当前物品的重量,那么就将当前物品装进去。否则,那么就将当前物品舍去,然后跳出循环结束。
#include运行结果
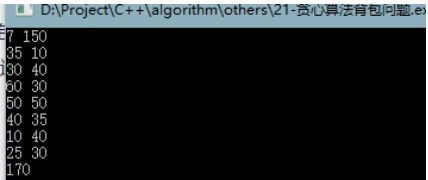
实例2 活动安排问题
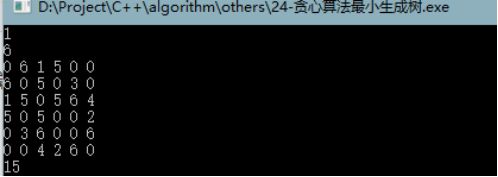
问题描述: 求一个连通无向图的最小生成树的代价(图边权值为正整数)。 输入 第一行是一个整数N(1<=N<=20),表示有多少个图需要计算。以下有N个图,第i图的第一行是一个整数M(1<=M<=50),表示图的顶点数,第i图的第2行至1+M行为一个M*M的二维矩阵,其元素ai,j表示图的i顶点和j顶点的连接情况,如果ai,j=0,表示i顶点和j顶点不相连;如果ai,j>0,表示i顶点和j顶点的连接权值。 输出 每个用例,用一行输出对应图的最小生成树的代价。 样例输入 1 样例输出 15 Kruskal算法简述 运行结果 在一个狭窄的走廊里将桌子从一个房间移动到另一个房间,走廊的宽度只能允许一个桌子通过。给出t,表示有t组测试数据。再给出n,表示要移动n个桌子。n下面有n行,每行两个数字,表示将桌子从a房间移到b房间。走廊的分布图如一图所示,每移动一个桌子到达目的地房间需要花10分钟,问移动n个桌子所需要的时间。 输入 3 输出 10 解题思路 我们首先输入每次移动的出发和结束房间,然后按每次移动的出发房间从小到大排序,然后直至所有的房间移动完毕。(代码1的解释) 代码3
设有n个活动的集合E={1,2,…,n},其中每个活动都要求使用同一资源,如演讲会场等,而在同一时间内只有一个活动能使用这一资源。每个活动i都有一个要求使用该资源的起始时间si和一个结束时间fi,且si 
(ps:活动结束时间按从小到大排序)
问题分析:
活动安排问题要求安排一系列争用某一公共资源的活动。用贪心算法可提供一个简单、漂亮的方法,使尽可能多的活动能兼容的使用公共资源。设有n个活动的集合{0,1,2,…,n-1},其中每个活动都要求使用同一资源,如会场等,而在同一时间内只有一个活动能使用这一资源。每个活动i都有一个要求使用该资源的起始时间starti和一个结束时间endi,且starti
算法设计:
若被检查的活动i的开始时间starti小于最近选择的活动j的结束时间endj,则不选择活动i,否则选择活动i加入集合中。运用该算法解决活动安排问题的效率极高。当输入的活动已按结束时间的非减序排列,算法只需O(n)的时间安排n个活动,使最多的活动能相容地使用公共资源。如果所给出的活动未按非减序排列,可以用O(nlogn)的时间重排。
代码实现:
代码1#include#include
6
0 6 1 5 0 0
6 0 5 0 3 0
1 5 0 5 6 4
5 0 5 0 0 2
0 3 6 0 0 6
0 0 4 2 6 0
假设 WN=(V,{E}) 是一个含有 n 个顶点的连通网,则按照克鲁斯卡尔算法构造最小生成树的过程为:先构造一个只含 n 个顶点,而边集为空的子图,若将该子图中各个顶点看成是各棵树上的根结点,则它是一个含有 n 棵树的一个森林。之后,从网的边集 E 中选取一条权值最小的边,若该条边的两个顶点分属不同的树,则将其加入子图,也就是说,将这两个顶点分别所在的两棵树合成一棵树;反之,若该条边的两个顶点已落在同一棵树上,则不可取,而应该取下一条权值最小的边再试之。依次类推,直至森林中只有一棵树,也即子图中含有 n-1条边为止。

算法难点:
(1)边的选择要求从小到大选择,则开始显然要对边进行升序排序。
(2)选择的边是否需要,则从判断该边加入后是否构成环入手。
算法设计:
(1)对边升序排序
在此采用链式结构,通过插入排序完成。每一结点存放一条边的左右端点序号、权值及后继结点指针
(2)边的加入是否构成环
一开始假定各顶点分别为一组,其组号为端点序号。选择某边后,看其两个端点是否在同一组中,即所在组号是否相同,如果是,表示构成了环,则舍去。 如果两个端点所在的组不同,则表示可以加入,则将该边两端的组合并成同一组。
代码实现:#include
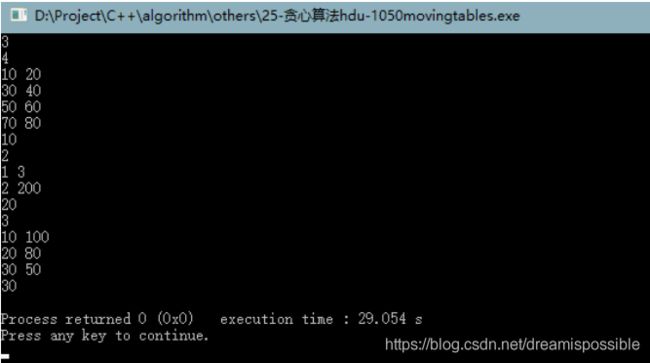
实例4 hdu1050-Moving Tables
题目描述
4
10 20
30 40
50 60
70 80
2
1 3
2 200
3
10 100
20 80
30 50
20
30
若移动多个桌子时,所需要经过的走廊没有重合处,即可以同时移动。若有一段走廊有m个桌子都要经过,一次只能经过一个桌子,则需要m*10的时间移动桌子。 设一个数组,下标值即为房间号。桌子经过房间时,该房间号为下标对应的数组值即加10。最后找到最大的数组值,即为移动完桌子需要的最短时间。(以上为代码2,代码3同这个思想)
注意:
1.可能出发位置比目的地房间大,无论大小,我们都可以看做从小的房间移动到大的房间
2.出发房间为偶数则减一,结束房间为奇数则加一

代码1(我自己感觉不是贪心算法,属于暴力破解吧,大家酌情考虑)#include#include#include