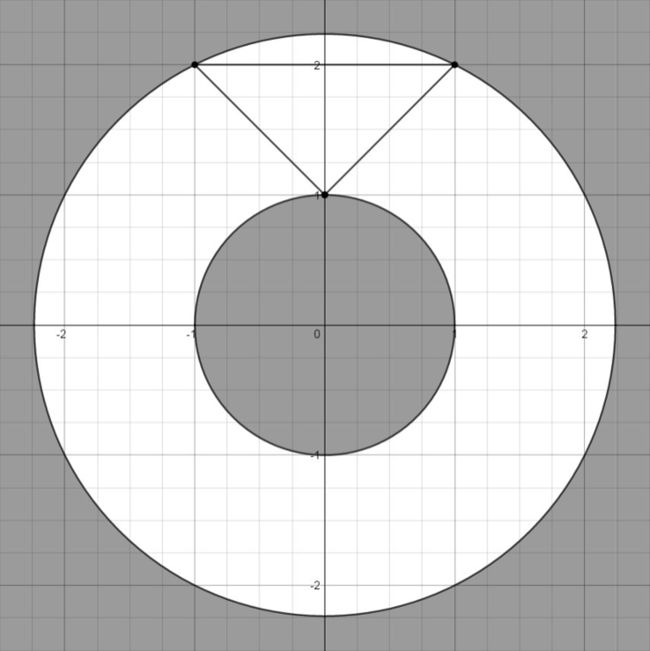
- Codeforces1637E Best Pair
特别萌新的小白
c++算法
tags枚举暴力中文题面给你一个长度为nnn的数组aaa。设cntxcnt_xcntx是数组中等于xxx的元素个数。再将f(x,y)f(x,y)f(x,y)定义为(cntx+cnty)⋅(x+y)(cnt_x+cnt_y)\cdot(x+y)(cntx+cnty)⋅(x+y)。此外,我们还得到了mmm个坏数对(xi,yi)(x_i,y_i)(xi,yi)。请注意,如果(x,y)(x,y)(x,y)
- Codeforces Round #771 (Div. 2)
狗蛋儿l
codeforcesleetcode
A.ReverseYouaregivenapermutationp1,p2,…,pnoflengthn.Youhavetochoosetwointegersl,r(1≤l≤r≤n)andreversethesubsegment[l,r]ofthepermutation.Thepermutationwillbecomep1,p2,…,pl−1,pr,pr−1,…,pl,pr+1,pr+2,…,pn.
- Codeforces Round 1004(Div.2) B. Two Large Bags 补题 + 题解 python
查理零世
python算法
B.TwoLargeBagshttps://codeforces.com/contest/2067/problem/B题目描述timelimitpertest:1secondmemorylimitpertest:256megabytesYouhavetwolargebagsofnumbers.Initially,thefirstbagcontainsnnnnumbers:a1,a2,…,ana_1
- Remove Exactly Two ( [Codeforces Round 1000 (Div. 2)](httpsmirror.codeforces.comcontest2063) )
BoBoo文睡不醒
acm训练集合搜索dfs数据结构
RemoveExactlyTwo(CodeforcesRound1000(Div.2))Recently,LittleJohngotatreefromhisaunttodecoratehishouse.Butasitseems,justonetreeisnotenoughtodecoratetheentirehouse.LittleJohnhasanidea.Maybehecanremoveafe
- Codeforces Round 977 (Div. 2)E1 Digital Village (Easy Version)(Floyd,贪心)
Auto114514
Codeforces算法c++数据结构图论
题目链接CodeforcesRound977(Div.2)E1DigitalVillage(EasyVersion)思路首先,我们注意到nnn的最大值只有400400400。因此,我们可以先用FloydFloydFloyd算法预处理出任意两座城市之间的最大延迟时间。之后,我们通过在线操作,每次贪心地选出最优的一个城市,并不断更新答案。即,我们先选出k=1k=1k=1时的最优解,之后从剩下的点里面挑
- poj 1142 Smith Numbers(数论:欧拉函数变形)
殷华
数学/数论
给定一个数n找出大于n的最小smith数smith数定义如下:一个数n为smith数当且仅当它的所有质因子各位数之和等于n的所有位数之和且n不是素数那么给定一个n,我们就可以每次+1判断是否为smith数这道题唯一的难点就在于找到一个数的所有素数因子套用欧拉函数变形即可375ms代码如下:#include#include#defineLLlonglongLLn;intget_ans(LLn){in
- CF Round 1004 记录 & 题解(div.1 A - D1 & div.2 D - F)
JeremyHe1209
算法
今天上午VPCodeforcesRound1004(Div.2),下午改CodeforcesRound1004(Div.1)。上午C题因为少判了一个条件,罚时吃饱了。[Codeforces2066A&2067D]ObjectIdentification神奇交互题。观察到一个性质:对象AAA的答案可能是000,但对象BBB的答案不可能是000。若x1,x2,…,xnx_1,x_2,\dots,x_n
- 探索约数:试除法,约数之和,最大公约数
Lostgreen
数据结构&算法算法最大公约数
引言约数(Divisor)是数论中的基本概念之一,指能够整除某个数的整数。约数在数学、计算机科学和密码学中有着广泛的应用。本文将详细介绍约数的相关知识,包括试除法求约数、最大公约数算法(如辗转相除法和更相减损术),并阐明这些算法的原理和步骤。1.试除法求约数1.1算法原理试除法是一种简单直观的求约数的方法。对于一个数nnn,如果ddd是nnn的约数,则nnn能被ddd整除。通过遍历1到n\sqrt
- ACM培训4
ZIZIZIZIZ()
算法笔记
学习总结--基础数论大多为模板一、GCD(最大公约数)①辗转相除法longlonggcd(longa,longb){longlongr;while(b!=0){r=a%b;a=b;b=r;}returna;}②扩展欧几里得算法intexgcd(inta,intb,int&x,int&y){if(b==0){x=1;y=0;returnaa;}intans=exgcd(b,a%b,x,y);intk
- 【数论】—— 素数
Tom_wsc
数论算法
素数定义因数只有111和这个数本身的数被称作素数。注意:111既不是素数也不是合数,222是最小的素数。两个关于素数的定理唯一分解定理对于任意大于111的整数xxx,都可以分解成若干个素数的乘积:x=p1a1×p2a2×p3a3×⋯×pnan(ai∈Z+)x=p_1^{a_1}\timesp_2^{a_2}\timesp_3^{a_3}\times\cdots\timesp_n^{a_n}(a_i
- 【运行别超时】最近小何去在我们学校的比赛中遇到一个有意思的题,答案做出来了,但运行总是超时。这怎么解决呢?来看看吧。
小浩~
c语言
题目内容如下:小C最近在研究数论,他发现质数有太多美妙的性质了,于是他想要统计一下一段区域里的数有多少是质数,请你编程帮他解决这个问题吧。输入格式:第一行一个正整数t,表示数据组数。(1≤t≤105)接下来t行,每行两个正整数l,r,表示区间的左右端点。(1≤l≤r≤106)输出格式:每组数据输出一个整数,表示闭区间[l,r]中的质数数量输入样例:21326输出样例:在这里给出相应的输出。例如:2
- 2025年日祭
JeremyHe1209
笔记
本文将同步发表于洛谷(暂无法访问)、CSDN与Github个人博客(暂未发布)本蒟自2025.2.8开始半停课。任务计划(站外题与专题)数了一下,通过人数比较高的题,也就是我准备补的题,刚好差不多100道题。于是……摆烂百题计划开始!(糖丸了)(2025.2.8)NetworkNetworkofSchoolsDP优化——矩阵数论——容斥、二项式反演DP优化——斜率优化数据结构——左偏树数据结构——
- SMU winter 2025 Personal Round 2
osir.
枚举
Problem-D-Codeforces思路://在给定数中取x,y,z使得(x-y)^2+(y-z)^2+(z-x)^2最值.//容易发现是找最接近的三个数字,但是怎么找呢//经验总结(没想到是枚举中间那个),其中一个数字是枚举的(总是枚举中间那个,对于这个题中间那个就是中间大那个).剩下两个数字呢?--可以二分//假设xusingnamespacestd;#defineintlonglong#
- 解析数论基础:第三十三章 零点分布(二)
AI天才研究院
计算AI大模型企业级应用开发实战DeepSeekR1&大数据AI人工智能大模型计算科学神经计算深度学习神经网络大数据人工智能大型语言模型AIAGILLMJavaPython架构设计AgentRPA
解析数论基础:第三十三章零点分布(二)作者:禅与计算机程序设计艺术/ZenandtheArtofComputerProgramming关键词:解析数论、黎曼ζ函数、零点分布、素数定理、蒙哥马利猜想、配对相关函数、随机矩阵理论1.背景介绍1.1问题的由来解析数论是现代数学的重要分支,它利用复变函数论等分析学的方法研究数论问题。其中一个核心课题就是研究黎曼ζ函数的性质,特别是它的零点分布。这个问题不仅
- 【密码学基础】RSA加密算法
Mr.zwX
隐私计算及密码学基础密码学安全
1RSA介绍RSA是一种非对称加密算法,即加密和解密时用到的密钥不同。加密密钥是公钥,可以公开;解密密钥是私钥,必须保密保存。基于一个简单的数论事实:两个大质数相乘很容易,但想要对其乘积进行因式分解却极其困难,因此可以将乘积公开作为加密密钥,即公钥;而两个大质数组合成私钥。2密钥对的生成step1生成N(公钥和私钥的一部分)首先选取两个互为质数的数ppp和qqq(p≠q,gcd(p,q)=1p\n
- Codeforces Educational Codeforces Round 170 (Rated for Div. 2)
关于SPFA它死了
Codeforces算法c++
A-TwoScreens大意:给两个字符串,每次在两个空子符串进行两种操作1、字符串末尾加一个任意字母2、一个字符串全部复制给另一个字符串求得到给定的两个字符串的最小操作数思路:看最前面有多少相等即可当时想多了。。。代码:#includeusingnamespacestd;#defineintlonglongconstintN=2e5+10,INF=0x3f3f3f3f;constintmod=1
- [CodeForces]8
天之道,利而不害
codeforce
G.MaximizetheRemainingString由小写字母组成的字符串sss,每次从中选取重复的字母进行删除,直到该字符串中的每个字母都只出现一次。问:最终形成的字典序最大的字符串,比如ababababababababab,答案为bababa。1≤len(s)≤2000001\leqlen(s)\leq2000001≤len(s)≤200000题解记s=a1a2a3⋯ans=a_1a_2a
- C - Nastya Is Transposing Matrices CodeForces - 1136C
Gee_Zer
思维
C.NastyaIsTransposingMatricestimelimitpertest1secondmemorylimitpertest256megabytesinputstandardinputoutputstandardoutputNastyacametoherinformaticslesson,andherteacherwhois,bytheway,alittlebitfamousher
- An impassioned circulation of affection ( Codeforces Round 418 (Div. 2) )
BoBoo文睡不醒
acm训练集合暴力枚举dp双指针
Animpassionedcirculationofaffection(CodeforcesRound418(Div.2))Nadeko’sbirthdayisapproaching!Asshedecoratedtheroomfortheparty,alonggarlandofDianthus-shapedpaperpieceswasplacedonaprominentpartofthewall.
- Codeforces Round 988 (Div. 3)
BoBoo文睡不醒
codeforces笔记
CodeforcesRound988(Div.3)C.Superultra’sFavoritePermutationtimelimitpertest2secondsmemorylimitpertest256megabytesSuperultra,alittleredpanda,desperatelywantsprimogems.Inhisdreams,avoicetellshimthathe
- Nastya Is Transposing Matrices ( Codeforces Round 546 (Div. 2) )
BoBoo文睡不醒
acm训练集合构造
NastyaIsTransposingMatrices(CodeforcesRound546(Div.2))Nastyacametoherinformaticslesson,andherteacherwhois,bytheway,alittlebitfamousheregaveherthefollowingtask.TwomatricesAAAandBBBaregiven,eachofthemha
- Not Escaping ( Codeforces Round 766 (Div. 2) )
BoBoo文睡不醒
acm训练集合dp数据结构模拟最短路
NotEscaping(CodeforcesRound766(Div.2))MajorRamisbeingchasedbyhisarchenemyRaghav.Rammustreachthetopofthebuildingtoescapeviahelicopter.Thebuilding,however,isonfire.Rammustchoosetheoptimalpathtoreachthet
- 【codeforces 764B】Timofey and cubes
adgnfega11455
数据结构与算法
timelimitpertest1secondmemorylimitpertest256megabytesinputstandardinputoutputstandardoutputYoungTimofeyhasabirthdaytoday!Hegotkitofncubesasabirthdaypresentfromhisparents.Everycubehasanumberai,whichisw
- Codeforces Round 130 (Div. 2) E. Blood Cousins(LCA+DFS序+二分)【2100】
Auto114514
ACM—树深度优先算法图论
题目链接https://codeforces.com/contest/208/problem/E思路此题有两个要点:第一,快速找到节点uuu的ppp级祖先。第二,在以节点uuu为根的子树中找到与节点uuu深度相同的节点的个数。对于第一点,我们可以使用LCA算法在树上倍增,实现快速查询。对于第二点,我们可以按照深度,将所有节点的DFS序全部存储到vector中,因为DFS序的单调性,直接二分查找即可
- Codeforces Round 276 (Div. 1) B. Maximum Value(数学+二分)【2100】
Auto114514
ACM—数学算法
题目链接https://codeforces.com/contest/484/problem/B思路a mod ba\,mod\,bamodb可以转化成a−k×ba-k\timesba−k×b,其中k=⌊ab⌋k=\left\lfloor\frac{a}{b}\right\rfloork=⌊ba⌋。我们发现k×busingnamespacestd;#defineintlonglong#define
- Codeforces Round 642 (Div. 3) E. K-periodic Garland(DP+前缀和)
Auto114514
ACM—DP动态规划算法
题目链接https://codeforces.com/contest/1353/problem/E思路令dp[i][0/1]dp[i][0/1]dp[i][0/1]分别表示第iii个字符是000或者111时的前iii个字符组成的花环所需的最少操作次数。如果第iii个字符变为111,分为两种情况:第一种情况是第i−ki-ki−k个字符必须为111,且[i−k+1,i−1][i-k+1,i-1][i−
- Codeforces Round 974 (Div. 3) H题 Robin Hood Archery(基础莫队,随机异或哈希)
Auto114514
Codeforces哈希算法散列表算法c++数据结构
题目链接CodeforcesRound974(Div.3)H题RobinHoodArchery思路1因为警长是后手,按照最优的策略,只有每一种数的个数是偶数个的时候,警长会平局,否则警长会输。随着询问区间端点的变化,答案的转移是O(1)O(1)O(1)的。因此,我们可以使用基础莫队进行离线求解。代码1#pragmaGCCoptimize("O2")#pragmaGCCoptimize("O3")#
- F. Greetings
L_M_TY
算法归并排序求逆序对
题目链接:Problem-F-Codeforces题目大意:给你n个线段,求有多少对(两个)线段满足完全覆盖,例如:设一个线段有a,b两点,满足aiusingnamespacestd;usingi64=longlong;usingi128=__int128;//求逆序对i64msort(vector&a,vector&b,intL,intR){if(L==R)return0;i64res=0;in
- Epidemic in Monstropolis( Codeforces Round 378 (Div. 2) )
BoBoo文睡不醒
acm训练集合模拟双指针贪心
EpidemicinMonstropolis(CodeforcesRound378(Div.2))TherewasanepidemicinMonstropolisandallmonstersbecamesick.Torecover,allmonsterslinedupinqueueforanappointmenttotheonlydoctorinthecity.Soon,monstersbecam
- F. Ira and Flamenco
L_M_TY
算法滑动窗口乘法原理乘法逆元
题目链接:Problem-F-Codeforces题目大意:给n,mn个数让从中选m个数满足一下条件:1.m个数互不相同2.里面的任意两个数相减的绝对值不能超过m求这n个数有多少组数据满足。第一行包含一个整数t(1≤t≤1e4)-测试用例数。每个测试用例的第一行包含整数n和m(1≤m≤n≤2⋅1e5)每个测试用例的第二行包含n个整数a1,a2,…,an(1≤ai≤1e9)。保证所有测试用例的n之和
- HttpClient 4.3与4.3版本以下版本比较
spjich
javahttpclient
网上利用java发送http请求的代码很多,一搜一大把,有的利用的是java.net.*下的HttpURLConnection,有的用httpclient,而且发送的代码也分门别类。今天我们主要来说的是利用httpclient发送请求。
httpclient又可分为
httpclient3.x
httpclient4.x到httpclient4.3以下
httpclient4.3
- Essential Studio Enterprise Edition 2015 v1新功能体验
Axiba
.net
概述:Essential Studio已全线升级至2015 v1版本了!新版本为JavaScript和ASP.NET MVC添加了新的文件资源管理器控件,还有其他一些控件功能升级,精彩不容错过,让我们一起来看看吧!
syncfusion公司是世界领先的Windows开发组件提供商,该公司正式对外发布Essential Studio Enterprise Edition 2015 v1版本。新版本
- [宇宙与天文]微波背景辐射值与地球温度
comsci
背景
宇宙这个庞大,无边无际的空间是否存在某种确定的,变化的温度呢?
如果宇宙微波背景辐射值是表示宇宙空间温度的参数之一,那么测量这些数值,并观测周围的恒星能量输出值,我们是否获得地球的长期气候变化的情况呢?
&nbs
- lvs-server
男人50
server
#!/bin/bash
#
# LVS script for VS/DR
#
#./etc/rc.d/init.d/functions
#
VIP=10.10.6.252
RIP1=10.10.6.101
RIP2=10.10.6.13
PORT=80
case $1 in
start)
/sbin/ifconfig eth2:0 $VIP broadca
- java的WebCollector爬虫框架
oloz
爬虫
WebCollector主页:
https://github.com/CrawlScript/WebCollector
下载:webcollector-版本号-bin.zip将解压后文件夹中的所有jar包添加到工程既可。
接下来看demo
package org.spider.myspider;
import cn.edu.hfut.dmic.webcollector.cra
- jQuery append 与 after 的区别
小猪猪08
1、after函数
定义和用法:
after() 方法在被选元素后插入指定的内容。
语法:
$(selector).after(content)
实例:
<html>
<head>
<script type="text/javascript" src="/jquery/jquery.js"></scr
- mysql知识充电
香水浓
mysql
索引
索引是在存储引擎中实现的,因此每种存储引擎的索引都不一定完全相同,并且每种存储引擎也不一定支持所有索引类型。
根据存储引擎定义每个表的最大索引数和最大索引长度。所有存储引擎支持每个表至少16个索引,总索引长度至少为256字节。
大多数存储引擎有更高的限制。MYSQL中索引的存储类型有两种:BTREE和HASH,具体和表的存储引擎相关;
MYISAM和InnoDB存储引擎
- 我的架构经验系列文章索引
agevs
架构
下面是一些个人架构上的总结,本来想只在公司内部进行共享的,因此内容写的口语化一点,也没什么图示,所有内容没有查任何资料是脑子里面的东西吐出来的因此可能会不准确不全,希望抛砖引玉,大家互相讨论。
要注意,我这些文章是一个总体的架构经验不针对具体的语言和平台,因此也不一定是适用所有的语言和平台的。
(内容是前几天写的,现附上索引)
前端架构 http://www.
- Android so lib库远程http下载和动态注册
aijuans
andorid
一、背景
在开发Android应用程序的实现,有时候需要引入第三方so lib库,但第三方so库比较大,例如开源第三方播放组件ffmpeg库, 如果直接打包的apk包里面, 整个应用程序会大很多.经过查阅资料和实验,发现通过远程下载so文件,然后再动态注册so文件时可行的。主要需要解决下载so文件存放位置以及文件读写权限问题。
二、主要
- linux中svn配置出错 conf/svnserve.conf:12: Option expected 解决方法
baalwolf
option
在客户端访问subversion版本库时出现这个错误:
svnserve.conf:12: Option expected
为什么会出现这个错误呢,就是因为subversion读取配置文件svnserve.conf时,无法识别有前置空格的配置文件,如### This file controls the configuration of the svnserve daemon, if you##
- MongoDB的连接池和连接管理
BigCat2013
mongodb
在关系型数据库中,我们总是需要关闭使用的数据库连接,不然大量的创建连接会导致资源的浪费甚至于数据库宕机。这篇文章主要想解释一下mongoDB的连接池以及连接管理机制,如果正对此有疑惑的朋友可以看一下。
通常我们习惯于new 一个connection并且通常在finally语句中调用connection的close()方法将其关闭。正巧,mongoDB中当我们new一个Mongo的时候,会发现它也
- AngularJS使用Socket.IO
bijian1013
JavaScriptAngularJSSocket.IO
目前,web应用普遍被要求是实时web应用,即服务端的数据更新之后,应用能立即更新。以前使用的技术(例如polling)存在一些局限性,而且有时我们需要在客户端打开一个socket,然后进行通信。
Socket.IO(http://socket.io/)是一个非常优秀的库,它可以帮你实
- [Maven学习笔记四]Maven依赖特性
bit1129
maven
三个模块
为了说明问题,以用户登陆小web应用为例。通常一个web应用分为三个模块,模型和数据持久化层user-core, 业务逻辑层user-service以及web展现层user-web,
user-service依赖于user-core
user-web依赖于user-core和user-service
依赖作用范围
Maven的dependency定义
- 【Akka一】Akka入门
bit1129
akka
什么是Akka
Message-Driven Runtime is the Foundation to Reactive Applications
In Akka, your business logic is driven through message-based communication patterns that are independent of physical locatio
- zabbix_api之perl语言写法
ronin47
zabbix_api之perl
zabbix_api网上比较多的写法是python或curl。上次我用java--http://bossr.iteye.com/blog/2195679,这次用perl。for example: #!/usr/bin/perl
use 5.010 ;
use strict ;
use warnings ;
use JSON :: RPC :: Client ;
use
- 比优衣库跟牛掰的视频流出了,兄弟连Linux运维工程师课堂实录,更加刺激,更加实在!
brotherlamp
linux运维工程师linux运维工程师教程linux运维工程师视频linux运维工程师资料linux运维工程师自学
比优衣库跟牛掰的视频流出了,兄弟连Linux运维工程师课堂实录,更加刺激,更加实在!
-----------------------------------------------------
兄弟连Linux运维工程师课堂实录-计算机基础-1-课程体系介绍1
链接:http://pan.baidu.com/s/1i3GQtGL 密码:bl65
兄弟连Lin
- bitmap求哈密顿距离-给定N(1<=N<=100000)个五维的点A(x1,x2,x3,x4,x5),求两个点X(x1,x2,x3,x4,x5)和Y(
bylijinnan
java
import java.util.Random;
/**
* 题目:
* 给定N(1<=N<=100000)个五维的点A(x1,x2,x3,x4,x5),求两个点X(x1,x2,x3,x4,x5)和Y(y1,y2,y3,y4,y5),
* 使得他们的哈密顿距离(d=|x1-y1| + |x2-y2| + |x3-y3| + |x4-y4| + |x5-y5|)最大
- map的三种遍历方法
chicony
map
package com.test;
import java.util.Collection;
import java.util.HashMap;
import java.util.Iterator;
import java.util.Map;
import java.util.Set;
public class TestMap {
public static v
- Linux安装mysql的一些坑
chenchao051
linux
1、mysql不建议在root用户下运行
2、出现服务启动不了,111错误,注意要用chown来赋予权限, 我在root用户下装的mysql,我就把usr/share/mysql/mysql.server复制到/etc/init.d/mysqld, (同时把my-huge.cnf复制/etc/my.cnf)
chown -R cc /etc/init.d/mysql
- Sublime Text 3 配置
daizj
配置Sublime Text
Sublime Text 3 配置解释(默认){// 设置主题文件“color_scheme”: “Packages/Color Scheme – Default/Monokai.tmTheme”,// 设置字体和大小“font_face”: “Consolas”,“font_size”: 12,// 字体选项:no_bold不显示粗体字,no_italic不显示斜体字,no_antialias和
- MySQL server has gone away 问题的解决方法
dcj3sjt126com
SQL Server
MySQL server has gone away 问题解决方法,需要的朋友可以参考下。
应用程序(比如PHP)长时间的执行批量的MYSQL语句。执行一个SQL,但SQL语句过大或者语句中含有BLOB或者longblob字段。比如,图片数据的处理。都容易引起MySQL server has gone away。 今天遇到类似的情景,MySQL只是冷冷的说:MySQL server h
- javascript/dom:固定居中效果
dcj3sjt126com
JavaScript
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml&
- 使用 Spring 2.5 注释驱动的 IoC 功能
e200702084
springbean配置管理IOCOffice
使用 Spring 2.5 注释驱动的 IoC 功能
developerWorks
文档选项
将打印机的版面设置成横向打印模式
打印本页
将此页作为电子邮件发送
将此页作为电子邮件发送
级别: 初级
陈 雄华 (
[email protected]), 技术总监, 宝宝淘网络科技有限公司
2008 年 2 月 28 日
&nb
- MongoDB常用操作命令
geeksun
mongodb
1. 基本操作
db.AddUser(username,password) 添加用户
db.auth(usrename,password) 设置数据库连接验证
db.cloneDataBase(fromhost)
- php写守护进程(Daemon)
hongtoushizi
PHP
转载自: http://blog.csdn.net/tengzhaorong/article/details/9764655
守护进程(Daemon)是运行在后台的一种特殊进程。它独立于控制终端并且周期性地执行某种任务或等待处理某些发生的事件。守护进程是一种很有用的进程。php也可以实现守护进程的功能。
1、基本概念
&nbs
- spring整合mybatis,关于注入Dao对象出错问题
jonsvien
DAOspringbeanmybatisprototype
今天在公司测试功能时发现一问题:
先进行代码说明:
1,controller配置了Scope="prototype"(表明每一次请求都是原子型)
@resource/@autowired service对象都可以(两种注解都可以)。
2,service 配置了Scope="prototype"(表明每一次请求都是原子型)
- 对象关系行为模式之标识映射
home198979
PHP架构企业应用对象关系标识映射
HELLO!架构
一、概念
identity Map:通过在映射中保存每个已经加载的对象,确保每个对象只加载一次,当要访问对象的时候,通过映射来查找它们。其实在数据源架构模式之数据映射器代码中有提及到标识映射,Mapper类的getFromMap方法就是实现标识映射的实现。
二、为什么要使用标识映射?
在数据源架构模式之数据映射器中
//c
- Linux下hosts文件详解
pda158
linux
1、主机名: 无论在局域网还是INTERNET上,每台主机都有一个IP地址,是为了区分此台主机和彼台主机,也就是说IP地址就是主机的门牌号。 公网:IP地址不方便记忆,所以又有了域名。域名只是在公网(INtERNET)中存在,每个域名都对应一个IP地址,但一个IP地址可有对应多个域名。 局域网:每台机器都有一个主机名,用于主机与主机之间的便于区分,就可以为每台机器设置主机
- nginx配置文件粗解
spjich
javanginx
#运行用户#user nobody;#启动进程,通常设置成和cpu的数量相等worker_processes 2;#全局错误日志及PID文件#error_log logs/error.log;#error_log logs/error.log notice;#error_log logs/error.log inf
- 数学函数
w54653520
java
public
class
S {
// 传入两个整数,进行比较,返回两个数中的最大值的方法。
public
int
get(
int
num1,
int
nu
![]() ), and coordinates of point P.
), and coordinates of point P.![]() .
.