erygreat

吴恩达神经网络第一课学习笔记

0.前言

什么是神经网络？
神经网络是上个世纪出现的产物，其思想就是模拟人体神经网络的方式来实现机器的自主学习。他在许多领域都会有使用，例如：语音识别、图像识别、语言翻译等。

神经网络的思想如下图所示：

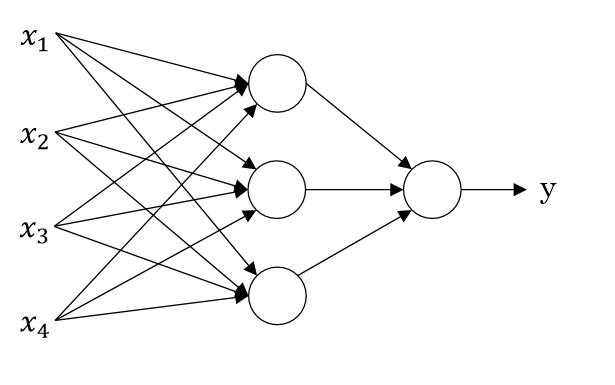
假设 x1 表示房价； x2 表示房子大小； x3 买房者所拥有的资金； x4 表示房子所在地区的空气质量等等，当然实际生活中还可能会考虑许多东西，这里就不举例了。而 y 表示对于房子的是否想买的态度，即想买或不想买。那么神经网络的工作就是将一个房子的上面四个变量放入进去，而神经网络给你预测出你是否想买。

那么他是怎么预测的呢？我们知道房价和房子大小往往是存在正相关性的，即房子越大房价越高，在这里我们将它们统称为“房子的状况”；“买房者所拥有的资金”以及一些其他的买房者的信息统称为“买房者的状况”；“房子周边的空气质量”有决定这“房子周边环境”。因此第二层的三个圆圈，可以看做：“房子的状况”、“买房者的状况”、“房子周边环境”。而第三层的一个圆圈可以看做“对房子的评分”。然后如果评分大于一个值，那么表示买，如果小于表示不买。

神经网络就是做了那么一个事情，我们经过一定的计算可以根据前面的节点，来获取下一个节点表示的特征，来达到预测的目的。那么问题来了，在上面图中第二层的三个圆各代表哪一个情况呢？答案是无法预知，有可能上面三种情况，有可能是上面情况中的两种，有可能是一些其他的有相关性的情况，甚至可能是一些我们经验无法解释的组合。正因为这样，所以神经网络被诟病为“黑盒”，里面的东西往往无法预测也无法解释。

我们先从一个节点来解释，神经网络的工作方式。

附：在本文中，激活函数使用sigmoid函数,数据集使用鸢尾花数据集前100行,可以在R中直接输”iris”出现，在python中

from  sklearn  import datasets
iris = datasets.load_iris()

并将前50行数据的Species设置为0，后50行的设置为1

1. 神经元

神经网络是由一个个神经元构成的，例如在上面的例子中，第一层有三个神经元，第二层有一个神经元。这里我们先讲一讲什么是神经元，神经元如下图所示

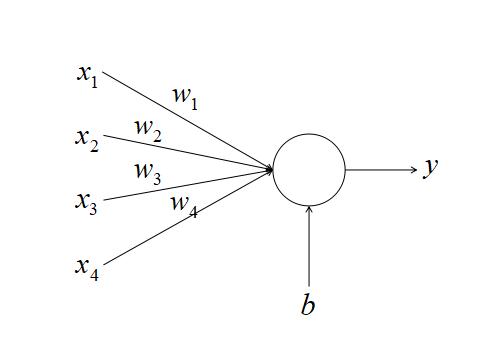
在神经元中，会对 x 先进行加权求和，在将加权求和的结果进行线性变换以得到 y 。在上面中 x 为传入参数， w 为权重， b 为截距， y 为输出结果。

举个例子，假设

今天气温为20度，风力2级，湿度15%，空气质量51；
明天气温为25度，风力1级，湿度10%，空气质量152；
后天气温为22度，风力5级，湿度12%，空气质量51。

对于是否适合运动来说

气温的权重为10；
风力权重为-50；
湿度权重为-5；
空气质量权重为-3；
截距200。

那么加权求和的结果为：今天指数为72，明天指数为-156，后天指数为-33.我们再使用sigmoid函数 y=11+e−x 进行线性变换,可以近似得到”1、0、0”，因此可以得出今天适合运动，明天和后天不适合运动的结论。当然这个例子十分粗糙但是神经网络就是这样子预测的。

上面的公式为

z = \sum i = 0 n w i x i + b y = f (x) f (x) = σ (x) = 1 1 + e - x

其中 f 称为激活函数（activation function）。在本例子中采用sigmoid（ σ ）函数，这个概念后面会说。

上面的式子可能只会出现一次，在后面的使用中我们矩阵来代替多个样本，因此对于存在变量 (x1,x2,x3,...,xn) ,存在样本 (x(1),x(2),x(3),...,x(m)) 对应的矩阵为：

⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ x (1) 1 x (1) 2 ⋮ x (1) n x (2) 1 x (2) 2 ⋮ x (2) n \dots \dots \dots x (m) 1 x (m) 2 ⋮ x (m) n ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥

表示存在

m 个样本，每个样本有

n 个变量。在以后的使用中，称之为

x 。

现在有两个问题：
1. 激活函数是什么，如何选择？
2. w 和 b 如何计算出来？
在下面我们会解决这个问题。

1.1 激活函数（activation function）？

激活函数的作用是什么，可以参考：神经网络激励函数的作用是什么？有没有形象的解释？ - lee philip的回答 - 知乎

现常用的激活函数有：

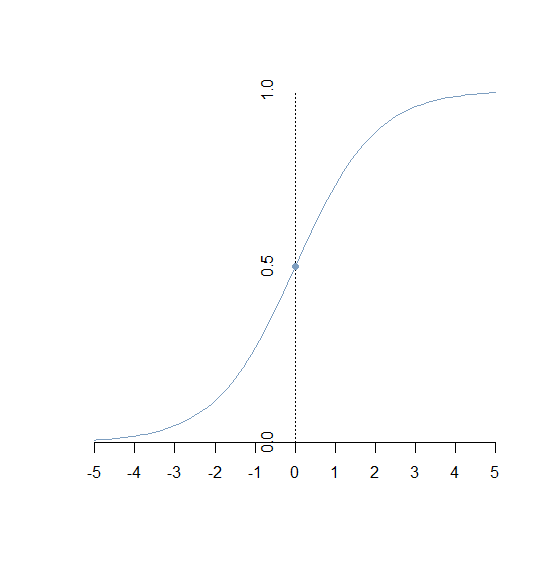
sigmoid函数：公式为 $y = 1 1 + e - x$ 图像为：
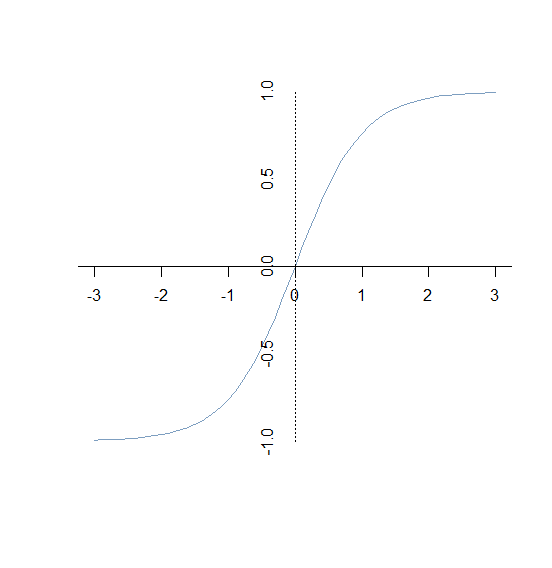
tanh函数：公式为 $y = s i n h ( x ) c o s h ( x ) = e x - e - x e x + e - x$ 图像为

ReLU函数：公式为 $y = m a x (0, x)$ 即： $i f (x < 0) : y = 0$ $i f (x > = 0) : y = x$ 图像为：

激活函数是要求定义域为 R ,且在定义域内处处可导的。对于上面的ReLu函数，在0的方，可以设置其导数为0或1。激活函数主要用来做线性变换，除非极特殊情况（例如：将输入加权求和后直接输出）是不会使用线性回归的。

在本文中，主要使用sigmoid函数，sigmoid函数又称为logistic函数,其函数形式为：

y = 1 1 + e - x

它主要用于二分分类，而二分分类就是将数据分为两类，例如：根据空气温度、湿度、云高等信息将天气分为晴天或非晴天。而他能够作为二分分类的一个非常重要的原因就是他的值域为

(0,1) ，正是由于这个特点，他可以将输入的参数能够很好的向概率映射。
另外当

x 远远大于0的时候，

y 会无限趋近于1;当

x 远远小于0的时候,

y 又无限趋近于0。

使用sigmoid进行二元分类的效果:

(图片来源：Logistic Regression – Geometric Intuition

1.2 梯度下降法

在说完了激活函数之后，我们还剩下一个问题如何确定 w 和 b 呢？因为我们之前并不知道 w 和 b ，因此需要使用样本来训练出 w 和 b 。我们使用梯度下降法来得到 w 和 b 。关于梯度下降法，可以参考一下文章:

机器学习中的数学(1)-回归(regression)、梯度下降(gradient descent)·LeftNotEasy
梯度下降法步长的取值范围·袁文彬
[Machine Learning]梯度下降法的三种形式BGD、SGD以及MBGD·POLL

梯度下降法的基本思路就是：先随机初始化一个 w 和 b 。然后根据该 w 和 b 求出相应的预测值 y^ ，在根据误差反向修正 w 和 b 。不断迭代使误差最小，来达到求出一个 w 和 b 使误差最小的目的。如下图所示：

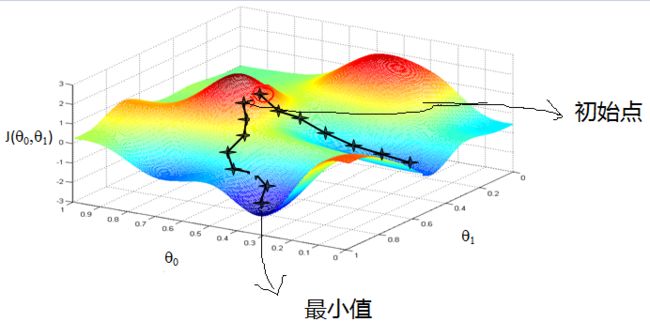
(图片来源：博客园)
在上图中，我们先初始化一个随机的 w 和 b ,当然此时的误差可能非常大。然后求 w 和 b 对误差的偏导，并向梯度下降的方向修正，随着不断的修正，误差会不断减小，当达到误差最小值时的 w 和 b 就是我们模型使用的参数。

1.2.1 初始化 w 和 b

在神经网络使用前需要先初始化 w 和 b 。

(1) w 的初始化
初始 w 一般采用随机初始化的方法,初始化的个数和前面传入参数的个数相同,例如，假设有三个传入参数 x1,x2,x3 那么初始化三个 w 则为：

import numpy
w = (numpy.random.random(3)*0.01).reshape(3,1)

[[ 0.00380803]
 [ 0.00945647]
 [ 0.00059899]]

一般在 w 初始化的过程中都会乘上0.01，使他小于0.01。这样做的目的是为了使 w 和 x 加权求和的结果较小，如果加权求和的结果很大，那么例如在sigmoid函数中，他的梯度会十分小，下降十分慢。

(2)b的初始化
而 b 的初始化就简单了，直接等于0就可以了，当然也可以随机初始化

1.2.2 正向传递

正向传递就是从前向后计算，其计算的过程为：

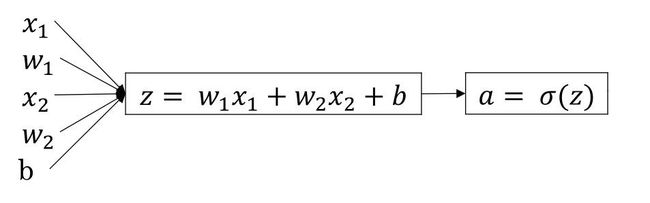
（图片来源：吴恩达神经网络课件）
计算过程也是相当简单，公式为：

z = w T x + b a = σ (z) = 1 1 + e - z

其中第一个公式是相加求和的过程，第二个公式是使用激活函数做线性变换的过程，在神经元中的计算就是这两步。

使用python编程如下：

from  sklearn  import datasets
import numpy as np
# 获取计算数据
iris = datasets.load_iris()
x = iris['data'][:100].T
y = iris['target'][:100].T
# 初始化w和b
np.random.seed(1)
w = (np.random.random(x.shape[0])*0.01).reshape(x.shape[0],1)
b = 0
# 正向传递
z = np.dot(w.T,x)+b
a = 1/(1+np.exp(-z))

输出a为：

array([[ 0.51176926,  0.5106609,  0.51081246,  0.51052831,  0.51184505,  0.51295288,  0.51114382,  0.51148511,  0.50995984,  0.51076538,  0.51244182,  0.51127673,  0.51048115,  0.50996,  0.51339837,  0.5141651,  0.51295277,  0.5118448,  0.51300994,  0.51238476,  0.51190196,  0.51228032,  0.51142814,  0.51163601,  0.51127682,  0.51076517,  0.51163622,  0.51187349,  0.51169348,  0.51081254,  0.51073675,  0.51205298,  0.51287778,  0.51344578,  0.51076538,  0.51112504,  0.51218602,  0.51076538,  0.51013982,  0.51158931,  0.51174058,  0.50905949,   0.51049983,  0.51196728,  0.51246041,  0.51063224,  0.51230925,  0.51070828,  0.51233763,  0.51130509,
 0.51411624,  0.51356665,  0.5139077 ,  0.51085794,  0.51295104,  0.51196642,  0.513718  ,  0.51018583,  0.51308412,  0.51134081,  0.50957006,  0.51268573,  0.51097233,  0.51263875,  0.51204194,  0.51362368,  0.51237325,  0.5116639 ,  0.5115586 ,  0.51117101,  0.51327242,  0.51238305,  0.51220285,  0.51230771,  0.51287567,  0.51333955,  0.51318812,  0.51367049,  0.51261004,  0.51137954,  0.51088678,  0.5108112 ,  0.51181492,  0.51232581,  0.51216486,  0.51358536,  0.51369929,  0.51169167,  0.51222206,  0.51121792,  0.51132248,  0.51281869,  0.51163497,  0.51011004,  0.51168215,  0.51225074,  0.51214631,  0.51266729,  0.51064972,  0.5119663 ]])

1.2.3 损失函数（Loss Function ）与成本函数（Cost Function ）

损失函数又叫做误差函数（error function）用来计算单个样本预测结果与实际结果的误差，存在数据 {(x(1)，y(1))，(x(2)，y(2))，⋯，(x(n)，y(n))} ,我们希望 y^=y ( y^ 表示预测值，即前面的 a )，误差在许多时候是无法消除的，而为了使预测值更接近于实际值，即 y^≈y ，而损失函数就是衡量预测值与真实值差别的函数

一般来说损失函数公式为：

L (y^， y) = 1 2 (y^- y) 2

损失函数是衡量单个训练样本的表现，而成本函数是整个训练样本的表现。成本函数公式为：

J (w, b) = 1 m \sum i = 1 m L (y^(i) ， y (i))

而我们的目的是选择出一个

w 和

b 来使成本函数

J(w，b) 最小。

但是对于sigmoid函数来说则不能使用这个损失函数函数，因为他对于sigmoid函数来说是一个非凸函数（虽然我试了半天也没有证明出来），存在许多极小值，有可能会陷入局部拟合状态，在网上经常会看到这样一张图：

我们的目的是使其全局最优，但是非凸函数往往会陷入到局部最优。

因为在神经网络的中使用的是梯度下降法（顺着梯度下降），因为对非凸函数做梯度下降时容易陷入局部拟合的特点，使用梯度下降法一般会避免非凸函数。因此对于sigmoid函数来说它将使用一个不同的损失函数，起到衡量误差的作用。其损失函数为：

L (y^， y) = - (y l o g y^+ (1 - y) l o g (1 - y^))

此时成本函数公式为：

J (w, b) = 1 m \sum i = 1 n L (y^(i) ， y (i)) = - 1 m \sum i = 1 m [y (i) l o g (y^(i)) + (1 - y (i)) l o g (1 - y^(i))]

1.2.4 误差反向传播

在上面提到，我们的目的是找到一个 w 和 b 的值来使成本函数 J(w,b) 的值最小，因此计算 J(w,b) 对 w 的偏导数为:

因为：

z = w 1 x 1 + w 2 x 2 + b y^= σ (z) = 1 1 + e - z L (y^， y) = - (y l o g y^+ (1 - y) l o g (1 - y^)) J (w, b) = 1 m \sum i = 1 n L (y^(i) ， y (i))

所以变量在损失函数上的偏导数为

\partial L ( y ^ ， y ) \partial w 当 w 为 w 1 时 = \partial ( - ( y l o g y ^ + ( 1 - y ) l o g ( 1 - y ^ ) ) ) \partial w = (- y y ^+ 1 - y 1 - y ^) \times \partial y ^ \partial w = (- y y ^+ 1 - y 1 - y ^) \times \partial ( 1 1 + e - z ) \partial w = (- y y ^+ 1 - y 1 - y ^) \times y^(1 - y^) \times \partial z \partial w = (- y y ^+ 1 - y 1 - y ^) \times y^(1 - y^) \times \partial ( w 1 x 1 + w 2 x 2 + b ) \partial w = (- y y ^+ 1 - y 1 - y ^) \times y^(1 - y^) \times x 1 = (y^- y) \times x 1

相应的

wi 时

∂L(y^，y)∂wi=(y^−y)×xi

b （可以看做其对应的

x=1 ）时

∂L(y^，y)∂b=y^−y

变量在成本函数上的偏导数为：

\partial J ( w i , b ) \partial w i = \partial ( 1 m \sum i = 1 n L ( y ^ ( i ) ， y ( i ) ) ) \partial w i = 1 m \sum i = 1 n \partial ( L ( y ^ ( i ) ， y ( i ) ) ) \partial w i = \sum i = 1 n ( y ^ - y ) \times x i m

因此

\partial J ( w i , b ) \partial w i = \sum i = 1 n ( y ^ - y ) \times x i m \partial J ( w i , b ) \partial b = \sum i = 1 n ( y ^ - y ) m

上面求出了成本函数在 w 上的偏导数，下面就可以对 w 和 b 进行修正，修正方式为原来的值减去一个学习率乘以偏导数的积，即使用下面的公式修正:
w ： w=w−α∂J(w,b)∂w
b ： b=b−αJ(w,b)
由于偏导数本身自带方向，因此在这里不需要考虑方向的问题。

对于学习率的选择一般在0-1之间，例如: 0.1,0.005,0.001,0.0005 等等。较大的学习率可以使梯度下降速度较快，能使模型更快的达到较好结果的位置，但是在最低点的时候会不断抖动，不易落到最低点,如下图所示：

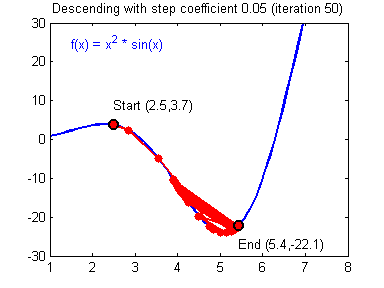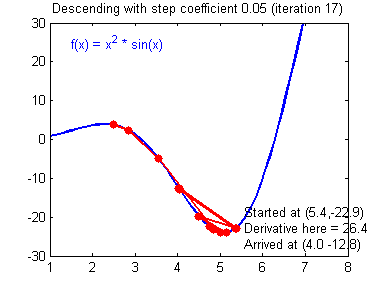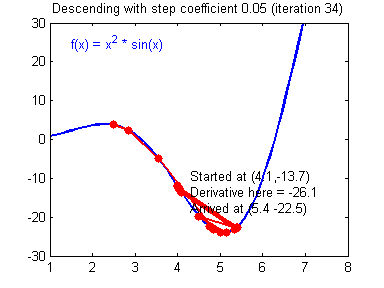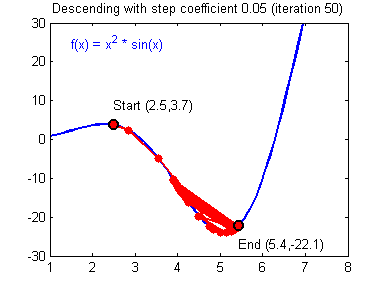
（图片来源：吴恩达神经网络作业）
而较小的学习率梯度下降速度慢，但是在最低点附近时候，能够较好的落到最低点附近，如下图所示：

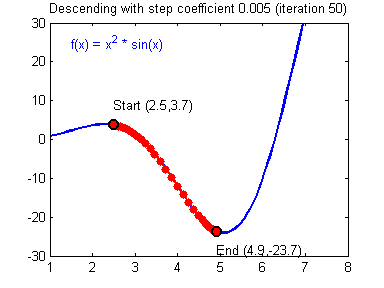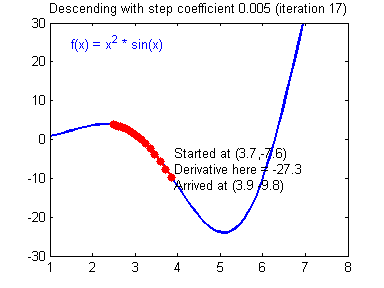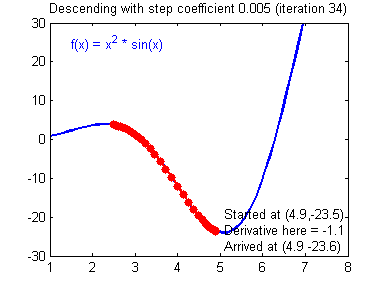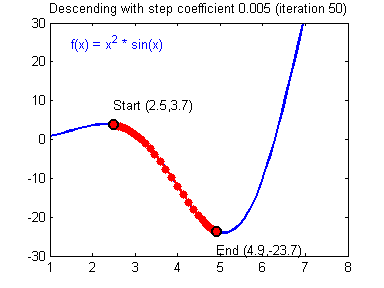
（图片来源：吴恩达神经网络作业）

现在也有许多方法来避免这个问题例如：学习率动态变化、基于惯性的梯度下降法等等。

1.3 公式总结

综上所述，在神经元训练的过程中会有三个过程:
(1)正向传递
总前向后计算，所用到的公式：

z = w T x + b y^= σ (z) = 1 1 + e - z

(2)计算误差
所用到的公式：

J (w, b) = - 1 m \sum i = 1 m [y (i) l o g (y^(i)) + (1 - y (i)) l o g (1 - y^(i))]

(3)反向传播
根据梯度下降法，从后向前反向修正

w 和

d w = \partial J ( w , b ) \partial w = x \cdot ( y ^ - y ) m d a = \partial J ( w i , b ) \partial b = y ^ - y m w = w - α \times d w b = b - α \times d b

使用python代码如下（采用鸢尾花数数据集）:

from  sklearn  import datasets
import numpy as np
# 获取计算数据
iris = datasets.load_iris()
x = iris['data'][:100].T
y = iris['target'][:100].T
m = x.shape[1]
alpat = 0.005
iterations_number = 20000
# 初始化w和b
np.random.seed(1)
w = (np.random.random(x.shape[0])*0.01).reshape(x.shape[0],1)
b = 0
for i in range(iterations_number):
    # 正向传递
    z = np.dot(w.T,x)+b
    a = 1/(1+np.exp(-z))
    # 计算误差
    J = - np.sum(y * np.log(a)+(1-y)*np.log(1-a))/m
    if(i%10000 == 0):
        print("当前迭代次数"+str(i)+"\t误差："+str(J))
    # 反向传递
    dw = np.dot(x,(a-y).T)/m
    db = np.sum(a-y)/m
    w = w - alpat*dw
    b = b - alpat*db

# 预测数据
z = np.dot(w.T,x)+b
a = 1/(1+np.exp(-z))
y_predict  = (a > 0.5 )+ 0

print("预测结果:"+str(y_predict)+"\n实际结果:"+str(y)+"\n预测准确率:"+str((1-np.sum(np.abs(y_predict-y))/m)*100)+"%")

输出结果：

当前迭代次数0 误差：0.69281000899
当前迭代次数10000 误差：0.0149878476054
预测结果:[[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
  0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
  1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]]
实际结果:[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
预测准确率:100.0%

2. 多层神经网络

有了上面神经元的概念，那么接下来的多层神经网络就比较好理解了，多层神经网络就是多个神经元所组成的网络。

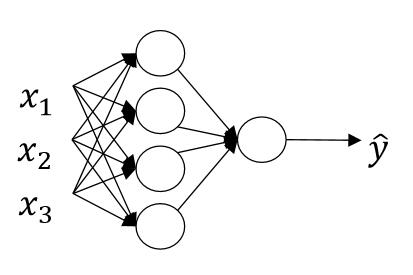
（图片来源：吴恩达神经网络课件
其实神经网络也很容易明白，即上一层节点的输出，等于下一层节点的输入。这里介绍几个概念“输入层”、“隐藏层”、“输出层”
在上图中， x1,x2,x3 是输入层，一般情况下输入层会被省略，在上图中也没有画出输入层节点；在中间的三个是“隐藏层”；最后面的一个圆是“输出层”。上图中没有画出输入层，只画出了一个输出层和一个隐藏层。

一个神经网络中必有一个输入层和一个输出层，有0个或多个隐藏层。输出层一般只有一个神经元，但是有时也会有多个输出因此有多个神经元。

我们现在做如下定义：上标“ [i] ”表示当前为第 i 层的节点，隐藏层为第0层忽略掉。上标“ (j) ”表示该层的第 j 个节点。因此上图中,

隐藏层节点的输入可以表示为 x[1]1,x[1]2,x[1]3 ；
隐藏层第一个节点的输入可以表示为 x[1](1)1,x[1](1)2,x[1](1)3 ；
隐藏层的第四个节点的输入可以表示为 x[1](4)1,x[1](4)2,x[1](4)3 ；
输出层的输入可以表示为 x[2]1,x[2]2,x[2]3,x[2]4 （由于只有一个输出层节点，因此有无上标是一样的）。

2.1 梯度下降法

2.1.1 正向传递

由上面定义得对于隐藏层第二个节点来说：输入为 x[1](2) ，权重 w[1](2) ，截距 b[1](2) ，输出 a[1](2) 。

他的正向传递计算公式为:

z [1] (2) = w [1] (2) T x [1] (2) + b [1] (2) a [1] (2) = σ (z [1] (2)) = 1 1 + e - z [ 1 ] ( 2 )

我们再抽象掉节点个数，即隐藏层公式来说：输入为

x[1] ，权重

w[1] ，截距

b[1] ，输出

a[1] 。
他的计算公式为:

z [1] = w [1] T x [1] + b [1] a [1] = σ (z [1]) = 1 1 + e - z [ 1 ]

因为上一层节点的输出等于下一层节点的输入，因此存在：

x[2]=a[1] ,因此上图中的输出层的计算可以表示为：

z [2] = w [2] T x [2] + b [2] = w [2] T a [1] + b [2] a [2] = σ (z [2]) = 1 1 + e - z [ 2 ]

因此，对于

x [1] = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ x (1) 1 x (1) 2 ⋮ x (1) n x (2) 1 x (2) 2 ⋮ x (2) n \dots \dots \dots x (m) 1 x (m) 2 ⋮ x (m) n ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ (上 标 " (i) " 表 示 第 i 个 样 本)

w [1] = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ w [1] (1) 1 w [1] (1) 2 ⋮ w [1] (1) n w [1] (2) 1 w [1] (2) 2 ⋮ w [1] (2) n \dots \dots \dots w [1] (p) 1 w [1] (p) 2 ⋮ w [1] (p) n ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥

b [1] = [b [1] (1) b [1] (2) \dots b [1] (p)]

可以求出

a [1] = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ a [1] (1) 1 a [1] (1) 2 ⋮ a [1] (1) p a [1] (2) 1 a [1] (2) 2 ⋮ a [1] (2) p \dots \dots \dots a [1] (m) 1 a [1] (m) 2 ⋮ a [1] (m) p ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥

而此层的

a 又是下一层的

x ，因此就可以向下计算。

所以上图中最后的公式为：

z [1] = w [1] T x [1] + b [1] a [1] = σ (z [1]) = 1 1 + e - z [ 1 ] x [2] = a [1] z [2] = w [2] T x [2] + b [2] a [2] = σ (z [2]) = 1 1 + e - z [ 2 ] y^= a [2]

对于更多的隐藏层来说，例如，隐藏层个数变为2，那么只需要不断地进行循环即可，即：

foriin1:L
z[i]=w[i]Tx[i]+b[i]
a[i]=σ(z[i])=11+e−z[i]
x[i+1]=a[i]
y^=a[i]

2.1.2 损失函数（Loss Function ）与成本函数（Cost Function ）

和神经元没什么区别…略

2.1.3 误差反向传播

误差反向就是反向推导回去，如果明白了上面的内容也并不难。
我们从后向前推导：
(1). 计算预测结果对误差的偏导数;
因为：

L (y^， y) = - (y l o g y^+ (1 - y) l o g (1 - y^)) J (w, b) = 1 m \sum i = 1 n L (y^(i) ， y (i))

所以：

\partial J ( w i , b ) \partial y ^= \partial ( 1 m \sum i = 1 n L ( y ^ ( i ) ， y ( i ) ) ) \partial y ^= 1 m \sum i = 1 n \partial ( L ( y ^ ( i ) ， y ( i ) ) ) \partial y ^= 1 m (- y y ^+ 1 - y 1 - y ^)

(2). 计算输出层权值对误差的偏导数;
因为：

\partial J ( w i , b ) \partial y ^= 1 m (- y y ^+ 1 - y 1 - y ^) y^= a [2] a [2] = σ (z [2]) = 1 1 + e - z [ 2 ] z [2] = w [2] T x [2] + b [2]

所以：

\partial J ( w i , b ) \partial w [ 2 ] = \partial y ^ \partial w [ 2 ] \times \partial J ( w i , b ) \partial y ^= ( a [ 2 ] - y ) T \cdot x [ 2 ] m

同理：

\partial J ( w i , b ) \partial b [ 2 ] = ( a [ 2 ] - y ) T m

(3). 修正输出层节点间的 w 和 b

w [2] ： w [2] = w [2] - α \partial J ( w , b ) \partial w [ 2 ] b [2] ： b [2] = b [2] - α J (w, b)

(4). 计算隐藏层的输出对误差的偏导数
因为：

\partial J ( w i , b ) \partial y ^= 1 m (- y y ^+ 1 - y 1 - y ^) y^= a [2] a [2] = σ (z [2]) = 1 1 + e - z [ 2 ] z [2] = w [2] T x [2] + b [2] x [2] = a [1]

所以：

\partial J ( w i , b ) \partial a [ 1 ] = \partial y ^ \partial a [ 1 ] \times \partial J ( w i , b ) \partial y ^= w [ 2 ] T \cdot ( a [ 2 ] - y ) m

(5). 计算隐藏层的权值对误差的偏导数
因为：

\partial J ( w , b ) \partial a [ 1 ] = w [ 2 ] T \times ( a [ 2 ] - y ) m z [1] = w [1] T x [1] + b [1] a [1] = σ (z [1]) = 1 1 + e - z [ 1 ]

所以：

\partial J ( w i , b ) \partial w [ 1 ] = \partial a [ 1 ] \partial w [ 1 ] \times \partial J ( w , b ) \partial a [ 1 ] = a [1] T (1 - a [1] T) \cdot x [1] \times \partial J ( w , b ) \partial a [ 1 ] T

(算不过来了...)
同理：

\partial J ( w i , b ) \partial b [ 1 ] = a [1] T (1 - a [1] T) \times \partial J ( w , b ) \partial a [ 1 ] T

(晕晕晕......快晕了......)

2.2 公式总结

好吧，我已经晕了，总结一下公式,上标“ [i] ”表示当前层的信息, L 表示隐藏层和输出层的共计个数。

(1)正向传递
总前向后计算，所用到的公式

foriin1:L
z[i]=w[i]Tx[i]+b[i]
a[i]=f(z[i])=σ(z[i])=11+e−z[i]
x[i+1]=a[i]
y^=a[i]