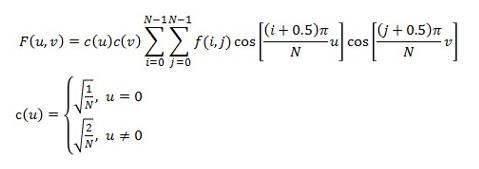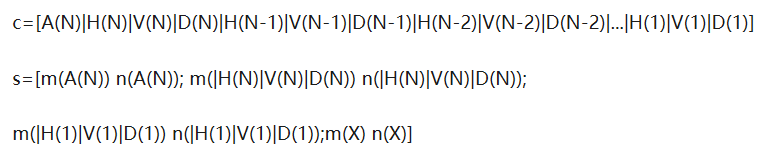DCT变换 / DWT变换 ----课堂笔记

之前也学过，但没有个具体总结，忘差不多了。

---

DCT变换
一、

DCT变换的全称是离散余弦变换（DCT），主要用于数据或者图像的压缩，由于DCT能够将空域的信号转换到频域上，因此具有良好的去相关性的性能。DCT变换本身是无损的且具有对称性。对原始图像进行离散余弦变换，变换后DCT系数能量主要集中在左上角，其余大部分系数接近于零。将变换后的DCT系数进行门限操作，将小于一定值系数归零，这就是图像压缩中的量化过程，然后进行逆DCT运算，可以得到压缩后的图像。

我们常见的JPEG静态图像编码以及MJPEG、MPEG动态编码等标准中都使用了DCT变换。

二、公式

二维DCT变换：

f(i,j)是原始的信号，F(u.v)是变换后的系数，N是原始图像的点数，此处为N*N，矩形时可改为N*M。

例如：（假如为N*M矩阵）F(0,0)=ΣΣf(i,j)  /   根号(N*M) 

二维DCT反变换：

三、dct变换的特征：

    一个图像的DCT低频系数分布在DCT系数矩阵的左上角,高频系数分布在右下角;

    低频系数的绝对值大于高频系数的绝对值;

    图像的低频部分集中了图像的大部分能量，鲁棒性强但不可见性差;

    图像的高频部分体现了图像的细节，不可见性强但鲁棒性差。

但并不是所有的二维矩阵都有这些特征。

四、问：为什么高频是次要的

DCT变换对图像进行压缩的原理是减少图像中的高频分量，高频主要是对应图像中的细节信息，而我们人眼对细节信息并不是很敏感，因此可以去除高频的信息量。另外，去掉50%的高频信息存储部分，图像信息量的损失不到5%。

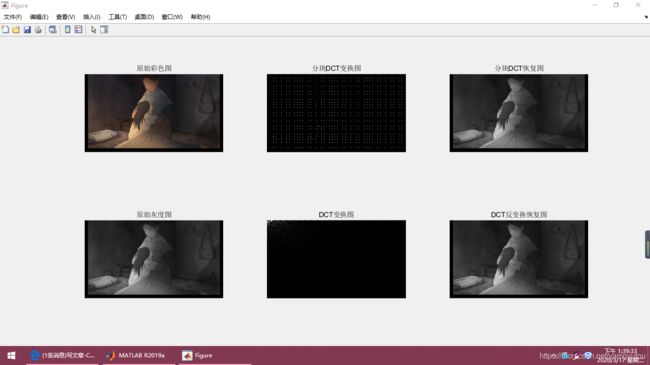
五、code and result

clc;
clear;

X=imread("youziyin.png");
X0=rgb2gray(X);

[a,b]=size(X0);
Y1=blkproc(X0,[8 8],'dct2');
X1=blkproc(Y1,[8 8],'idct2');

subplot(2,3,1);
imshow(uint8(X));
title('原始彩色图');

subplot(2,3,2);
imshow(uint8(Y1));
title('分块DCT变换图');

subplot(2,3,3);
imshow(uint8(X1));
title('分块DCT恢复图');
 
Y2=dct2(X0);
X2=idct2(Y2);

subplot(2,3,4);
imshow(uint8(X0));
title('原始灰度图');

subplot(2,3,5);
imshow(uint8(Y2));
title('DCT变换图');

subplot(2,3,6);
imshow(uint8(X2));
title('DCT反变换恢复图');

reference: https://www.cnblogs.com/wyuzl/p/7880124.html

八、基函数

https://www.h3399.cn/201803/564043.html

---

DWT变换

一、小波变换

搜狗百科介绍的小波：https://baike.sogou.com/v207283.htm?fromTitle=%E5%B0%8F%E6%B3%A2%E5%8F%98%E6%8D%A2

这三个也可以用来参考理解：

https://blog.csdn.net/shenziheng1/article/details/52973715

https://blog.csdn.net/carson2005/article/details/40981939

https://mp.weixin.qq.com/s?src=3×tamp=1586331975&ver=1&signature=ApxbrqJNHSesYNQ2UF1VYl3WwA0qgIacTPzCkimq1PHAoGAkMZ3SchwHYuOvcMxolyPugp3CvzE3WscMnHKr1xDOWnfuGIwUnqprUBmQt29cEjG6HoBxh9vzz5ojrXvUlO3gNS*vlzbWVOEF0rg1OzOLsHbpn2E7FNGXNp5U5m8=

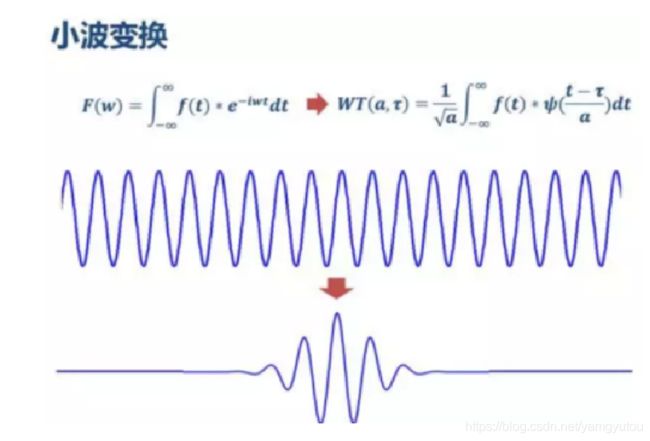
傅里叶变换可以得到信号的频域信息，小波变换可以得到时频信息（短时傅里叶变换也可得到这些信息）。小波可以实现正交化，短时傅里叶变换不能。 

对于突变信号，傅里叶变换会产生吉布斯效应，而衰减的小波会解决这一问题。

2D 小波变换

             

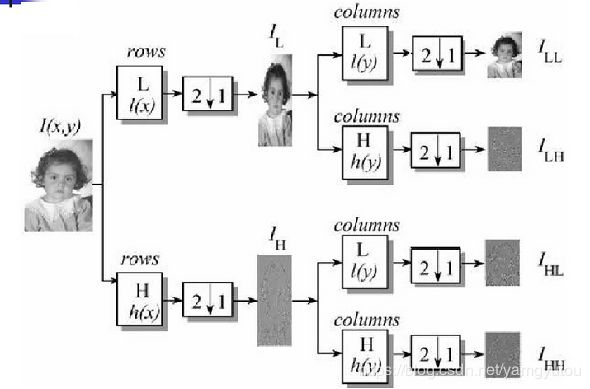
二、二维离散小波

A是低频信息，H是水平高频信息，V是垂直高频信息、D是对角高频信息。

一维haar小波

二维haar小波

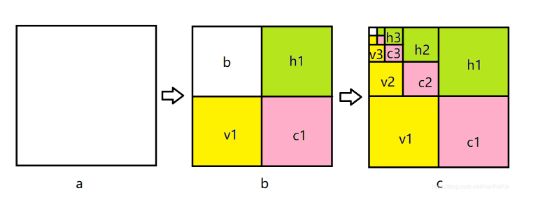
从水平和竖直两个方向进行高通和低通滤波，图a表示原图，图b表示经过一级小波变换的结果，h1 表示水平反向的细节，v1 表示竖直方向的细节，c1表示对角线方向的细节，b表示下2采样的图像。图c中表示继续进行Haar小波变换。

三、MATLAB实现

https://zhuanlan.zhihu.com/p/29482162

一层分解：

pic=imread('lena.jpg');
picg=rgb2gray(pic);
[cA,cH,cV,cD]=dwt2(picg,'haar');%使用haar小波

figure
imshow(picg);
title('原图');

figure
subplot(2,2,1);imshow(uint8(cA)),title('低频分量');
subplot(2,2,2);imshow(uint8(cH)),title('水平细节分量');
subplot(2,2,3);imshow(uint8(cV)),title('垂直细节分量');
subplot(2,2,4);imshow(uint8(cD)),title('对角线细节分量');

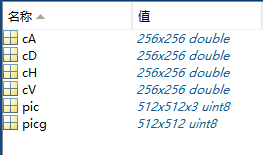
result:从工作区可以看出，生成的每个子图都变成了原图像的1/4大小。

    

两层分解：

[C,S]=wavedec2(X,N,'wname')%使用指定的小波基函数对矩阵X进行N层分解
[C,S]=wavedec2(X,N,Lo_D,Hi_D)%使用指定的低通滤波器Lo_D和高通滤波器Hi_D分解信号为N层；
                             %C为各层分解系数，S为各层分解系数的大小（行数及列数）

X0=imread('lena.jpg');
X=rgb2gray(X0);

[c,s]=wavedec2(X,2,'db1');%进行2尺度二维离散小波分解。分解小波函数-db1
[cH1,cV1,cD1]=detcoef2('all',c,s,1);%尺度1的所有方向的高频系数
[cH2,cV2,cD2]=detcoef2('all',c,s,2);%尺度2的所有方向的高频系数
cA1=appcoef2(c,s,'db1',1);%尺度1的低频系数
cA2=appcoef2(c,s,'db1',2);%尺度2的低频系数

figure;
subplot(3,3,1);imshow(X);title('原图');
subplot(3,3,2);imshow(uint8(cA1));axis off;title('尺度1的低频系数图像');
subplot(3,3,3);imshow(uint8(cA2));axis off;title('尺度2的低频系数图像');

figure;
subplot(3,3,4),imshow(uint8(cH1));axis off;title('尺度1水平方向高频系数');
subplot(3,3,5),imshow(uint8(cV1));axis off;title('尺度1垂直方向高频系数');
subplot(3,3,6),imshow(uint8(cD1));axis off;title('尺度1斜线方向高频系数');
subplot(3,3,7),imshow(uint8(cH2));axis off;title('尺度2水平方向高频系数');
subplot(3,3,8),imshow(uint8(cV2));axis off;title('尺度2垂直方向高频系数');
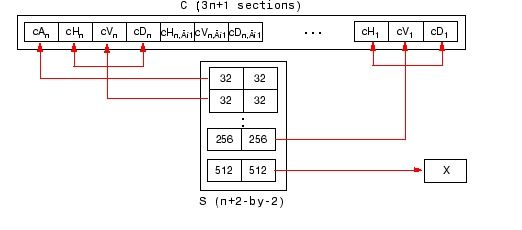
subplot(3,3,9),imshow(uint8(cD2));axis off;title('尺度2斜线方向高频系数');

result：进行一层分解后，对尺度一的低频系数图像继续分解得到尺度二的四个子图。

从工作区可以看到，一层子图是原图的1/4，二层子图是原图的1/16（也就是一层子图的1/4)

 

这是c和s的数据，因为原图512*512，所以c就是262144