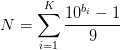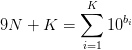AGC011_E Increasing Numbers （玄学贪心 或者 数学分析）

题意

定义：一个数是增长数，当且仅当它的每一位数字都不比左边一位数字小。

给出一个n位数Number，问最少用几个增长数才能表示出它（即把它拆成几个增长数的和的形式）。

算法1 玄学贪心

这是本蒟蒻莫名其妙yy出来的做法，感觉很有道理就去写了一下，没想到居然AC了？？

不过到现在还不能证明其正确性。只是在这里说下策略：

大胆猜想：每次减去最大的增长数可以保证次数最少。

试了几个样例，都是对的，而且这个做法本身也很有道理（以下都是瞎bb），因为减去最大的增长数后效果如下：

15624443-15599999=24444

实际上就是抹去了原数的前面若干位，并且让最后一位加1（如果大于9要进位）。

这样后面的关系影响很小，而且消去了尽可能多的位数。

而且这样可以轻松看出答案的上界是n，这个算法即使不是最优，那也十分接近最优答案了，至少它小于上界。

具体怎么实现呢？有点麻烦。我们发现每次操作相当于找到第一个位置i，满足a[i]>a[i+1]，以及最左边一个位置j，满足a[j..i]全相等，我们抹去a[1..j]，令a[j+1..len]这个数+1。这个用二分+树状数组维护一下即可。

复杂度。

算法2 数学分析

这才是正解，可以证明其正确性。不过这也太反人类了⑧……

我们定义形如111...111的数为“全一数”（特别地，0也是全一数）。

那么显然任何一个增长数都可以表示为9个全一数的和。

假设有最小的数K，使得N可以表示为K个全一数的和，那么答案显然就是。

所以我们的任务变成了求最小的K。这K个全一数分别为，其中。

观察下列等式：

记一个数x的各位数之和为d(x)，要想找到一组b使得上式成立，那么应有：d(9N+K)<=K（因为即使不进位，一个b[i]也只能使得数位和+1）。

事实上，满足了上述性质，我们显然可以构造出符合条件的b：多出来的b[i]全用0代替即可。

通过算法1我们已经得出了答案<=N，因此我们直接从小到大暴力枚举K，符合条件break即可。

复杂度。

 

我自己的代码是玄学贪心233：

#include 
#include 
#include 
#define rep(i,j,k) for (i=j;i<=k;i++)
using namespace std;
const int N=5e5+5;
int n,i,j,ans,top,lst,a[N],b[N],pre[N],tree[N];
char s[N];
void change(int x,int sgn) {
	while (x<=n) {	tree[x]+=sgn; x+=x&(-x); }
}
int query(int x) {
	int ret=0;
	if (x<1) return 0;
	while (x>0) { ret+=tree[x]; x-=x&(-x); }
	return ret;
}
void add() {
	int i,j;
	a[n]++; i=n;
	while (a[i]>9) a[i-1]++,a[i]=0,i--;
	rep(j,max(1,i-1),n) {
		if (b[j]>b[j+1]) change(j,-1);
		if (a[j]>a[j+1]) change(j,1);
		b[j]=a[j];
	}
	rep(j,i,n) if (a[j]==a[j-1]) pre[j]=pre[j-1]; else pre[j]=j;
}
int erfen(int x)
{
	int l=x,r=n,mid,sum,Prefix;
	Prefix=query(x-1);
	while (l>1;
		sum=query(mid);
		if (sum-Prefix>0) r=mid;
		else l=mid+1;
	}
	return l;
}
int main()
{
	scanf("%s",s+1);
	n=strlen(s+1);
	rep(i,1,n) a[i]=b[i]=s[i]-'0';
	rep(i,1,n) if (a[i]==a[i-1]) pre[i]=pre[i-1]; else pre[i]=i;
	
	rep(i,1,n) if (a[i]>a[i+1]) change(i,1);
	i=1;
	while (i<=n) {
		lst=i; i=erfen(i);
		ans++;
		if (i==n) break;
		lst=max(pre[i],lst);
		a[lst]=-1; i=lst+1;
		add();
	}
	printf("%d\n",ans);
	return 0;
}