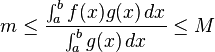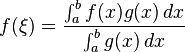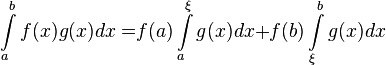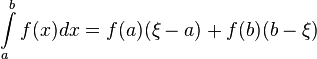中值定理
| 中值定理 | |
|---|---|
|
相关条目：微积分学 |
|
中值定理包括微分中值定理和积分中值定理。
目录
- 1 微分中值定理
- 1.1 罗尔中值定理
- 1.2 拉格朗日中值定理及正式叙述
- 1.3 柯西中值定理
- 2 积分中值定理
- 2.1 积分第一中值定理
- 2.1.1 证明
- 2.1.2 推论（拉格朗日中值定理的积分形式）
- 2.2 积分第二中值定理
- 2.2.1 内容
- 2.2.2 退化态的几何意义
- 2.1 积分第一中值定理
- 3 参见
微分中值定理
微分中值定理分为罗尔中值定理、拉格朗日中值定理和柯西中值定理，又（统）称为微分学基本定理、有限改变量定理或有限增量定理，是微分学的基本定理之一，内容是说一段连续光滑曲线中必然有一点，它的斜率与整段曲线平均斜率相同（严格的数学表达参见下文）。
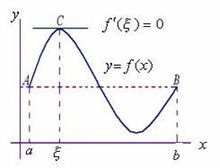
罗尔中值定理
如果函数 
满足
- 在闭区间
![[a,b]](http://img.e-com-net.com/image/info8/1f797ac36936491a925f70950a46c5a8.png)
上连续； - 在开区间
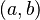内可导； - 在区间端点处的函数值相等，即
，
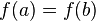那么在内至少有一点
，使得 
。这个定理称为罗尔定理。
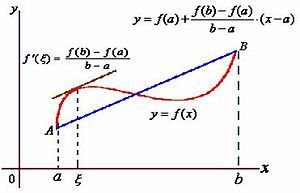
拉格朗日中值定理及正式叙述
令 ![f:[a,b]\rightarrow \mathbf R](http://img.e-com-net.com/image/info8/535b058dc4de40a38b46d4a7f3fe984a.png)
为闭区间 上的一个连续函数, 且在开区间 内可导, 其中 
那么在 上存在某个 
使得
此定理称为拉格朗日中值定理。拉格朗日中值定理是罗尔中值定理的推广，同时也是柯西中值定理的特殊情形。
这个定理在一个更一般的条件下仍然成立。只需假设 在 连续, 那么在 内对任意 
，极限
存在，为一个有限数字或者等于+∞或−∞. 如果有限, 则极限等于 . 定理的这个版本的应用的一个例子由从 到 
的实值三次方根函数映射给出 , 其导数在原点趋于无穷。
注意若一个可导函数是复变量的而不是实变量的，上面叙述的这个定理就不正确了。例如, 对全部实数 定义 
。那么
当 
时。
柯西中值定理
柯西中值定理, 也叫拓展中值定理, 是中值定理的一般形式。它叙述为: 如果函数f和g都在闭区间[a,b]上连续, 且在开区间(a, b)上可导, 那么存在某个c ∈ (a,b), 使得
当然, 如果g(a) ≠ g(b)并且g′(c) ≠ 0, 这等价于:
在几何上, 这表示曲线
![\begin{array}{ccc}[a,b]&\longrightarrow&\mathbb{R}^2\\t&\mapsto&\bigl(f(t),g(t)\bigr),\end{array}](http://img.e-com-net.com/image/info8/7d00ac7a636a46b1acfd5e360acd492a.png)
的图像存在平行于由(f(a),g(a))和(f(b),g(b))确定的直线的切线. 但柯西定理不能表明在任何情况下不同的两点(f(a),g(a))和(f(b),g(b))都存在切线, 因为可能存在一些 c值使f′(c) = g′(c) = 0, 换句话说取某个值时位于曲线的驻点; 在这些点似乎曲线根本没有切线. 下面是这种情形的一个例子
在区间[−1,1]上，曲线由(−1,0)到(1,0), 却并无一个水平切线; 然而它有一个驻点(实际上是一个尖点)在t = 0时。
柯西中值定理可以用来证明洛必达法则. (拉格朗日)中值定理是柯西中值定理当g(t) = t时的特殊情况.
积分中值定理
积分中值定理分为积分第一中值定理和积分第二中值定理，它们各包含两个公式。其退化状态均指在ξ的变化过程中存在一个时刻使两个图形的面积相等（严格表述在下面）。
积分第一中值定理
设 ![f:[a,b]\rightarrow \mathbb R](http://img.e-com-net.com/image/info8/26327bf65d444aab9d81cdfcba90b211.png)
为一连续函数，![g:[a,b]\rightarrow \mathbb R](http://img.e-com-net.com/image/info8/c7d5bbe90ba44080a54557ba4f72bb06.png)
要求g(x)是可积函数且在积分区间不变号，那么存在一点 ![\xi\in [a,b]](http://img.e-com-net.com/image/info8/f587b83216894e92a811f1abf2947d98.png)
使得
-
。
证明
在不失去一般性的条件下，设对所有x，g(x)≥0 ； 因为 
是闭区间上的连续函数， 取得最大值 
和最小值 
。于是
-
。
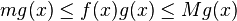对不等式求积分，我们有
-
。
若 
，则 
。
可取 上任一点。
若不等于零那么 
，
-
。
因为 
是连续函数，则必存在一点 ，使得
-
。
g(x)<0的情况按同样方法证明。
推论（拉格朗日中值定理的积分形式）
在上式中令
，则可得出：
设 为一连续函数，则∃，使
它也可以由拉格朗日中值定理推出：
设
在上可导，
，则∃，使
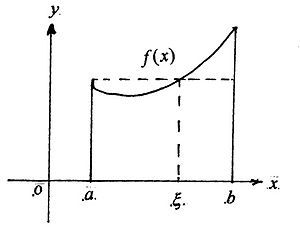
积分第二中值定理
积分第二中值定理与积分第一中值定理相互独立，却又是更精细的积分中值定理。它可以用来证明Dirichlet-Abel 反常 Rieman 积分判别法。
内容
若f,g在[a,b]上黎曼可积且f(x)在[a,b]上单调，则存在[a,b]上的点ξ使
-
；
退化态的几何意义
令g(x)=1，则原公式可化为：
-
；
进而导出：
-
；
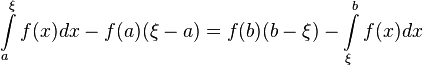此时易得其几何意义为： 能找到ξ∈[a,b]，使得S[红]+S[蓝]=S[阴影]， 即S[I]=S[II]
参见
- 罗尔定理
- 柯西中值定理
- 介值定理
- 极值定理
- 微积分
- 数学定理