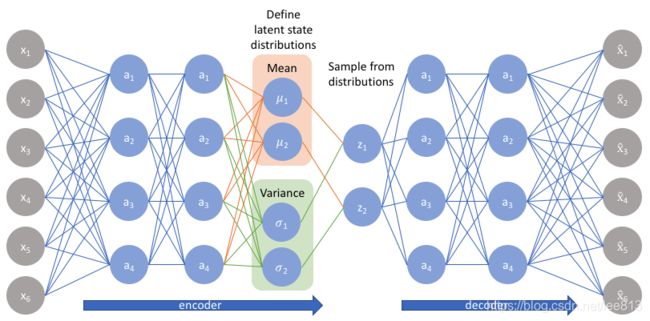
Variational Autoencoder 变分自动编码器

一步一步实现一个VAE

大部分来自Keras VAE的教程，不过没有使用mnist，而是用了cifar10的数据集

最简单的两个全链接层的Autoencoder

先贴个代码:

# this is the size of our encoded representations
encoding_dim = 32  # 32 floats -> compression of factor 24.5, assuming the input is 784 floats
# this is our input placeholder
input_img = Input(shape=(784,))
# "encoded" is the encoded representation of the input
encoded = Dense(encoding_dim, activation='relu')(input_img)
# "decoded" is the lossy reconstruction of the input
decoded = Dense(784, activation='sigmoid')(encoded)
# this model maps an input to its reconstruction
autoencoder = Model(input_img, decoded)
# this model maps an input to its encoded representation
autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')

这里就是把输入层放入一个全链接层，压缩成为一个32维的数组，然后再使用这个32维的数组用一个全链接层去还原原来的图片。
下面这段代码是用来显示效果，这里还是用的mnist的数据集。

encoder = Model(input_img, encoded)
# create a placeholder for an encoded (32-dimensional) input
encoded_input = Input(shape=(encoding_dim,))
# retrieve the last layer of the autoencoder model
decoder_layer = autoencoder.layers[-1]
# create the decoder model
decoder = Model(encoded_input, decoder_layer(encoded_input))

结果如下：

使用多层全链接层的Autoencoder

input_img = Input(shape=(784,))
encoded = Dense(128, activation='relu')(input_img)
encoded = Dense(64, activation='relu')(encoded)
encoded = Dense(32, activation='relu')(encoded)

decoded = Dense(64, activation='relu')(encoded)
decoded = Dense(128, activation='relu')(decoded)
decoded = Dense(784, activation='sigmoid')(decoded)


autoencoder = Model(input_img, decoded)
autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')

这里使用三层全链接层做encoder，三层做decoder，还是压缩到32维

效果好了一点点

深度卷积网络来构建的autoencoder

我们在这里用了cifar10作为数据集

input_img = Input(shape=(32, 32, 3))
x = Conv2D(64, (3, 3), padding='same')(input_img)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = MaxPooling2D((2, 2), padding='same')(x)
x = Conv2D(32, (3, 3), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = MaxPooling2D((2, 2), padding='same')(x)
x = Conv2D(16, (3, 3), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
encoded = MaxPooling2D((2, 2), padding='same')(x)

x = Conv2D(16, (3, 3), padding='same')(encoded)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = UpSampling2D((2, 2))(x)
x = Conv2D(32, (3, 3), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = UpSampling2D((2, 2))(x)
x = Conv2D(64, (3, 3), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = UpSampling2D((2, 2))(x)
x = Conv2D(3, (3, 3), padding='same')(x)
x = BatchNormalization()(x)
decoded = Activation('sigmoid')(x)

autoencoder = Model(input_img, decoded)
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')

输入为(32,32,3) 最后压缩到16维。

推理VAE的损失函数

条件： 我们有观察值X，这些值是从隐藏变量（Latent Variable Z）中推理出来的。Z则是从一个先验分布$p_{\theta }(z)$ 中获取的，$\theta$在这里并不知道，需要进行求解
根据贝叶斯定理我们有：
$$P(z|x)=\frac{P(x|z)P(z)}{P(x)}$$
但是边际似然函数$P_{\theta }(x)$是不可微的，所以我们不能评价或者对他进行求导，导致其不可倍积分。
边际似然函数求的是在$\theta$被积掉后，所求的变量的概率。
$$P_{\theta }(x)=\int p_{\theta }(x|z)p_{\theta }(z)dz$$
所以我们使用变分推断来估计这个分布, EM之类的算法就不适用了。
变分推断需要使用KL散度（KL divergence）即一种来测量两个概率分布的差别的测量。在变分推断中，我们要使用一个简单的分布来逼近真实的分布，而KL散度就是用来测量我们提供的分布跟真实分布差距大小的方法。即：
$$minKL(q(z|x)||p(z|x))$$

在VAE中，损失函数分为两部分，第一部分是KL散度的损失，他的作用像是一个范式一样来规范求出来的$\theta$。第二部分则是reconstruction error，即重建损失，是自动编码机中的损失，用来衡量建立网络的时候出现的损失。

Reparameterization trick

由于 z∼N(μ,σ)，我们应该从 N(μ,σ) 采样，但这个采样操作对 μ 和 σ 是不可导的，导致常规的通过误差反传的梯度下降法（GD）不能使用。通过 reparemerization，我们首先从 N(0,1) 上采样 ϵ，然后，z=σ⋅ϵ+μ。这样，z∼N(μ,σ)，而且，从 encoder 输出到 z，只涉及线性操作，（ϵ对神经网络而言只是常数），因此，可以正常使用梯度下降进行优化。

VAE 结构