语音信号的“短时时域”分析
语音信号的预处理
语音信号的频带范围通常是300~3400Hz,一般情况下取采样率为8kHz,本博客的部分代码采用的是已经数字化了的语音。
预加重
预加重的目的是为了对语音的高频部分进行加重,去除口唇辐射的影响,增加语音的高频分辨率。
一般通过使用一阶FIR高通数字滤波器来实现预加重,滤波器函数为:
$$H(z)=1-\alpha z^{-1}$$
其中$\alpha $为预加重系数,$0.9<\alpha<1.0$,
设n时刻的语音采样值为$x(n)$,经过预加重处理后的结果为$y(n)=x(n)-\alpha x(n-1)$,这里$\alpha=0.98$,
我们先来看看高通滤波器的幅频和相频响应:
clear; [h1,f1]=freqz([1,-0.98],[1],256,4000);%高通滤波器 pha=angle(h1); %高通滤波器的相位 H1=abs(h1); %高通滤波器的幅值 figure(1);subplot(211); plot(f1,H1);title('高通滤波器的幅频响应'); xlabel('频率/Hz');ylabel('幅度'); subplot(212);plot(pha);title('高通滤波器的相位响应'); xlabel('频率/Hz');ylabel('角度/radians');
原始语音信号和经过滤波后的语音信号
clear; fid=fopen('voice2.txt','rt'); %打开语音数字化文件 e=fscanf(fid,'%f'); %读数据 ee=e(200:455); %选取原始文件e的第200到455点的语音,也可选其他样点 figure(1);subplot(211);plot(ee);title('原始语音信号'); xlabel('样点数');ylabel('幅度'); axis([0 256 -3*10^4 2*10^4]); r=fft(ee,1024); %对信号ee进行1024点傅立叶变换 un=filter([1,-0.98],[1],ee); %un为经过高频提升后的时域信号 subplot(212);plot(real(un));title('经高通滤波后的语音信号'); xlabel('样点数');ylabel('幅度'); axis([0 256 -1*10^4 1*10^4]);
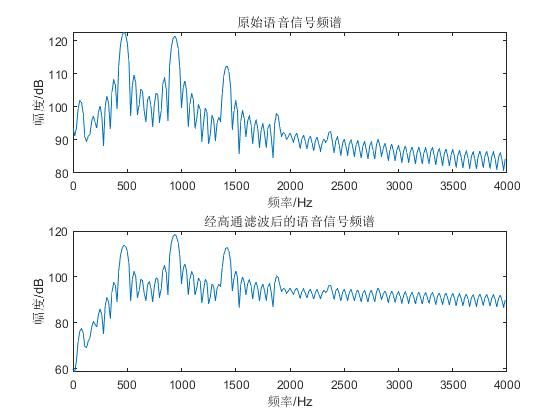
原始语音信号频率和经过滤波后的语音信号频率
clear; fid=fopen('voice2.txt','rt'); %打开语音数字化文件 e=fscanf(fid,'%f'); %读数据 ee=e(200:455); %选取原始文件e的第200到455点的语音,也可选其他样点 r=fft(ee,1024); %对信号ee进行1024点傅立叶变换 r1=abs(r); %对r取绝对值 r1表示频谱的幅度值 pinlv=(0:1:255)*8000/512; %点和频率的对应关系 yuanlai=20*log10(r1); %对幅值取对数 signal(1:256)=yuanlai(1:256);%取256个点,目的是画图的时候,维数一致 figure(1);subplot(211);plot(pinlv,signal);title('原始语音信号频谱'); xlabel('频率/Hz');ylabel('幅度/dB'); r2(1:256)=r(1:256); [h1,f1]=freqz([1,-0.98],[1],256,4000);%高通滤波器 u=r2.*h1'; % 将信号频域与高通滤波器频域相乘 相当于在时域的卷积 u2=abs(u); %取幅度绝对值 u3=20*log10(u2); %对幅值取对数 subplot(212);plot(pinlv,u3);title('经高通滤波后的语音信号频谱'); xlabel('频率/Hz'); ylabel('幅度/dB');
语音信号的加窗
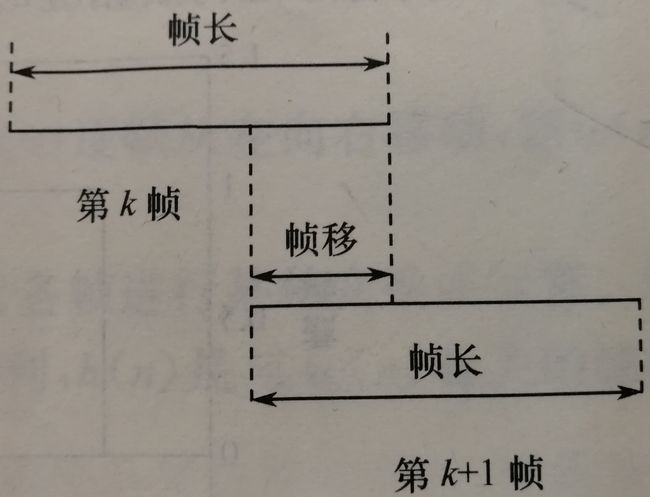
语音是随时间而变化的信号,但是语音在一小段时间内(10~30ms)语音信号近似看做平稳,即语音信号具有短时平稳特性。如此一来,可以把语音信号分为一些短段(分帧)来进行处理。语音信号的分帧是采用可移动的有限长度窗口进行加权的方法来实现的,一般每一秒的帧数为33`100帧,分帧时采用交叠分段的方法,使得帧与帧之间平滑过渡,保持其连续性,前一帧和后一帧的交叠部分称为帧移,帧移与帧长的比值一般取为0~1/2。
常用的窗有:
(1)、汉明(Hamming)窗
$$w(n)=w(n)=\left\{\begin{matrix}
0.54-0.64\cos [2\pi n/(N-1)]&&,0\leq n\leq N\\
0&&,其他
\end{matrix}\right.$$
汉明(Hamming)窗时域和频域波形,窗长N=62
% 汉明窗函数 x=linspace(20,80,61); %在20~80的横坐标间取61个值作为横坐标点 h=hamming(61); %取61个点的哈明窗值为纵坐标值 figure(1);subplot(1,2,1); plot(x,h,'k');title('Hamming窗时域波形'); %,k表示黑色 xlabel('样点数');ylabel('幅度'); w1=linspace(0,61,61); %取窗长内的61个点 w1(1:61)=hamming(61); %加哈明窗 w2=fft(w1,1024); %对时域信号进行1024点傅立叶变换 时域-->频域 w3=w2/w2(1); %幅度归一化 w4=20*log10(abs(w3)) %对归一化幅度取对数 w=2*[0:1023]/1024; %频率归一化 subplot(1,2,2);plot(w,w4,'k') %画幅度特性图 axis([0,1,-100,0]) %限定横、纵坐标范围 title('Hamming窗幅度特性'); %图标题 xlabel('归一化频率 f/fs');ylabel('幅度/dB');
(2)、矩形窗
$$w(n)=w(n)=\left\{\begin{matrix}
1&&,0\leq n\leq N-1\\
0&&,其他
\end{matrix}\right.$$
矩形窗的时域和频域波形,窗长61。
% 矩形窗函数 x=linspace(0,100,10001); %在0~100的横坐标间取10001个值 h=zeros(10001,1); %为矩阵h赋0值 h(1:2001)=0; %前2000个值取为0值 h(2002:8003)=1; %窗长 ,窗内值取为1 h(8004:10001)=0; %后2000个值取为0值 figure(1); %定义图号 subplot(1,2,1) %画第一个子图 plot(x,h,'k');title('矩形窗时域波形'); %画波形,横坐标为x,纵坐标为h,k表示黑色 xlabel('样点数'); ylabel('幅度'); axis([0,100,-0.5,1.5]) %限定横、纵坐标范围 line([0,100],[0,0]) %画出x轴 w1=linspace(0,61,61); %取窗长内的61个点 w1(1:61)=1; %赋值1,相当于矩形窗 w2=fft(w1,1024); %对时域信号进行1024点的傅立叶变换 w3=w2/w2(1) %幅度归一化 w4=20*log10(abs(w3)); %对归一化幅度取对数 w=2*[0:1023]/1024; %频率归一化 subplot(1,2,2); %画第二个子图 plot(w,w4,'k');title('矩形窗幅度特性'); %画幅度特性图 axis([0,1,-100,0]) %限定横、纵坐标范围 xlabel('归一化频率 f/fs');ylabel('幅度/dB');
矩形窗的主瓣宽度小于汉明窗,具有较高的频谱分辨率,但是矩形窗的旁瓣峰值较大,因此其频谱泄漏比较严重。相比,
汉明窗的主瓣宽度较宽,约大于矩形窗的一倍,但是它的旁瓣衰减较大,具有更平滑的低通特性,能够在较高的程度上反映短时信号的频率特性。
分帧