机器学习 --- GBDT提升算法（Gradient Boosting）

Gradient Boosting

以梯度为优化目标，以提升将整个架构串在一起，用决策树当做模型细节中的每一个小部分

分类回归树（CART）

数据集：$\left\{\begin{array}{c}((x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)}))\end{array}\right\}$

衡量标准：

$s^2\cdot m=(y^{(1_{left})}-{\bar{y}}_{left}{)}^2+...+(y^{(n_{left})}-{\bar{y}}_{left}{)}^2+(y^{(1_{right})}-{\bar{y}}_{right}{)}^2+...+(y^{(m-n_{left})}-{\bar{y}}_{right}{)}^2$

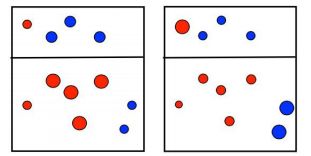
Adaboost算法概述

原数据集：

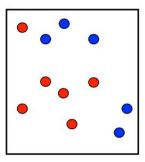
第一次划分：

在第一次划分完成后，对于分类正确的数据降低权重，分类错误的值增加权重

第二次划分：

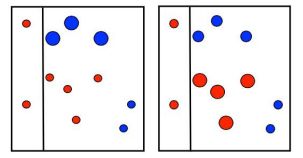
在第二次划分完成后，同样是对于分类正确的数据降低权重，分类错误的值增加权重

第三次划分：

在第三次划分完成后，同样是做权重调整工作

最终，对三次分类进行整合，不同的分类精度对应不同的 $\alpha$ 权重，将其加和得到最后结果

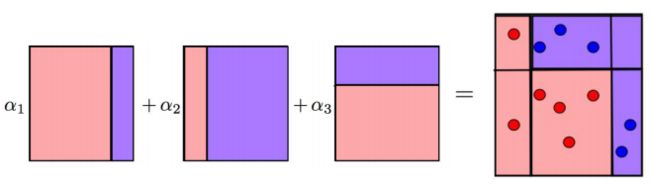
GB算法

优化的目标：
$$\underset{f(x)}{\mathrm{argmin}}{E}_{x,y}[L(y,f(x))]$$

$L(y,f(x))$是一个损失函数，$f(x)$ 是一个模型，我们需要找到一个模型 $f(x)$ 使得损失函数最小

其实目标还是去找最合适的参数：
$$\hat{\theta }=\underset{\theta }{\mathrm{argmin}}{E}_{x,y}[L(y,f(x,\theta ))]$$

结果依旧是需要迭代得出：
$$\hat{\theta }=\sum _{i=1}^M{\hat{\theta }}_i$$

梯度的思想

找到最合适的参数：
$$({\rho }_t,{\theta }_t)=\underset{\rho ,\theta }{\mathrm{argmin}}{E}_{x,y}[L(y,\hat{f}(x)+\rho \cdot h(x,\theta ))]$$

残差的计算（负梯度）：
$$r_{it}=-[\frac{\partial L(y,f(x_i))}{\partial f(x_i)}{]}_{f(x_i)=\hat{f}(x)}$$

参数迭代：
$${\theta }_t=\underset{\theta }{\mathrm{argmin}}\sum _{i=1}^n(r_{it}-h(x_i,\theta ){)}^2$$

步长的选择：
$${\rho }_t=\underset{\rho }{\mathrm{argmin}}\sum _{i=1}^{n}L(y_i,\hat{f}(x_i)+\rho \cdot h(x_i,{\theta }_t))$$

GBDT的工作流程${\left\{\begin{array}{c}(x_i,y_i)\end{array}\right\}}_{i=1,...,n}$

关于GBDT的工作流程，假设100个数据在一次训练迭代了三次模型，分别为 $f_1(x),f_2(x),f_3(x)$，第一个模型 $f_1(x)$ 拟合了 $80\%$ 的精度，那么在第二次拟合时，第二个模型 $f_2(x)$ 以剩下的 $20\%$ 的精度为基础继续进行训练拟合了 $18\%$ 的精度，第三个模型 $f_3(x)$ 继续以剩下的 $2\%$ 的精度进行训练，拟合掉了 $1\%$ ，那么到最后这三个模型就是以这样的拟合占比进行相加，得到最终 $99\%$ 正确率的结果

1. 初始化第一个方程：
   $$\hat{f}(x)={\hat{f}}_0,{\hat{f}}_0=\gamma ,\gamma \in R,{\hat{f}}_0=\underset{\gamma }{\mathrm{argmin}}L(y_i,\gamma )$$
2. 每次迭代都要计算残差：
   $$r_{it}=-[\frac{\partial L(y,f(x_i))}{\partial f(x_i)}{]}_{f(x_i)=\hat{f}(x)},i=1,...,n$$
3. 以残差为目标构建回归方程：
   $${\left\{\begin{array}{c}(x_i,r_{it})\end{array}\right\}}_{i=1,...,n}$$
4. 找到当前最合适的组合（遍历）：
   $${\rho }_t=\underset{\rho }{\mathrm{argmin}}\sum _{i=1}^{n}L(y_i,\hat{f}(x_i)+\rho \cdot h(x_i,{\theta }_t))$$
5. 经过M次迭代后的结果：
   $$\sum _{i=0}^M{\hat{f}}_i(x)$$

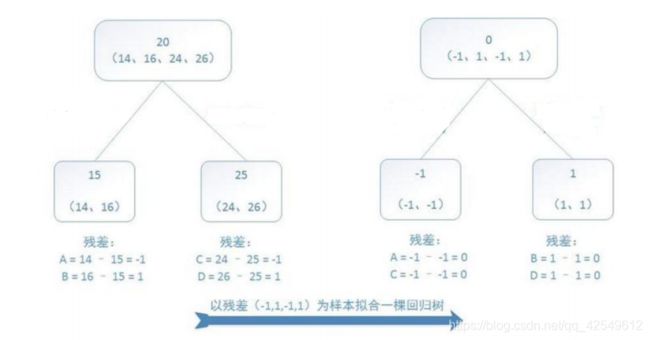
GBDT的回归任务

以这张图为例，在第一次回归后得到的残差，放入第二个回归树模型中再次进行回归任务
$$\begin{gathered} A的预测值=树1左节点（值15）+树2左节点（值-1）=14 \\ B的预测值=树1左节点（值15）+树2右节点（值-1）=16 \\ C的预测值=树1右节点（值25）+树2左节点（值-1）=24 \\ D的预测值=树1右节点（值25）+树2右节点（值-1）=26 \end{gathered}$$

GBDT的分类任务

分类与回归任务均使用CART，原理和多分类的逻辑回归类似，使用GBDT得到类别的概率值，对应进行分类。比如一个三分类问题，我们可以训练3颗树（分别表示是不是第一类，是不是第二类，是不是第三类）

分类任务实例

假设当前样本属于第二类（第一轮，输入的为真实值）：$\{\begin{array}{c}{f}_{11}(x)=0-f_1(x)\\ f_{22}(x)=1-f_1(x)\\ f_{33}(x)=0-f_1(x)\end{array}$

第二轮输入：$(x,f_{11}(x)),(x,f_{22}(x)),(x,f_{33}(x))$

最后进行归一化
$$p_2=\frac{exp(f_1(x))}{{\sum }_{k=1}^{3}exp(f_k(x))}$$

可视化解释

1. Gradient Boosting explained
2. Gradient Boosting Interactive Playground

GBDT、Xgboost、LightGBM对比

Mnist数据集识别

使用Sklearn的GBDT

GradientBoostingClassifier
GradientBoostingRegressor

import gzip
import pickle as pkl
from sklearn.model_selection import train_test_split
# 读文件划分数据集
def load_data(path):
    f = gzip.open(path, 'rb')
    try:
        #Python3
        train_set, valid_set, test_set = pkl.load(f, encoding='latin1')
    except:
        #Python2
        train_set, valid_set, test_set = pkl.load(f)
    f.close()
    return(train_set,valid_set,test_set)

path = 'mnist.pkl.gz' 
train_set,valid_set,test_set = load_data(path)

Xtrain,_,ytrain,_ = train_test_split(train_set[0], train_set[1], test_size=0.9)
Xtest,_,ytest,_ = train_test_split(test_set[0], test_set[1], test_size=0.9)
print(Xtrain.shape, ytrain.shape, Xtest.shape, ytest.shape)

参数说明：

• learning_rate: The learning parameter controls the magnitude of this change in the estimates. (default=0.1)
• n_extimators: The number of sequential trees to be modeled. (default=100)
• max_depth: The maximum depth of a tree. (default=3)
• min_samples_split: Tthe minimum number of samples (or observations) which are required in a node to be considered for splitting. (default=2)
• min_samples_leaf: The minimum samples (or observations) required in a terminal node or leaf. (default=1)
• min_weight_fraction_leaf: Similar to min_samples_leaf but defined as a fraction of the total number of observations instead of an integer. (default=0.)
• subsample: The fraction of observations to be selected for each tree. Selection is done by random sampling. (default=1.0)
• max_features: The number of features to consider while searching for a best split. These will be randomly selected. (default=None)
• max_leaf_nodes: The maximum number of terminal nodes or leaves in a tree. (default=None)
• min_impurity_decrease: A node will be split if this split induces a decrease of the impurity greater than or equal to this value. (default=0.)

实例测试：

from sklearn.ensemble import GradientBoostingClassifier
import numpy as np
import time 
# 实例化
clf = GradientBoostingClassifier(n_estimators=10, 
                                 learning_rate=0.1, 
                                 max_depth=3)
# 开始训练，记录时间
start_time = time.time()
clf.fit(Xtrain, ytrain)
end_time = time.time()
print('The training time = {}'.format(end_time - start_time))
# 预测与评价
pred = clf.predict(Xtest)
accuracy = np.sum(pred == ytest) / pred.shape[0]
print('Test accuracy = {}'.format(accuracy))

The training time = 27.277734518051147
Test accuracy = 0.815

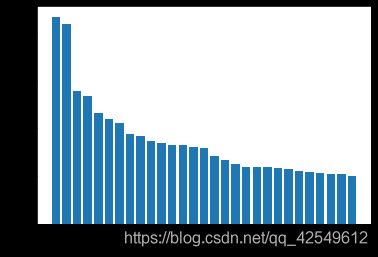
集成算法可以得出特征重要性，这里画图看一下

import matplotlib.pyplot as plt
# 得到特征重要性结果 画图
plt.hist(clf.feature_importances_)

一般情况下，我们还要根据特征重要性进行筛选，将有用的特征保留

from collections import OrderedDict
# 选出重要性>0.01的特征
d = {}
for i in range(len(clf.feature_importances_)):
    if clf.feature_importances_[i] > 0.01:
        d[i] = clf.feature_importances_[i]
# 重要性排序
sorted_feature_importances = OrderedDict(sorted(d.items(), key=lambda x:x[1], reverse=True))
D = sorted_feature_importances
# 画图
rects = plt.bar(range(len(D)), D.values(), align='center')
plt.xticks(range(len(D)), D.keys(),rotation=90)
plt.show()

XGBoost

XGBoost 加入了更多的剪枝策略和正则项，控制过拟合风险。传统的GBDT用的是CART，Xgboost能支持的分类器更多，也可以是线性的。GBDT只用了一阶导，但是xgboost对损失函数做了二阶的泰勒展开，并且还可以自定义损失函数。

Xgboost参数.

import xgboost as xgb
import numpy as np
import time

# 数据读入Xgboost DMatrix格式
dtrain = xgb.DMatrix(Xtrain, label=ytrain)
dtest = xgb.DMatrix(Xtest, label=ytest)

# 通过映射指定参数
params = {
    'booster':'gbtree',     #  tree-based models
    'objective': 'multi:softmax', 
    'num_class':10, 
    'eta': 0.1,             # Same to learning rate in GBDT
    'gamma':0,              # Similar to min_impurity_decrease in GBDT
    'alpha': 0,             # L1 regularization term on weight (analogous to Lasso regression)
    'lambda': 2,            # L2 regularization term on weights (analogous to Ridge regression)
    'max_depth': 3,         # Same as the max_depth of GBDT
    'subsample': 1,         # Same as the subsample of GBDT
    'colsample_bytree': 1,  # Similar to max_features in GBM
    'min_child_weight': 1,  # minimum sum of instance weight (Hessian) needed in a child
    'nthread':1,            # default to maximum number of threads available if not set
}
num_round = 10

# 开始训练，记录时间
start_time = time.time()
bst = xgb.train(params, dtrain, num_round)
end_time = time.time()
print('The training time = {}'.format(end_time - start_time))

# 预测与评价
ypred = bst.predict(dtest)
accuracy = np.sum(ypred == ytest) / ypred.shape[0]
print('Test accuracy = {}'.format(accuracy))

The training time = 15.998175859451294
Test accuracy = 0.827

LightGBM

LightGBM 中文文档

优点：

• 更快的训练效率

• 低内存使用

• 更好的准确率

• 支持并行学习

• 可处理大规模数据

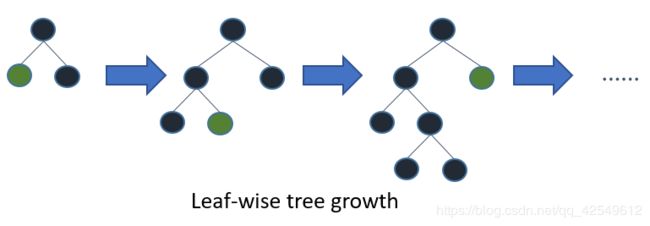
它摒弃了现在大部分GBDT使用的按层生长（level-wise）的决策树生长策略，使用带有深度限制的按叶子生长（leaf-wise）的策略。level-wise过一次数据可以同时分裂同一层的叶子，容易进行多线程优化，也好控制模型复杂度，不容易过拟合。但实际上level-wise是一种低效的算法，因为它不加区分的对待同一层的叶子，带来了很多没必要的开销，因为实际上很多叶子的分裂增益较低，没必要进行搜索和分裂。

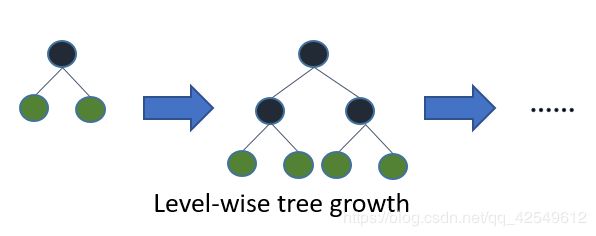
Leaf-wise则是一种更为高效的策略，每次从当前所有叶子中，找到分裂增益最大的一个叶子（不按层级），然后分裂，如此循环。因此同Level-wise相比，在分裂次数相同的情况下，Leaf-wise可以降低更多的误差，得到更好的精度。Leaf-wise的缺点是可能会长出比较深的决策树，产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度的限制，在保证高效率的同时防止过拟合。

import lightgbm as lgb
train_data = lgb.Dataset(Xtrain, label=ytrain)
test_data = lgb.Dataset(Xtest, label=ytest)

# 通过映射指定参数
params = {
    'num_leaves':31,                # Same to max_leaf_nodes in GBDT, but GBDT's default value is None
    'max_depth': -1,                # Same to max_depth of xgboost
    'tree_learner': 'serial', 
    'application':'multiclass',     # Same to objective of xgboost
    'num_class':10,                 # Same to num_class of xgboost
    'learning_rate': 0.1,           # Same to eta of xgboost
    'min_split_gain': 0,            # Same to gamma of xgboost
    'lambda_l1': 0,                 # Same to alpha of xgboost
    'lambda_l2': 0,                 # Same to lambda of xgboost
    'min_data_in_leaf': 20,         # Same to min_samples_leaf of GBDT
    'bagging_fraction': 1.0,        # Same to subsample of xgboost
    'bagging_freq': 0,
    'bagging_seed': 0,
    'feature_fraction': 1.0,         # Same to colsample_bytree of xgboost
    'feature_fraction_seed': 2,
    'min_sum_hessian_in_leaf': 1e-3, # Same to min_child_weight of xgboost
    'num_threads': 1
}
num_round = 10

# 开始训练，记录时间
start_time = time.time()
bst = lgb.train(params, train_data, num_round)
end_time = time.time()
print('The training time = {}'.format(end_time - start_time))

# 预测与评价
ypred_onehot = bst.predict(Xtest)
ypred = []
for i in range(len(ypred_onehot)):
    ypred.append(ypred_onehot[i].argmax())

accuracy = np.sum(ypred == ytest) / len(ypred)
print('Test accuracy = {}'.format(accuracy))

The training time = 7.425395488739014
Test accuracy = 0.888

结果对比

	time(s)	accuracy(%)
GBDT	27.28	0.815
XGBoost	16.00	0.827
LightGBM	7.43	0.888

LightGBM 实例 — 饭店流量预测

预处理数据

客流量数据表

import pandas as pd
# 读取数据
air_visit = pd.read_csv('air_visit_data.csv')
# 整合数据 按天计算
air_visit = air_visit.groupby('air_store_id').apply(lambda g: g['visitors'].resample('1d').sum()).reset_index()
# 缺失值填充 0
air_visit['visit_date'] = air_visit['visit_date'].dt.strftime('%Y-%m-%d')
air_visit['was_nil'] = air_visit['visitors'].isnull()
air_visit['visitors'].fillna(0, inplace=True)

日期数据表

import pandas as pd
# 读取数据
date_info = pd.read_csv('date_info.csv')
# 更改列名
date_info.rename(columns={'holiday_flg': 'is_holiday', 'calendar_date': 'visit_date'}, inplace=True)
# shift()操作对数据进行移动，可以观察前一天和后天是不是节假日
# 前一天是否为假期
date_info['prev_day_is_holiday'] = date_info['is_holiday'].shift().fillna(0)
# 后一天是否为假期
date_info['next_day_is_holiday'] = date_info['is_holiday'].shift(-1).fillna(0)

地区数据表

import pandas as pd
# 读取数据
air_store_info = pd.read_csv('air_store_info.csv')

测试集制作

import numpy as np
# 读取数据
submission = pd.read_csv('sample_submission.csv')
submission['air_store_id'] = submission['id'].str.slice(0, 20)
submission['visit_date'] = submission['id'].str.slice(21)
# 建立测试集标签
submission['is_test'] = True
submission['visitors'] = np.nan
submission['test_number'] = range(len(submission))

对所有数据信息进行汇总

data = pd.concat((air_visit, submission.drop('id', axis='columns')))

处理空值

# 'is_test' 的空值填充 False
data['is_test'].fillna(False, inplace=True)
# 在'visit_date'列上进行 merge，left 按照left的dataframe为基准，右边值为空的话就默认nan
data = pd.merge(left=data, right=date_info, on='visit_date', how='left')
# 在'air_store_id'列上进行 merge，left 按照left的dataframe为基准，右边值为空的话就默认nan
data = pd.merge(left=data, right=air_store_info, on='air_store_id', how='left')
data['visitors'] = data['visitors'].astype(float)

天气数据表

import glob

weather_dfs = []
# 遍历 .csv 数据文件 拿到数据
for path in glob.glob('./1-1-16_5-31-17_Weather/*.csv'):
    weather_df = pd.read_csv(path)
    # 拿到地区ID
    weather_df['station_id'] = path.split('\\')[-1].rstrip('.csv')
    weather_dfs.append(weather_df)
# 数据拼接
weather = pd.concat(weather_dfs, axis='rows')
# 重命名
weather.rename(columns={'calendar_date': 'visit_date'}, inplace=True)

用不同地区的数据求出每天的平均气温

# 求不同日期的平均气温和平均降水量
means = weather.groupby('visit_date')[['avg_temperature', 'precipitation']].mean().reset_index()
# 重命名
means.rename(columns={'avg_temperature': 'global_avg_temperature', 'precipitation': 'global_precipitation'}, inplace=True)
# 连接
weather = pd.merge(left=weather, right=means, on='visit_date', how='left')
# 缺失值用平均值填充
weather['avg_temperature'].fillna(weather['global_avg_temperature'], inplace=True)
weather['precipitation'].fillna(weather['global_precipitation'], inplace=True)

离群点筛选

异常点问题，数据中存在部分异常点，以正太分布为出发点，认为95%的是正常的，所以选择了1.96这个值。对异常点来规范，让特别大的点等于正常中最大的

# 找到离群点
def find_outliers(series):
    return (series - series.mean()) > 1.96 * series.std()
# 做截断操作
def cap_values(series):
    outliers = find_outliers(series)
    max_val = series[~outliers].max()
    series[outliers] = max_val
    return series
    
stores = data.groupby('air_store_id')
data['is_outlier'] = stores.apply(lambda g: find_outliers(g['visitors'])).values
data['visitors_capped'] = stores.apply(lambda g: cap_values(g['visitors'])).values
# log变换 
data['visitors_capped_log1p'] = np.log1p(data['visitors_capped'])

日期特征

data['is_weekend'] = data['day_of_week'].isin(['Saturday', 'Sunday']).astype(int)
data['day_of_month'] = data['visit_date'].dt.day

特征提取

# 针对周六、日构造新特征
data['is_weekend'] = data['day_of_week'].isin(['Saturday', 'Sunday']).astype(int)
# 转换为 datatime格式
data['visit_date'] = pd.to_datetime(data['visit_date'])
# 获取日期
data['day_of_month'] = data['visit_date'].dt.day

指数加权移动平均(Exponential Weighted Moving Average)，反应时间序列变换趋势，需要我们给定alpha值，这里我们来优化求一个最合适的（一方面考虑前一项因素的影响，另一方面是）
$$D_2=\alpha D1+(1-\alpha )D_1$$

from scipy import optimize

# 计算指数加权移动平均值
def calc_shifted_ewm(series, alpha, adjust=True):
    return series.shift().ewm(alpha=alpha, adjust=adjust).mean()

# 找最优 alpha
def find_best_signal(series, adjust=False, eps=10e-5):
    
    def f(alpha):
        shifted_ewm = calc_shifted_ewm(series=series, alpha=min(max(alpha, 0), 1), adjust=adjust)
        corr = np.mean(np.power(series - shifted_ewm, 2))
        return corr
     
    res = optimize.differential_evolution(func=f, bounds=[(0 + eps, 1 - eps)])
    
    return calc_shifted_ewm(series=series, alpha=res['x'][0], adjust=adjust)

roll = data.groupby(['air_store_id', 'day_of_week']).apply(lambda g: find_best_signal(g['visitors_capped']))
data['optimized_ewm_by_air_store_id_&_day_of_week'] = roll.sort_index(level=['air_store_id', 'visit_date']).values

roll = data.groupby(['air_store_id', 'is_weekend']).apply(lambda g: find_best_signal(g['visitors_capped']))
data['optimized_ewm_by_air_store_id_&_is_weekend'] = roll.sort_index(level=['air_store_id', 'visit_date']).values

roll = data.groupby(['air_store_id', 'day_of_week']).apply(lambda g: find_best_signal(g['visitors_capped_log1p']))
data['optimized_ewm_log1p_by_air_store_id_&_day_of_week'] = roll.sort_index(level=['air_store_id', 'visit_date']).values

roll = data.groupby(['air_store_id', 'is_weekend']).apply(lambda g: find_best_signal(g['visitors_capped_log1p']))
data['optimized_ewm_log1p_by_air_store_id_&_is_weekend'] = roll.sort_index(level=['air_store_id', 'visit_date']).values

这里再尽可能多的提取时间序列信息

def extract_precedent_statistics(df, on, group_by):
    
    df.sort_values(group_by + ['visit_date'], inplace=True)
    
    groups = df.groupby(group_by, sort=False)
    
    stats = {
        'mean': [],
        'median': [],
        'std': [],
        'count': [],
        'max': [],
        'min': []
    }
    
    exp_alphas = [0.1, 0.25, 0.3, 0.5, 0.75]
    stats.update({'exp_{}_mean'.format(alpha): [] for alpha in exp_alphas})
    
    for _, group in groups:
        
        shift = group[on].shift()
        roll = shift.rolling(window=len(group), min_periods=1)
        
        stats['mean'].extend(roll.mean())
        stats['median'].extend(roll.median())
        stats['std'].extend(roll.std())
        stats['count'].extend(roll.count())
        stats['max'].extend(roll.max())
        stats['min'].extend(roll.min())
        
        for alpha in exp_alphas:
            exp = shift.ewm(alpha=alpha, adjust=False)
            stats['exp_{}_mean'.format(alpha)].extend(exp.mean())
    
    suffix = '_&_'.join(group_by)
    
    for stat_name, values in stats.items():
        df['{}_{}_by_{}'.format(on, stat_name, suffix)] = values


extract_precedent_statistics(
    df=data,
    on='visitors_capped',
    group_by=['air_store_id', 'day_of_week']
)

extract_precedent_statistics(
    df=data,
    on='visitors_capped',
    group_by=['air_store_id', 'is_weekend']
)

extract_precedent_statistics(
    df=data,
    on='visitors_capped',
    group_by=['air_store_id']
)

extract_precedent_statistics(
    df=data,
    on='visitors_capped_log1p',
    group_by=['air_store_id', 'day_of_week']
)

extract_precedent_statistics(
    df=data,
    on='visitors_capped_log1p',
    group_by=['air_store_id', 'is_weekend']
)

extract_precedent_statistics(
    df=data,
    on='visitors_capped_log1p',
    group_by=['air_store_id']
)

# One Hot 特征提取
data = pd.get_dummies(data, columns=['day_of_week', 'air_genre_name'])

Lightgbm建模

数据集划分

# 拿到标签
data['visitors_log1p'] = np.log1p(data['visitors'])
# 拿到训练集
train = data[(data['is_test'] == False) & (data['is_outlier'] == False) & (data['was_nil'] == False)]
# 拿到测试集
test = data[data['is_test']].sort_values('test_number')
# 删除不需要的指标
to_drop = ['air_store_id', 'is_test', 'test_number', 'visit_date', 'was_nil',
           'is_outlier', 'visitors_capped', 'visitors',
           'air_area_name', 'latitude', 'longitude', 'visitors_capped_log1p']
train = train.drop(to_drop, axis='columns')
train = train.dropna()
test = test.drop(to_drop, axis='columns')
# 数据集
X_train = train.drop('visitors_log1p', axis='columns')
X_test = test.drop('visitors_log1p', axis='columns')
y_train = train['visitors_log1p']

建模

import lightgbm as lgbm
from sklearn import metrics
from sklearn import model_selection

np.random.seed(42)
# 参数设定
model = lgbm.LGBMRegressor(
    objective='regression', # 目标函数
    max_depth=5, # 树最大深度
    num_leaves=25, #叶子节点个数
    learning_rate=0.007, # 学习率
    n_estimators=1000, 
    min_child_samples=80, 
    subsample=0.8,
    colsample_bytree=1,
    reg_alpha=0,
    reg_lambda=0,
    random_state=np.random.randint(10e6)
)
# 交叉验证
n_splits = 6
cv = model_selection.KFold(n_splits=n_splits, shuffle=True, random_state=42)

val_scores = [0] * n_splits

sub = submission['id'].to_frame()
sub['visitors'] = 0

feature_importances = pd.DataFrame(index=X_train.columns)

for i, (fit_idx, val_idx) in enumerate(cv.split(X_train, y_train)):
    
    X_fit = X_train.iloc[fit_idx]
    y_fit = y_train.iloc[fit_idx]
    X_val = X_train.iloc[val_idx]
    y_val = y_train.iloc[val_idx]
    # 训练
    model.fit(
        X_fit,
        y_fit,
        eval_set=[(X_fit, y_fit), (X_val, y_val)],
        eval_names=('fit', 'val'),
        eval_metric='l2',
        early_stopping_rounds=200,
        feature_name=X_fit.columns.tolist(),
        verbose=False
    )
    
    val_scores[i] = np.sqrt(model.best_score_['val']['l2'])
    # 结果相加
    sub['visitors'] += model.predict(X_test, num_iteration=model.best_iteration_)
    feature_importances[i] = model.feature_importances_
    
    print('Fold {} RMSLE: {:.5f}'.format(i+1, val_scores[i]))
# 求均值
sub['visitors'] /= n_splits
# log反变换
sub['visitors'] = np.expm1(sub['visitors'])

val_mean = np.mean(val_scores)
val_std = np.std(val_scores)

print('Local RMSLE: {:.5f} (±{:.5f})'.format(val_mean, val_std))

输出结果查看

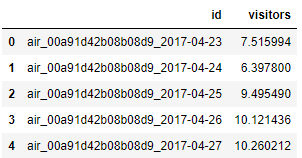
sub.to_csv('result.csv', index=False)
import pandas as pd
df = pd.read_csv('result.csv')
df.head()