动态规划!!!动态规划!!!
我一定要把动态规划搞定!!!
0、动态规划必备知识:
http://www.hawstein.com/posts/dp-novice-to-advanced.html
1、最长非降子序列的长度
(这是属于一维动态规划的问题)
题目:一个序列有N个数:A[1],A[2],…,A[N],求出最长非降子序列的长度。
思路:dp[i]表示前i个数中以A[i]结尾的最长非降子序列的长度;想要求dp[i],就把i前面的各个子序列中, 最后一个数不大于A[i]的序列长度加1,然后取出最大的长度即为dp[i]。最有数组dp[]中最大的数,即为最长非降子序列的长度。
代码:
import java.util.Scanner;
public class Solution {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while(sc.hasNext()){
int n = sc.nextInt();
int[] A = new int[n];
for(int i=0; iint result = 1;
//dp[i]表示前i个数中以A[i]结尾的最长非降子序列的长度
int[] dp = new int[n];
for(int i=0; i1;
//把i前面的各个子序列中, 最后一个数不大于A[i]的序列长度加1,然后取出最大的长度即为dp[i]
for(int j=0; jif(A[j]1);
}
}
result = Math.max(result, dp[i]);
}
System.out.println(result);
}
}
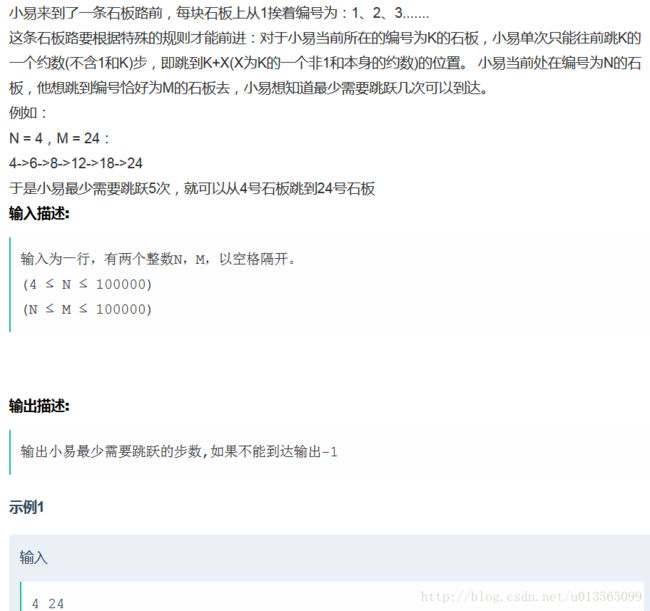
} 2、跳石板
思路:https://www.nowcoder.com/questionTerminal/4284c8f466814870bae7799a07d49ec8
代码:
import java.util.Scanner;
public class Solution {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while(sc.hasNext()){
int N = sc.nextInt();
int M = sc.nextInt();
int[] dp = new int[100001];
for(int i=N; i<=M; i++){
dp[i] = Integer.MAX_VALUE; //表示不可到达
}
dp[N] = 0;
for(int i=N; iif(dp[i]==Integer.MAX_VALUE){
continue;
}
//计算约数
for(int j=2; j*j<=i; j++){
if(i%j==0){
if((i+j)<=M){
dp[i+j] = Math.min(dp[i+j], dp[i]+1);
}
if((i+i/j)<=M){
dp[i+i/j] = Math.min(dp[i+i/j], dp[i]+1);
}
}
}
}
int result = -1;
if(dp[M]!=Integer.MAX_VALUE){
result = dp[M];
}
System.out.println(result);
}
}
} 3、直方图包含的最大面积

(参考: http://blog.csdn.net/li563868273/article/details/51121169)
代码:
public int countArea(int[] A, int n) {
int[][] dp = new int[n][n];
//初始值
for(int i=0; ifor(int k=1; kfor(int i=0; (i+k)//得到该区间的最小值
int min = A[i];
for(int j=i; j<=(i+k); j++){
min = ((A[j]<min)?A[j]:min);
}
//比较3种情况,得到最大值
dp[i][i+k] = Math.max(dp[i+1][i+k], dp[i][i+k-1]);
dp[i][i+k] = Math.max(min*(k+1), dp[i][i+k]);
}
}
return dp[0][n-1];
} 4、路径问题
思路:(参考“必备知识”中的二维DP问题)
代码:
public int countPath(int[][] map, int n, int m) {
int startX = 0;
int startY = 0;
int endX = 0;
int endY = 0;
for(int i=0; ifor(int j=0; jif(map[i][j] == 1){
startX = j;
startY = i;
}else if(map[i][j] == 2){
endX = j;
endY = i;
}
}
}
//确定方向
int dirX = (startX1 : -1);
int dirY = (startY1 : -1);
int[][] count = new int[n][m];
count[startY][startX] = 1;
//确定竖边界的初始值
for(int i=startY+dirY; i!=(endY+dirY); i+=dirY){
if(map[i][startX]==-1){
count[i][startX] = 0;
}else{
count[i][startX] = count[i-dirY][startX];
}
}
//确定横边界的初始值
for(int j=startX+dirX; j!=(endX+dirX); j+=dirX){
if(map[startY][j]==-1){
count[startY][j] = -1;
}else{
count[startY][j] = count[startY][j-dirX];
}
}
for(int i=startY+dirY; i!=(endY+dirY); i+=dirY){
for(int j=startX+dirX; j!=(endX+dirX); j+=dirX){
if(map[i][j]==-1){
count[i][j] = 0;
}else{
count[i][j] = count[i-dirY][j] + count[i][j-dirX];
}
}
}
return count[endY][endX];
} 5、合唱团
题目来源:网易2017
https://www.nowcoder.com/practice/661c49118ca241909add3a11c96408c8?tpId=85&tqId=29830&tPage=1&rp=1&ru=/ta/2017test&qru=/ta/2017test/question-ranking
解题思路:
http://blog.csdn.net/fcxxzux/article/details/52138964
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while(sc.hasNext()){
int n = sc.nextInt();
int[] a = new int[n+1];
for(int i=1; i<=n; i++){
a[i] = sc.nextInt();
}
int k = sc.nextInt();
int d = sc.nextInt();
//dpMax[i][j]表示以第i个人为最后一个,已经选择了j个人了
long[][] dpMax = new long[n+1][k+1];
long[][] dpMin = new long[n+1][k+1];
long result = 0;
for(int i=1; i<=n; i++){
dpMax[i][1] = dpMin[i][1] = a[i];
for(int j=2; j<=k; j++){
if(i0;
}else{
for(int m=i-1; m>=Math.max(i-d, 1); m--){
dpMax[i][j] = Math.max(dpMax[i][j], Math.max(dpMax[m][j-1]*a[i], dpMin[m][j-1]*a[i]));
dpMin[i][j] = Math.min(dpMin[i][j], Math.min(dpMax[m][j-1]*a[i], dpMin[m][j-1]*a[i]));
}
}
}
result = Math.max(result, dpMax[i][k]);
}
System.out.println(result);
}
}
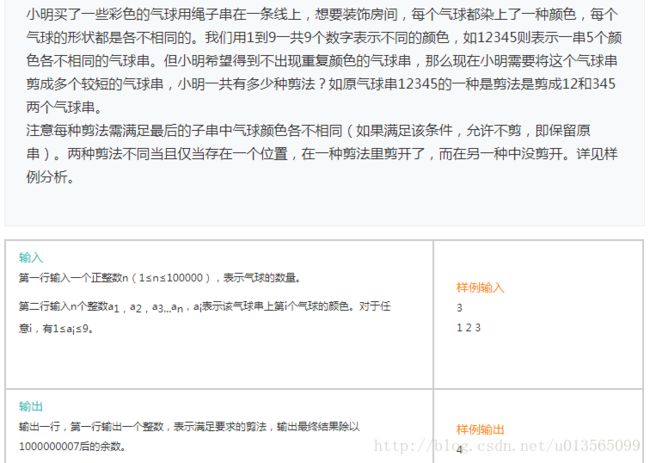
} 6、剪气球
题目来源:http://exercise.acmcoder.com/quesexcuse?paperId=213
思路:在计算dp[i+1]时,我们需要考虑第i+1个数可以和前面哪些数分到一起组成连续的子数组。(参考:http://blog.csdn.net/jacky_chenjp/article/details/63684427)
代码:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while(sc.hasNext()){
int n = sc.nextInt();
int[] a = new int[n];
for(int i=0; iint[] dp = new int[n+1];
dp[0] = 1;
for(int i=1; i<=n; i++){
int[] count = new int[10];
for(int j=i-1; j>=0; j--){
count[a[j]]++;
if(count[a[j]]>1){
break;
}else{
dp[i] = (dp[i]+dp[j])%1000000007;
}
}
}
System.out.println(dp[n]);
}
}
}