深入理解计算机系统(第三版)第6章 家庭作业
若有错误,还望各位不吝赐教~
6.22
由题意可知:
每条磁道位数 = 2 * Π * x * r
假设每单位的长度为一个磁道
则总的磁道数 = r - x * r
故有磁盘容量 = 2 * Π * r * r * x * (1 - x)
故当x = 1/2时,磁盘有最大容量
6.23
由图可知:
Tavg seek = 4 ms
由公式可得:
Tavg rotation = 1/2 Tmax rotation = 1/2 * 60s / 15000RPM * 1000ms/s = 2 ms
Tavg transfer = 60 / 15000RPM * 1/ 800扇区/磁道 * 1000ms/s = 0.005 ms
故有 Tavg access = Tavg seek + Tavg rotation + Tavg transfer = 4 ms + 2 ms + 0.005 ms = 6.005 ms
6.24
这个文件由4000个(近似值)512字节的逻辑块组成。
由公式可知:Tmax rotation = 4 ms, Tavg rotation = 2 ms
由图可知: Tavg seek = 4 ms
A:最好情况:在好情况中,块被映射到连续的扇区,在同一柱面上,那样就可以一块接一块地读,不用移动读/写头。一旦读/写头定位到了第一个扇区,需要磁盘转四整圈(每圈1000个扇区)来读所有4000个块。所以,读这个文件的总时间 = Tavg seek + Tavg rotation + Tmax rotation * 4 = 4 ms + 2 ms + 4 * 4 ms = 22 ms
B: 随机的情况:在这种情况中,块被随机的映射到扇区上,读4000个块中的每一块都需要Tavg seek + Tavg rotation ms,所以读这个文件的总时间为(Tavg seek + Tavg rotation ) * 4000 = 24000 ms
[注]:和习题6.4一样
6.25
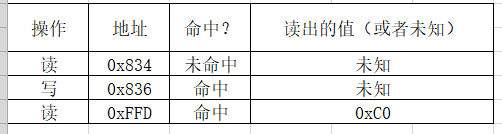
6.26
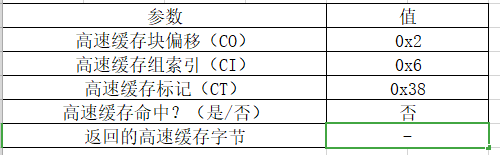
6.27
A:
当标记位为45时,
C0 = 00, 01, 10, 11(分别对应字节0~3)
CI = 001
CT = 01000101
故有 0x08A4, 0x08A5, 0x08A6, 0x08A7。
同理可得:当标记位为38时,
CO = 00, 01, 10, 11
CI = 001
CT = 00111000
故有 0x0704, 0x0705, 0x0706, 0x0707
B:
组6中命中的只有标记位为91
故
C0 = 00, 01, 10, 11
CI = 110
CT = 10010001
可得: 0x1238, 0x1239, 0x123A, 0x123B
6.28
A:
组2中没有命中的
B:
组4中,当标记位为C7时
CO = 00, 01, 10, 11
CI = 100
CT = 11000111
故有 0x18F0,0x18F1, 0x18F2, 0x18F3
当标记位为05时
CO = 00, 01, 10, 11
CI = 100
CT = 00000101
故有 0x00B0, 0x00B1, 0x00B2, 0x00B3
C:
组5中只有标记位为71的命中
CO = 00, 01, 10, 11
CI = 101
CT = 01110001
故有 0x0E34, 0x0E35, 0x0E36, 0x0E37
D:
组7中只有标记位为DE的命中
CO = 00, 01, 10, 11
CI = 111
CT = 11011110
故有 0x1BDC, 0x1BDD, 0x1BDE, 0x1BDF
6.29
A:

【注】:中文版书上说地址宽12位,但是给出了13位地址。不知道是机械工业出版社的老毛病(错误)还是故意这样出题,结合B中给出的地址也是12位,故为上图
6.30
A: C = E * B * S = 4 * 4 * 8 = 128字节
B:
6.31
[注]: 注意有效位(书上有提示!)
6.32
6.33
由图可知,组2中命中的只有标记位为BC, B6
当标记位为BC时,
CO = 00, 01, 10, 11
CI = 010
CT = 10111100
故有 0x1788, 0x1789, 0x178A, 0x178B
当标记位为B6时
CO = 00,01, 10, 11
CI = 010
CT = 10110110
故有 0x16C8, 0x16C9, 0x16CA, 0x16CB
6.34
6.35
6.36
A:由于x[0]的地址为0,x[1]的地址为512,每次都会替换块,故不命中率为100%
B: 当高速缓存的大小为1024字节时,不会发生替换,只剩下每块的冷不命中,故不命中率为25%
C:两路组相联就相当于一个块可以存8个4字节,使用LRU替换策略,就相当于每次存8个4字节的时候只有刚开始的一个4字节冷不命中,故不命中率为12.5%(我的理解,就是数组第一行先存8个后,数组第2行不会替换,而是存在接下来可存的8个4字节中,当把缓存存满后,从上到下依次替换。如果有错误,希望大佬能给我纠正一下,万分感激。因为有的答案说还是25%)
D:不能,冷不命中是无法避免的
E:能,因为在读总数不变的情况下,更大的块会减少冷不命中的次数
6.37

来说一下N=60,BC的情况 S = C / (E * B) = 4096 / (1 * 16) = 256
给256个块取号从0~255
对于N=60,函数B来说,它的访问顺序为0, 15, 30, 45, 60…255,14,29,44,59…254, 13, 28, 43, 58…254, 12, 27, 42, 57, 72, 87, 102, 117
这是访问a[0][0]到a[60][0]全不命中,但是访问a[0][1],a[0][2],a[0][3]全命中,推广可知:不命中率为25%
函数C也是类似
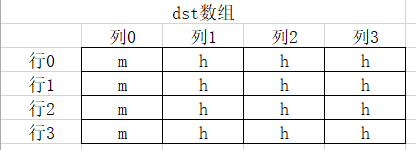
6.38
A: 16 * 16 * 4 = 1024
B: 1024 / 8 = 128
C: 128 / 1024 = 12.5%
6.39
A: 1024
B: 1024 / 4 = 256
C:25%
6.40
A: 1024
B: 256
C: 25%
6.41
25%
6.42
25%
6.43
100%
6.44
略
6.45 6.46
不会。。。