PAT 甲级 1010 Radix
前排提示:本题目在牛客网上的数据较弱,建议到PAT官网(即PTA)上作答
题目简介

给定两个数,其中一个数N1知道其进制r,另一个N2不知道。求N2在几进制下,和N1相等?
例如 6,110,已知6是十进制数据,问什么时候6==110?显然,是在110为二进制时。
输入描述
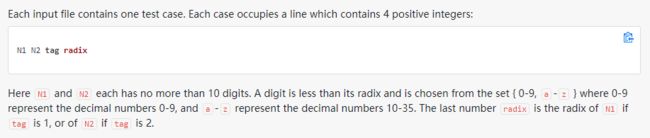
N1、N2是输入的两个数,tag代表是哪一个数是已知进制的,radix是进制数。
坑点: 虽然题目中说明a-z表示10-35,但是这只用在N1、N2的表示中!!!意思就是说,如果输入的radix是11进制,radix将表示为11,而不是b!!——这就又引出一个隐含的信息,radix的大小可能超过36。
这代表着,radix的大小可能非常大(比如9999,2147483647……),但是N1、N2中的每一位数字大小却不会超过35。
同理,你的输出中,是用十进制表示的进制数,可能超过36。
实际上(题目不知道为什么没表明 ),radix的大小最大可达到C语言中long long的数据上限,因此不仅要采用long long来记录,而且要谨防超限。
(N1、N2最长10位,想象一下一个最大值:9223372036854775807进制数zzzzzzzzzz,数据一定会爆炸)
输出描述
输入样例1
6 110 1 10
输出样例1
2
输入样例2
1 ab 1 2
输出样例2
Impossible
题目分析
上面分析了数据很大,首先考虑一下两点:
1、优先采用Java实现,因为Java有BigInteger类,可以表示、运算任意大小的数(据说内存有多大,数就能有多长)
2、匹配的时候不能用遍历。比如输入是
10 999999999 1 999999999
我们要计算999999999在几进制下等于 999999999进制下的10,我们不能从2进制、3进制、4进制……等逐个试起(想象一下上限是9223372036854775807进制),而应该采用二分查找。
代码如下:
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStream;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.math.BigInteger;
import java.util.StringTokenizer;
public class Main {
static final int BUFFER_SIZE = 8192 * 25;
static BufferedReader br;
static StringTokenizer tokenizer;
static void initInput(InputStream in) throws Exception {
br = new BufferedReader(new InputStreamReader(in), BUFFER_SIZE);
tokenizer = new StringTokenizer("");
}
static String next() throws Exception {
while (!tokenizer.hasMoreTokens()) {
tokenizer = new StringTokenizer(br.readLine());
}
return tokenizer.nextToken();
}
static int nextInt() throws Exception {
return Integer.parseInt(next());
}
static PrintWriter pw;
/*将一个radix进制下的数valStr转化为10进制下的表示*/
public static BigInteger converts(String valStr, BigInteger radix) {
char[] valArr = valStr.toCharArray();
BigInteger sum = BigInteger.ZERO;
for (int i = 0; i < valArr.length; i++) {
//将字符串每一位的数值转化为10进制表示
int v = valArr[i] - '0'< 10 ? valArr[i] - '0' : valArr[i] - 'a'+10;
if (radix.compareTo(BigInteger.valueOf(v)) < 0)
return BigInteger.valueOf(Long.MAX_VALUE);
sum = sum.multiply(radix).add(BigInteger.valueOf(v));
}
return sum;
}
public static void main(String[] args) throws Exception {
initInput(System.in);
pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out), BUFFER_SIZE));
/*所有数值都要采用字符串存储,因为BigInteger最常用的构造方法是用字符串直接构造*/
String a = next(), b = next();
int tag = nextInt();
String radix = next();
/*为了方便处理,把已知进制的数设为N1,未知进制的数设为N2*/
String N1 = tag == 1 ? a : b;
String N2 = tag == 1 ? b : a;
/*N1的实际值*/
final BigInteger N1Int = converts(N1, new BigInteger(radix));
/*二分查找的下限,应该是N2每一位中出现过的数字中最大值+1,
比如一个数“177”,它最小是8进制的,而不可能是7进制或更小。
*/
int maxBit = 0;
for (int i = 0; i < N2.length(); i++) {
char ch = N2.charAt(i);
int val = (ch >= '0' && ch <= '9') ? ch - '0' : ch - 'a' + 10;
maxBit = Math.max(val, maxBit);
}
BigInteger start = BigInteger.valueOf(maxBit + 1);
BigInteger end = N1Int.compareTo(start) < 0 ? start : N1Int;
BigInteger res = null;
while (end.compareTo(start) >= 0) {
/*注意在BigInteger中取中点的方法,divide()是除法的意思*/
BigInteger mid = start.add(end).divide(BigInteger.valueOf(2));
/*N2在mid进制下的值*/
BigInteger midTenVal = converts(N2, mid);
if (midTenVal.compareTo(N1Int) >= 0) {
/*当N2在mid进制下的值等于N1的值时,考虑mid进制和res进制的大小,
如果res为null,代表mid是第一个符合条件的进制,则将mid赋给res,
或者mid进制比res小,也可以采用(题目中说了多个答案满足取最小)*/
if (midTenVal.compareTo(N1Int) == 0 && (res == null || mid.compareTo(res) < 0))
res = mid;
end = mid.subtract(BigInteger.valueOf(1));
} else {
start = mid.add(BigInteger.valueOf(1));
}
}
if (res == null)
pw.println("Impossible");
else
pw.println(res);
pw.flush();
}
}
Java 中BigInteger类有几点需要注意:
1、所有算数运算都必须调用函数(Java中除了String重载了‘+’,其他不存在任何运算符重载)
2、BigInteger可视为final类,add()(加)、subtract()(减)、multiply()(乘)、divide()(除)等方法均不会改变两个操作数,而是返回一个新的对象。
3、无法表示的大数用字符串方法构造(new BigInteger(str)),原本是int/long类型的数现在要转化为BigInteger的,采用BigInteger.valueOf(val)方法构造。(该方法也会返回一个新的对象)
4、BigInteger类已实现toString()方法,默认返回该数在十进制下的字符串表示。因此可以直接把BigInteger类对象当做字符串输出。
5、BigInteger类的比较大小不能用=、<、>,而应该用compareTo()函数(返回值为一个int类型数据,为0代表相等,为正数代表前者大于后者,为负数则相反)。特别注意判断两个BigInteger相等不要自作聪明用.equals()方法(比如我 )
下面说C++怎么实现。
所有思路全部一样,只是有一点,C++不支持过大的整数。实际上也好办,我们就用long long来存储,如果运算结果过大导致溢出,这个数据就会变成负数。在由字符串转化为long long 时做一个判断,如果最终结果小于0,就把它看成是long long类型的最大值(9223372036854775807),反正它肯定不会符合最终结果,把这个值丢给二分查找,最后肯定是不相等。
#include 有人可能会说long long、int之类的最大值记不住。考试的时候用程序跑一下就行了。
int是231 -1,long long是264 -1。
这道题是PAT甲级题库里,第一道比较精彩的题目。