PAT甲级1010:Radix

Given a pair of positive integers, for example, 6 and 110, can this equation 6 = 110 be true? The answer is “yes”, if 6 is a decimal number and 110 is a binary number.

Now for any pair of positive integers N1 and N2, your task is to find the radix of one number while that of the other is given.

Input Specification:

Each input file contains one test case. Each case occupies a line which contains 4 positive integers:
N1 N2 tag radix
Here N1 and N2 each has no more than 10 digits. A digit is less than its radix and is chosen from the set {0-9, a-z} where 0-9 represent the decimal numbers 0-9, and a-z represent the decimal numbers 10-35. The last number “radix” is the radix of N1 if “tag” is 1, or of N2 if “tag” is 2.

Output Specification:

For each test case, print in one line the radix of the other number so that the equation N1 = N2 is true. If the equation is impossible, print “Impossible”. If the solution is not unique, output the smallest possible radix.

Sample Input 1:
6 110 1 10
Sample Output 1:
2
Sample Input 2:
1 ab 1 2
Sample Output 2:
Impossible

翻译:
给定一对正整数，例如6和110，这个等式6 = 110是否为真？答案是“是”，如果6是十进制数，110是二进制数的话。

现在对于任意一对正整数N1和N2，你的任务是找到一个数字的进制，而另一个数字的进制是给定的。

输入规格：

每个输入文件都包含一个测试样例。每个案例占据一个包含4个正整数的行：
N1 N2 tag radix
这里N1和N2每个都不超过10位。每个数字小于其进制，并且从集合{0-9，a-z}中选择，其中0-9表示十进制数字0-9，a-z表示十进制数字10-35。最后一个数字“radix”是“tag”为1时的N1的进制，如果“tag”为2则为N2的进制。

输出规格：

对于每个测试用例，在一行中打印另一个数字的进制，使得等式N1 = N2为真。如果方程式是不可能的，请打印“Impossible”。如果解决方案不是唯一的，则输出尽可能小的进制。

思路:虽然题目只给了0-9,a-z这36位数字,但最高进制并不是36,甚至要用unsigned long long
来表示. 因此不能顺序计算每一个进制. 事实上, 不同的进制下, 同一个数的大小不同, 并且这个数在较高进制下的大小始终不小于较低进制下的(在这里不说大于是因为只有一个数字下的特例,例如1在任何进制下都是1),因此可以使用二分查找来找到正确的进制.

注意:二分查找的下界是N2中最大数字(digit)加一,而上界是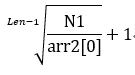 ,其中Len是N2数字(digit)位数且Len>1(Len=1的情况将首先讨论),N1此时用十进制表示,arr2[0]是N2的第一位数字.(用N1+1表示上界将会导致计算时一些数超出unsigned long long的范围).

(我的IDE为visual studio 2017)

#include "stdafx.h"
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

void CharToInt(char CharArray[], int IntArray[])//将字符串数组转换为int数组
{
    int Len = strlen(CharArray);
    for (int i = 0; i < Len; i++)
    {
        if (CharArray[i] >= '0'&&CharArray[i] <= '9')
        {
            IntArray[i] = CharArray[i] - '0';
            IntArray[10]++;
        }
        else if (CharArray[i] >= 'a'&&CharArray[i] <= 'z')
        {
            IntArray[i] = CharArray[i] - 'a' + 10;
            IntArray[10]++;
        }
    }
}
unsigned long long IntArrayToLong(int IntArray[], int NumOfArray, int Radix)//将数组中的各数字转换为数
{
    unsigned long long N = 0;
    for (int i = NumOfArray - 1; i >= 0; i--)
        N += IntArray[i] * pow(Radix, NumOfArray - 1 - i);
    return N;
}
int FindMax(int arr[],int N)//找到数组中最大元素
{
    int Max = 0;
    for (int i = 0; i < N; i++)
    {
        if (arr[i] > Max)
            Max = arr[i];
    }
    return Max;
}
int main()
{
    unsigned long long N1, N2;
    char str1[12], str2[12];
    int Tag, Radix;
    cin >> str1 >> str2 >> Tag >> Radix;//用字符串存储输入
    if (Tag == 2)
        swap(str1, str2);
    int arr1[11], arr2[11];
    CharToInt(str1, arr1);
    CharToInt(str2, arr2);
    N1 = IntArrayToLong(arr1, strlen(str1), Radix);//在十进制下表示N1
    if (strlen(str2) == 1)//处理N2只有一位数的情况
    {
        if (N1 > 35)
            cout << "Impossible" << endl;
        else
            cout << N1 + 1 << endl;
        return 0;
    }
    unsigned long long UpperBound = pow(1.0*N1 / arr2[0], 1.0 / (strlen(str2) - 1))+1;//上界
    unsigned LowerBound = FindMax(arr2, strlen(str2))+1;//下界
    for (; LowerBound <= UpperBound;)//二分查找
    {
        unsigned long long R = (LowerBound + UpperBound) / 2;
        N2 = IntArrayToLong(arr2, strlen(str2), R);
        if (N2 == N1)
        {
            cout << R << endl;
            return 0;
        }
        else if (LowerBound == UpperBound - 1)//处理下界比上界小一的情况,否则将陷入死循环
        {
            if (IntArrayToLong(arr2, strlen(str2), UpperBound-1) == N1)
            {
                cout << UpperBound-1 << endl;
                return 0;
            }
            if (IntArrayToLong(arr2, strlen(str2), UpperBound) == N1)
            {
                cout << UpperBound << endl;
                return 0;
            }
            break;
        }
        else if (N2 < N1)
            LowerBound=R;
        else if (N2 > N1)
            UpperBound = R;

    }
    cout << "Impossible" << endl;
    return 0;
}