Java数据结构与算法之单向循环链表
一、前言
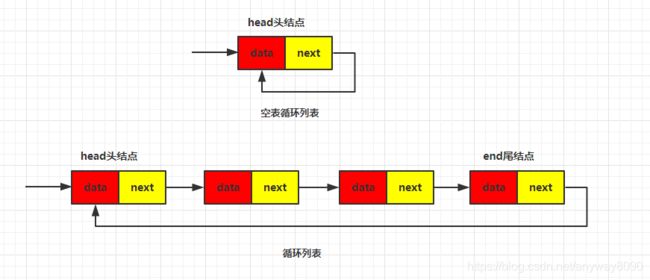
上篇内容中主要介绍了普通的单链表,这篇内容主要介绍下一种特殊的单链表——单向循环列表。下面先从图例中对单向循环链表有一个整体的概念。
从图例中可以看出,单向循环链表和普通的单链表区别主要在于尾结点,单链表的尾结点指向一个空的地址,从而表示这是最后的结点,而单向循环链表是将尾结点的指针指向了头结点,首尾相连。
二、单向循环列表的特点分析:
1、空表的循环列表是头结点的后继指针指向首结点自身 head.next=head;
2、循环列表中,尾结点后继指针指向了头结点 end.next=head
3、与单链表的区别还有一点,就是关于循环遍历链表时的判断条件,单链表的循环体的结束条件是p==null,而单向循环链表的循环判断条件是p.next==head,如下代码所示:
//单链表
Node p = this.head
while(p!=null){
}
//单向循环链表
Node p = this.head
while(p.next!=head){
} 除了判断添加的改变,其他实现方式是一样的。
3.1、首先先实现链表的存储单元,也就是结点类,结点类包括存储数据和后继指针两个元素
/**
* 结点类
* @author Administrator
*/
public class Node {
private E data;//存储数据
private Node next;
public Node(E data){
this.data=data;
}
public Node(E data,Node next){
this.data=data;
this.next=next;
}
} 3.2实现单向循环链表的顶级接口与单链表一致,包含链表的具体操作方法
package cn.cast.LinkedList;
/**
* 链表的顶级接口,包含所有
* 链表的基本方法
* @author Administrator
*
*/
public interface SingList {
//判断链表是否为空
boolean isEmpty();
//链表长度
int length();
//获取元素
T get(int index);
//根据index添加元素data
T set(int index,T data);
//根据index添加元素data
boolean add(T data);
//根据index插入元素
boolean add (int index,T data);
//删除指定位置的元素
T remove(int index);
//删除指定元素
boolean remove(T data);
//根据data移除所有相同元素
T removeAll(T data);
//清空链表
void clear();
//是否包含特定元素
boolean contains(T data);
//获取元素的位置
int indexOf(T data);
//根据data值查询最后一个出现在顺序表的下标
int lastIndexOf(T data);
// 输出格式
String toString();
}
3.3、实现顶级接口SingList
public class MySingList implements SingList{
private Node head;//头结点
private int length;//链表的长度
public MySingList(Node head){
this.head=head;
} 判断链表是否为空:由于链表的结构特点,头结点是链表的开始位置,所有判断链表是否为空,只要判断链表的头结点是为空
/**
* 判断链表是否为空
*/
@Override
public boolean isEmpty() {
return this.head==null;
}链表的长度大小:链表是存储的单元是结点,所有结点的数量也就是链表的长度。结点中存储着后继结点的引用地址,单向循环链表的终点是尾结点的指针为头结点,完成一个闭环,因此只需循环遍历所有结点,依次沿着后继指针循环,直到指针指向头结点,就可以得到链表的长度。
/**
* 获取链表的长度
*/
@Override
public int length() {
Node p=head;//将头结点赋值到临时变量p
if(p!=null){
while(p.next!=head){
p=p.next;//获取指向下一结点的指针
length++;//链表长度+1
}
}
return length;
} 获取元素:由于链表的结构特点,获取链表首先声明变量count(从0开始)来表示结点指向的位置,需要依次按照后继指针循环直到获取结点从而取得结点存储的数据。从程序来看,链表获取元素在最坏情况下需要依次遍历所结点,最好情况下时间复杂度为O(1),最坏情况下时间复杂度O(n)。而特别注意结点的结束判断,避免死循环。
/**
* 获取元素
*/
@Override
public T get(int index) {
if (head != null && index >= 0) {
int count = 0;// 用来元素的索引位置
Node p = this.head;// 存储结点的临时变量
// 获取对应的索引位置
while (p != null && count < index) {
p = p.next;
count++;
}
if (p.next != head) {
return p.data;
}
}
return null;
} 修改指定位置的元素:在获取元素位置时,与获取元素位置相同,修改元素只是在获取元素后用新的存储数据替换旧的存储数据data。在时间复杂度上,与获取元素相同。
/**
*修改元素
*/
@Override
public T set(int index, T data) {
if (head != null && index >= 0) {
int count = 0;// 用来元素的索引位置
Node p = this.head;// 存储结点的临时变量
// 获取对应的索引位置
while (p != null && count < index) {
p = p.next;
count++;
}
//获取需要替换的存储数据,用新的存储数据替换旧的存储数据,返回旧值
if(p.next!=head){
T oldData=p.data;
p.data=data;
return oldData;
}
}
return null;
} 添加元素:单链表添加元素主要分为四种场景,a.空链表插入结点;b.头结点插入元素,新增结点为头结点;c.中间情况插入节点;d.尾结点插入元素,也就是在插入在单链表末尾,下面从流程图分析下四种场景 。
下面具体来分析下四种具体情况:
a.插入空链表:此时链表为空,插入结点即为空结点
if(head==null){
head=new Node(datal);
head.next=head;//头结点指向自身
} b.头结点前插入元素:新插入结点即为新头结点,插入结点的指针指向原头结点
if(index==0 && head!=null){
Node node =new Node(data);//新结点实例
node.next=head;//将新结点的后继指针指向原头结点
head=node;//新结点赋值为头结点
} c.中间结点插入元素:在链表中间位置插入新元素,首先获取插入位置的前一个结点,将插入位置的索引向前移动,将新插入元素的后继指针指向原插入位置的结点。
if(index>0 && head!=null && index p = this.head;// 存储结点的临时变量
// 获取对应的索引位置
while (p != null && scanIndex < index-1) {
p = p.next;//将索引向前移
scanIndex++;
}
Node node =new Node(data);
node.next=p.next;//新结点后继指针指向原结点的后继结点
p.next=node;
} d.链表末尾插入元素:在链表末尾插入结点,即新插入结点为新的尾结点,同时,尾结点后继指针指向head。
if(index>0 && head!=null && index=length()){
int scanIndex = 0;// 扫描索引
Node p = this.head;// 存储结点的临时变量
// 获取对应的索引位置
while (p != null && scanIndex < index-1) {
p = p.next;//将索引向前移
scanIndex++;
}
Node node =new Node(data);
node.next=p.next;//新结点后继指针指向原结点的后继结点
p.next=node;
return true;
} 在末尾和中间插入代码可以合并,最终代码如下:
@Override
public boolean add(int index, T data) {
if(head==null){
head=new Node(data);
head.next=head
return true;
}
if(index==0 && head!=null){
Node node =new Node(data);
node.next=head;
head=node;
return true;
}
if(index>0 && head!=null && index<=length()){
int scanIndex = 0;// 扫描索引
Node p = this.head;// 存储结点的临时变量
// 获取对应的索引位置
while (p != null && scanIndex < index-1) {
p = p.next;//将索引向前移
scanIndex++;
}
Node node =new Node(data);
node.next=p.next;//新结点后继指针指向原结点的后继结点
p.next=node;
return true;
}
return false;
} 在尾部插入结点:
@Override
public boolean add(T data) {
return this.add(length(),data);
}删除指定位置的元素:删除元素与插入结点类型,首先要先找到要删除指定位置的索引位置分为三种情况,删除头结点,删除中间位置结点,删除尾结点;
@Override
public T remove(int index) {
// 链表尾空
if (isEmpty()) {
return null;
}
// 删除头结点
if (index == 0) {
Node oldHead = head;
head = head.next;
return oldHead.data;
}
// 删除中间结点
if (index != 0 && index <= length()) {
int scanIndex = 0;// 扫描索引
Node p = this.head;// 存储结点的临时变量
// 找到目标结点的前一个结点
while (p != null && scanIndex < index - 1) {
p = p.next;// 将索引向前移
scanIndex++;
}
Node targetNode = p.next;// 目标结点
if (targetNode != null) {
T oldData = targetNode.data;
p.next = targetNode.next;
targetNode = null;// 将目标结点置为null,切断关联关系
return oldData;
}
}
return null;
} 其他方法:
//清空链表
@Override
public void clear() {
this.head.=null;
}
//判断链表是否含有某元素结点
@Override
public boolean contains(T data) {
//数据合法性校验
if(data==null){
return false;
}
//链表为空时
if(isEmpty()){
return false;
}
//依据后继指针循环链表
Node p = head;
while(p.next!=head){
T nodeData= p.data;
if(data.equals(nodeData)){
return true;
}
p=p.next;
}
return false;
} 总结:单向循环链表与普通链表的区别主要是在尾结点的判断,查询的时间复杂度都为O(1),插入和删除的时间复杂度为O(n),