数据结构 -- 并查集
时间过得真快,一眨眼集训第二周就要结束了。有很长的第一段时间没有写算法类的博客了。今天先来一篇 --- 并查集。
1、什么是并查集
并查集(Union Find)是一种用于管理分组的数据结构。它具备两个操作:(1)查询元素a和元素b是否为同一组 (2) 将元素a和b合并为同一组。
注意:并查集不能将在同一组的元素拆分为两组。
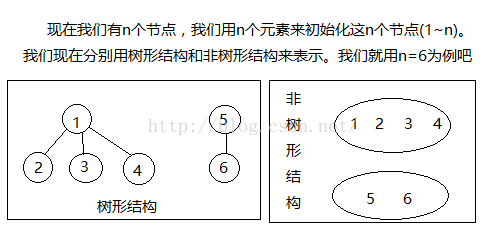
2、并查集的结构
并查集可以使用树来实现。
使用树形结构来表示以后,每一组都对应一棵树,然而我们就可以将这个问题转化为树的问题了,我们看两个元素是否为一组我们只要看这两个元素的根是否一致。显然,使用树形结构将问题简单化了。合并时是我们只需要将一组的根与另一组的根相连即可。
3、并查集的实现
我们通过以上的思路,现在就可以具体来实现并查集了,代码如下:
int node[i]; //每个节点
//初始化n个节点
void Init(int n){
for(int i = 0; i < n; i++){
node[i] = i;
}
}
//查找当前元素所在树的根节点(代表元素)
int find(int x){
if(x == node[x])
return x;
return find(node[x]);
}
//合并元素x, y所处的集合
void Unite(int x, int y){
//查找到x,y的根节点
x = find(x);
y = find(y);
if(x == y)
return ;
//将x的根节点与y的根节点相连
node[x] = y;
}
//判断x,y是属于同一个集合
bool same(int x, int y){
return find(x) == find(y);
}有了这些知识,我们就可以来解决一些问题了。先上两道并查集的水题:畅通工程,How many Tables?
4、并查集的优化
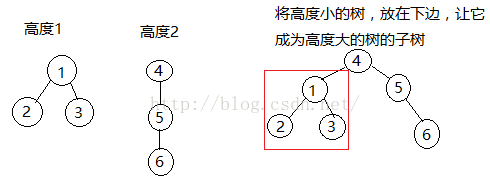
细心的同学会发现,我们使用以上的代码来实现并查集,会出现一个问题 --- 树的退化。在树形数据结构中,如果发生退化,那么复杂度将会变得很高(最惨的是直接退化成线性结构)。因此我们必须设法,阻止这种退化。为此我们这里有两种方法。
<1>对于每一棵树,我们记录它的高度(rank)。在每次合并操作时,将高度小的树 放在 高度高的树下,成为它的子树:
通过这样处理之后,可以有效的防止树的退化,但是查询效率还不够快,于是我们有提出了第二种优化方案。
<2>路径压缩
我们将原先间接与根相连的节点,让它与根直连,这样效率又可以大大的提高了:
我们在第一次查询时,进行这步操作,当再次查询时,就大大提高了效率。
5、并查集的复杂度
加入这两个优化之后,并查集的效率就非常高。对n个元素的并查集操作一次的复杂度是: O(α(n))。这里,α(n)是阿克曼(Ackermann)函数的反函数。效率要高于O(log n)。
不过这里O(α(n))是平均复杂度。也就是说,多次操作之后平均复杂度为O(α(n)),换而言之,并不是每一次操作都满足O(α(n))。
6、优化后的并查集实现
int node[i]; //每个节点
int rank[i]; //树的高度
//初始化n个节点
void Init(int n){
for(int i = 0; i < n; i++){
node[i] = i;
rank[i] = 0;
}
}
//查找当前元素所在树的根节点(代表元素)
int find(int x){
if(x == node[x])
return x;
return node[x] = find(node[x]); //在第一次查找时,将节点直连到根节点
}
//合并元素x, y所处的集合
void Unite(int x, int y){
//查找到x,y的根节点
x = find(x);
y = find(y);
if(x == y)
return ;
//判断两棵树的高度,然后在决定谁为子树
if(rank[x] < rank[y]){
node[x] = y;
}else{
node[y] = x;
if(rank[x] == rank[y]) rank[x]++:
}
}
//判断x,y是属于同一个集合
bool same(int x, int y){
return find(x) == find(y);
} 现在我们已经大致的来解了并查集,我们来一道,有一点难度的题目练练手:食物链