数据结构与算法分析:(四)双向链表
一、双向链表介绍
我们上一篇主要介绍了关于单向链表的操作,数据结构与算法分析:(三)单向链表。
我们先来介绍下单向链表与双向链表的一些差异:
1、单向链表
- 只能从头遍历到尾或者从尾遍历到头(一般从头到尾)。
- 链表相连的过程是单向的,实现的原理是上一个链表中有一个指向下一个链表的引用。
- 缺点:
a、单向链表不能自我删除,需要先找到被删除节点的前一个节点front,使用front节点来辅助删除,不方便。
b、可轻松的到达下一个节点, 但是回到前一个节点是很难的。
2、双向链表
- 既可以从头遍历到尾, 又可以从尾遍历到头。
- 链表相连的过程是双向的。一个节点既有向前连接的引用,也有一个向后连接的引用。
- 双向链表可以有效的解决单向链表中提到的问题。
- 缺点:
a、每次在插入或删除某个节点时,需要处理四个节点的引用,而不是两个。实现起来困难一些。
b、相对于单向链表,必然占用内存空间更大一些。
3、 双向链表的图解: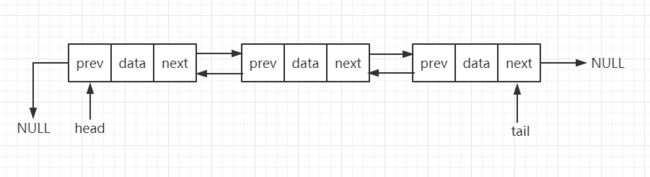
从我画的图中可以看出来,双向链表需要额外的两个空间来存储后继结点和前驱结点的地址。所以,如果存储同样多的数据,双向链表要比单链表占用更多的内存空间。虽然两个指针比较浪费存储空间,但可以支持双向遍历,这样也带来了双向链表操作的灵活性。那相比单链表,双向链表适合解决哪种问题呢?
从结构上来看,双向链表可以支持 O(1) 时间复杂度的情况下找到前驱结点,正是这样的特点,也使双向链表在某些情况下的插入、删除等操作都要比单链表简单、高效。
我们接下来就不像上一篇那样详细的画图然后贴代码说明了。我们这里重点来介绍删除与插入操作。
二、双向链表的删除与插入操作
在实际的软件开发中,从链表中删除一个数据无外乎这两种情况:
- 删除结点中“值等于某个给定值”的结点;
- 删除给定指针指向的结点。
对于第一种情况,不管是单链表还是双向链表,为了查找到值等于给定值的结点,都需要从头结点开始一个一个依次遍历对比,直到找到值等于给定值的结点,然后再通过我前面讲的指针操作将其删除。
尽管单纯的删除操作时间复杂度是 O(1),但遍历查找的时间是主要的耗时点,对应的时间复杂度为 O(n)。根据时间复杂度分析中的加法法则,删除值等于给定值的结点对应的链表操作的总时间复杂度为 O(n)。
对于第二种情况,我们已经找到了要删除的结点,但是删除某个结点 q 需要知道其前驱结点,而单链表并不支持直接获取前驱结点,所以,为了找到前驱结点,我们还是要从头结点开始遍历链表,直到 p->next=q,说明 p 是 q 的前驱结点。
但是对于双向链表来说,这种情况就比较有优势了。因为双向链表中的结点已经保存了前驱结点的指针,不需要像单链表那样遍历。所以,针对第二种情况,单链表删除操作需要 O(n) 的时间复杂度,而双向链表只需要在 O(1) 的时间复杂度内就搞定了!
同理,如果我们希望在链表的某个指定结点前面插入一个结点,双向链表比单链表有很大的优势。双向链表可以在 O(1) 时间复杂度搞定,而单向链表需要 O(n) 的时间复杂度。
除了插入、删除操作有优势之外,对于一个有序链表,双向链表的按值查询的效率也要比单链表高一些。因为,我们可以记录上次查找的位置 p,每次查询时,根据要查找的值与 p 的大小关系,决定是往前还是往后查找,所以平均只需要查找一半的数据。
现在,你有没有觉得双向链表要比单链表更加高效呢?这就是为什么在实际的软件开发中,双向链表尽管比较费内存,但还是比单链表的应用更加广泛的原因。如果你熟悉 Java 语言,你肯定用过 LinkedHashMap、LinkedList这个容器。如果你深入研究 LinkedHashMap 的实现原理,就会发现其中就用到了双向链表这种数据结构。
实际上,这里有一个更加重要的知识点需要你掌握,那就是用空间换时间的设计思想。当内存空间充足的时候,如果我们更加追求代码的执行速度,我们就可以选择空间复杂度相对较高、但时间复杂度相对很低的算法或者数据结构。相反,如果内存比较紧缺,比如代码跑在手机或者单片机上,这个时候,就要反过来用时间换空间的设计思路。
缓存实际上就是利用了空间换时间的设计思想。如果我们把数据存储在硬盘上,会比较节省内存,但每次查找数据都要询问一次硬盘,会比较慢。但如果我们通过缓存技术,事先将数据加载在内存中,虽然会比较耗费内存空间,但是每次数据查询的速度就大大提高了。
总结一下,对于执行较慢的程序,可以通过消耗更多的内存(空间换时间)来进行优化;而消耗过多内存的程序,可以通过消耗更多的时间(时间换空间)来降低内存的消耗。
三、双向链表的代码实现
1、.因为链表由一个一个的节点组成,因此需要定义一个节点类(Node)。假设属性包括id、name(这些是节点的数据域),和prev、next(指针域)。
Node类
public class Node {
private int id;
private String name;
private Node prev, next;// 前驱与后驱结点
public int getId() {
return id;
}
public void setId(int id) {
this.id = id;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public Node getPrev() {
return prev;
}
public void setPrev(Node prev) {
this.prev = prev;
}
public Node getNext() {
return next;
}
public void setNext(Node next) {
this.next = next;
}
}
2、定义一个DubboLinkedList 双向链表类,DubboLinkedList 类包括一个成员变量head,是链表的头结点。
DubboLinkedList 类
/**
* 双向链表
*/
public class DubboLinkedList {
// 头结点,头结点不保存数据
Node head = new Node();
// 获取链表的第一个节点(不是头结点)
public Node getFirst() {
return head.getNext();
}
// 获取链表的最后那个节点
public Node getLast() {
// temp变量来保存链表的最后那个节点
Node temp = head;
while (temp.getNext() != null) {
temp = temp.getNext();
}
// 循环结束时,temp就是最后那个节点
return temp;
}
// 根据id查找指定节点
public Node get(int id) {
Node temp = head.getNext();
while (temp != null) {
if (temp.getId() == id) {
break;
}
// temp后移
temp = temp.getNext();
}
return temp;
}
// 正序遍历链表
public void list() {
// 判空
if (head.getNext() == null) {
System.out.println("DubboLinkedList is empty");
return;
}
Node temp = head.getNext();
while (temp != null) {
System.out.println(temp);
// temp后移
temp = temp.getNext();
}
}
// 倒序遍历链表
public void reverseOrderList() {
// 判空
if (head.getNext() == null) {
System.out.println("DubboLinkedList is empty");
return;
}
// 先得到最后那个节点
Node temp = getLast();
while (temp != null) {
System.out.println(temp);
temp = temp.getPrev();
if (temp.getPrev() == null) {
// 如果temp.getPrev()==null,说明当前temp是头结点,不打印头结点
break;
}
}
}
// 添加新节点到链表尾部
public void append(Node node) {
Node last = getLast();
// 添加新节点
last.setNext(node);
node.setPrev(last);
}
// 插入节点到指定节点后
public void insertAfter(Node node, Node newNode) {
// 先根据id找到这个节点
Node beforeNode = get(node.getId());
// 插入节点
beforeNode.getNext().setPrev(newNode);
newNode.setNext(beforeNode.getNext());
beforeNode.setNext(newNode);
newNode.setPrev(beforeNode);
}
// 删除指定节点,并返回被删除节点
public Node delete(Node node) {
if (head.getNext() == null) {
System.out.println("DubboLinkedList is empty");
return null;
}
// 找到被删除节点
Node deleteNode = get(node.getId());
if (deleteNode == null) {
System.out.println("The specified node was not found");
return deleteNode;
}
// 删除节点
deleteNode.getPrev().setNext(deleteNode.getNext());
// 如果被删除的节点不是最后那个节点才执行,因为最后的节点的next指针为null,不判断可能产生空指针异常
if (deleteNode.getNext() != null) {
deleteNode.getNext().setPrev(deleteNode.getPrev());
}
return deleteNode;
}
// 修改节点
public boolean update(Node node) {
// 先找到节点
Node updateNode = get(node.getId());
if (updateNode == null) {
return false;
}
updateNode.setName(node.getName());
return true;
}
}
四、思考:如何基于链表实现 LRU 缓存淘汰算法?
我的思路是这样的:我们维护一个有序链表,越靠近链表尾部的结点是越早之前访问的。当有一个新的数据被访问时,我们从链表头开始顺序遍历链表。
1、如果此数据之前已经被缓存在链表中了,我们遍历得到这个数据对应的结点,并将其从原来的位置删除,然后再插入到链表的头部。
2、如果此数据没有在缓存链表中,又可以分为两种情况:
- 如果此时缓存未满,则将此结点直接插入到链表的头部;
- 如果此时缓存已满,则链表尾结点删除,将新的数据结点插入链表的头部。
Talk is cheap, show me the code.
import java.util.HashMap;
import java.util.Map;
public class LRUCache {
public static class DoublyLinkedList {
DoublyLinkedList prev, next;
Integer key, value;
}
DoublyLinkedList head, tail;
Integer capacity;
Map<Integer, DoublyLinkedList> map = new HashMap<Integer, DoublyLinkedList>();
public LRUCache(int capacity) {
this.capacity = capacity;
head = new DoublyLinkedList();
tail = new DoublyLinkedList();
head.next = tail;
tail.prev = head;
}
private void put(int key, int value) {
DoublyLinkedList node = map.get(key);
if (node == null) {
capacity--;
node = new DoublyLinkedList();
node.key = key;
node.value = value;
map.put(key, node);
moveToHead(node);
if (capacity < 0) {
DoublyLinkedList temp = removeTailnode();
map.remove(temp.key);
capacity++;
}
} else {
node.value = value;
map.put(key, node);
moveToHead(node);
}
}
private Integer get(int key) {
DoublyLinkedList node = map.get(key);
remove(node);
moveToHead(node);
return node.value;
}
private void moveToHead(DoublyLinkedList node) {
node.prev = head;
node.next = head.next;
head.next = node;
node.next.prev = node;
}
private DoublyLinkedList removeTailnode() {
DoublyLinkedList temp = tail.prev;
remove(temp);
return temp;
}
private void remove(DoublyLinkedList temp) {
DoublyLinkedList p = temp.prev;
DoublyLinkedList q = temp.next;
p.next = q;
q.prev = p;
}
}
下面这篇文章还有两种不同的实现方式,可参考:用java自己实现一个LRU