数据结构-堆

定义

优先队列：一种特殊的队列，队列中元素出栈的顺序是按照元素的优先权大小，而不是元素入队的先后顺序。

堆的特性：

• 必须是完全二叉树
• 用数组实现
• 任一结点的值是其子树所有结点的最大值或最小值
  
  • 最大值时，称为“最大堆”，也称大顶堆；
  • 最小值时，称为“最小堆”，也称小顶堆。

可以看到，对于堆（Heap）这种数据结构，从根节点到任意结点路径上所有的结点都是有序的。

堆的ADT

堆的实现

堆是用数组实现的完全二叉树，因此在Java中我们可以使用ArrayList实现，而且向ArrayList中插入元素时，当数组容量不足时，他会自动增长，这样也免去考虑堆最大容量的问题。这里重点描述以上ADT中插入和删除的操作。一般来说，会从堆中删除最大值，其实也就是最大堆中的第一个元素。下面的实现为了普适性，实现了从堆中删除任一结点的操作。

下面就以最大堆的构成为例，研究一下如何使用数组实现堆。

最大堆

插入

堆的插入如何实现呢？只要我们谨记堆的定义，实现起来其实是很容易的。这里在回顾一下重点

1. 完全二叉树
2. 任一结点的值是其左右子树的最大值
3. 用数组实现

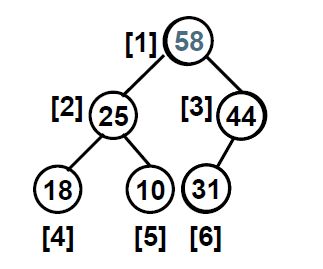
考虑下图所示的堆。

假设现有元素60需要插入，为了维持完全二叉树的特性，新插入的元素一定是放在结点44的右子树；同时为了满足任一结点的值要大于左右子树的值这一特性，新插入的元素要和其父结点作比较，如果比父结点大，就要把父结点拉下来顶替当前结点的位置，自己则依次不断向上寻找，找到比自己小的父结点就拉下来，直到没有符合条件的值为止。这样，到最后就完成了插入操作；总结一下：

1. 新插入的结点添加到数组最后
2. 和其父结点比较大小，如果大于父结点，就用父结点替换当前位置，同时自己的位置上移。
3. 直到父结点不再大于自己或者是位置已近到了数组第一个位置，就找到属于自己的位置了。

这里为了方便，我们直接占用了数组下标为0的位置，在0的位置放置了一个null，这样数组中实际有效值的下标就和我们完全二叉树中层序遍历的实际序号对应了。这样，完全二叉树中，如果结点值为n,那么其左子树则为2n,右子树为2n+1；换句话说，对于任一结点n,其父结点为n/2 取整即可。

• 初始化堆

public class MaxHeap<T extends Comparable<T>> {

    private List mHeap;

    public MaxHeap() {
        mHeap = new ArrayList<>();
        // 为了方便，数组下标为0 的位置，放置一个空元素，使得数组从下标为1的位置开始
        // 这样，完全二叉树中，如果结点值为n,那么其左子树则为2n,右子树为2n+1
        mHeap.add(0, null);
    }

}

当然，为了保证有序性，我们需要堆内元素实现了Comparable接口。

• 插入操作

/**
     * 堆的插入操作
     * @param value
     */
    public void insert(T value) {
        //新插入的元素首先放在数组最后，保持完全二叉树的特性
        mHeap.add(value);
        // 获取最后一个元素的在数组中的索引位置,注意是从index=1的位置开始添加
        int index = mHeap.size() - 1;
        // 其父结点位置
        int pIndex = index / 2;



        //在数组范围内，比较这个插入值和其父结点的大小关系，大于父结点则用父结点替换当前值，index位置上升为父结点
        while (index > 1) {
            // 插入结点小于等于其父结点，则不用调整
            if (compare(value, mHeap.get(pIndex)) <= 0) {
                break;
            } else {
                // 依次把父结点较小的值“将”下来
                mHeap.set(index, mHeap.get(pIndex));
                // 向上升一层
                index = pIndex;
                // 新的父结点
                pIndex = index / 2;
            }
        }
        // 最终找到index 的位置，把值放进去
        mHeap.set(index, value);


    }

    /**
     *  
     * @param a
     * @param b
     * @return a>b 返回值大于0，反之小于0
     */
    private int compare(T a, T b) {
        return a.compareTo(b);
    }

这里需要注意的是，当插入结点大于父结点时，我们并没有交换两个元素的算法，而只是把小的元素“降”了下来，因为我们最终只是想要找到一个正确的位置而已，交换是不必要，只需要在最后在合适的位置把值放上去就可以了。

删除

理解了插入的实现，删除也是遵循同样的规则。

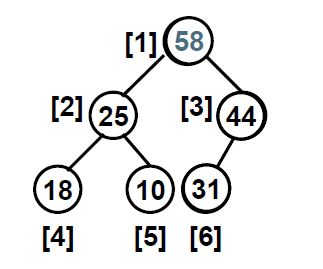
假设要从上图中删除结点58，为了维持完全二叉树的特性，我们很容易想到用最后一个元素31去替代这个58；然后比较31和其子树的大小关系，如果比左右子树小（如果存在的话），就要从左右子树中找一个较大的值替换他，而他能自己就要跑到对应子树的位置，再次循环这种操作，直到没有子树比他小就可以了。在这里，按照以上的思路，44将跑到根节点的位置，而他的位置将由31替代，堆依然是堆。总结一下：

1. 找到要删除的结点在数组中的位置
2. 用数组中最后一个元素替代这个位置的元素
3. 当前位置和其左右子树比较，保证符合最大堆的结点间规则
4. 删除最后一个元素

/**
     * 堆的任意值的删除操作
     * @param value
     * @return
     */
    public boolean delete(T value) {
        if (mHeap.isEmpty()) {
            return false;
        }
        // 得到数组中这个元素的下标
        int index = mHeap.indexOf(value);
        if (index == -1) { // 被删除元素不在数组中，即删除元素不在堆中
            return false;
        }

        // 获取最后一个元素的在数组中的索引位置,注意是从index=1的位置开始添加
        int lastIndex = mHeap.size() - 1;

        T temp = mHeap.get(lastIndex);
        // 用最后一个元素替换被删除的位置
        mHeap.set(index, temp);


        int parent;
        for (parent = index; parent * 2 <= mHeap.size()-1; parent = index) {
            //当前结点左子树下标
            index = parent * 2;
            // 左子树下标不等于数组长度，因此必然有右子树 ,则左右子树比较大小，这里-1 是因为数组下标=1 开始
            if (index != mHeap.size()-1 && compare(mHeap.get(index), mHeap.get(index + 1))<0) {
                // 如果右子树大，则下标指向右子树
                index=index+1;
            }

            if (compare(temp, mHeap.get(index)) > 0) {
                //当前结点大于其左右子树，则不用调整，直接退出
                break;
            }else {
                // 子树上移，替换当前结点
                mHeap.set(parent, mHeap.get(index));
            }


        }
        // parent 就是替换结点最终该处的位置
        mHeap.set(parent, temp);
        // 移除数组最后一个元素
        mHeap.remove(lastIndex);
        return true;


    }

关于删除操作，需要注意的一点就是，由于我们的数组相当于是从下标=1 的位置开始，因此需要注意数组边界值和其长度的关系。

下面就来测试一下最大堆的实现：

测试类

    private static Integer[] arrays = new Integer[]{10, 8, 3, 12, 9, 4, 5, 7, 1, 11, 17};

    private static void MaxHeapTest() {
        MaxHeap mMaxHeap = new MaxHeap<>();
        for (int i = 0; i < arrays.length; i++) {
            mMaxHeap.insert(arrays[i]);
        }

        mMaxHeap.printHeap();
        System.out.printf("delete value %d from maxHeap isSuccess=%b \n", 17, mMaxHeap.delete(17));
        mMaxHeap.printHeap();
        System.out.printf("delete value %d from maxHeap isSuccess=%b \n", 1, mMaxHeap.delete(1));
        mMaxHeap.printHeap();
        System.out.printf("delete value %d from maxHeap isSuccess=%b \n", 12, mMaxHeap.delete(12));
        mMaxHeap.printHeap();
        System.out.printf("insert value %d to maxHeap \n", 16);
        mMaxHeap.insert(16);
        mMaxHeap.printHeap();

    }

printHeap() 的实现可以参考以下最小堆完整源码。

输出：

17 12 5 8 11 3 4 7 1 9 10 
delete value 17 from maxHeap isSuccess=true 
12 11 5 8 10 3 4 7 1 9 
delete value 1 from maxHeap isSuccess=true 
12 11 5 8 10 3 4 7 9 
delete value 12 from maxHeap isSuccess=true 
11 10 5 8 9 3 4 7 
insert value 16 to maxHeap 
16 11 5 10 9 3 4 7 8 

可以看到，当我们第一次完成遍历插入后，将构建出如下所示的一颗完全二叉树，很显然这也是最大堆。当我们一次删除元素或插入元素时，根据输出结果对应的堆，可以看到我们的插入和删除操作都是正确的。

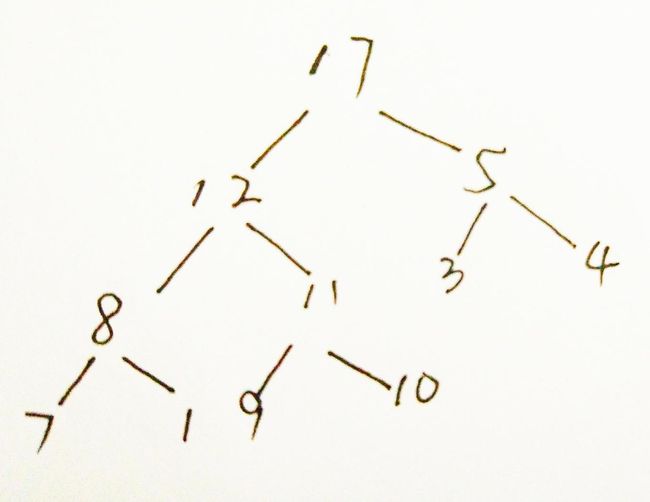
这棵树画歪了，凑合看吧，o(╯□╰)o。

后面几个输出对应的树，感兴趣的同学可以手动画一下，学二叉树手动画树真是一个好方法。

最小堆

最小堆，每一个结点的值都小于其左右子树的值，因此很容易的我们可以想到，在构建最大树时把所有判断大小的逻辑取反就可以实现了。事实上也的确就是这么简单，下面给出完整最小堆实现的完整代码，就不具体分析了。

public class MinHeap<T extends Comparable<T>> {
    private List mHeap;
    //堆内当前元素个数
    public int size;

    public MinHeap() {
        mHeap = new ArrayList<>();
        // 为了方便，数组下标为0 的位置，放置一个空元素，使得数组从下标为1的位置开始
        // 这样，完全二叉树中，如果结点值为n,那么其左子树则为2n,右子树为2n+1
        mHeap.add(0, null);
    }

    public void insert(T value) {
        //新插入的元素首先放在数组最后，保持完全二叉树的特性
        mHeap.add(value);
        // 获取最后一个元素的在数组中的索引位置,注意是从index=1的位置开始添加，因此最后一个元素的位置是size-1
        int index = mHeap.size() - 1;
        // 其父结点位置
        int pIndex = index / 2;



        //在数组范围内，比较这个插入值和其父结点的大小关系，小于父结点则用父结点替换当前值，index位置上升为父结点
        while (index > 1) {
            // 插入结点大于等于其父结点，则不用调整
            if (compare(value, mHeap.get(pIndex)) >= 0) {
                break;
            } else {
                // 依次把父结点较大的值“将”下来,把小的值升上去
                mHeap.set(index, mHeap.get(pIndex));
                // 向上升一层
                index = pIndex;
                // 新的父结点
                pIndex = index / 2;
            }
        }
        // 最终找到index 的位置，把值放进去
        mHeap.set(index, value);


    }


    public boolean remove(T value) {
        if (mHeap.isEmpty()) {
            return false;
        }
        // 得到数组中这个元素的下标
        int index = mHeap.indexOf(value);
        if (index == -1) { // 被删除元素不在数组中，即删除元素不在堆中
            return false;
        }

        // 获取最后一个元素的在数组中的索引位置,注意是从index=1的位置开始添加，因此最后一个元素的位置是size-1
        int lastIndex = mHeap.size() - 1;

        T temp = mHeap.get(lastIndex);
        // 用最后一个元素替换被删除的位置
        mHeap.set(index, temp);


        int parent;
        for (parent = index; parent * 2 <= mHeap.size()-1; parent = index) {
            //当前结点左子树下标
            index = parent * 2;
            // 左子树下标不等于数组长度，因此必然有右子树 ,则左右子树比较大小
            if (index != mHeap.size()-1 && compare(mHeap.get(index), mHeap.get(index + 1))>0) {
                // 如果右子树小，则下标指向右子树
                index=index+1;
            }

            if (compare(temp, mHeap.get(index)) < 0) {
                //当前结点小于其左右子树，则不用调整，直接退出
                break;
            }else {
                // 子树上移，替换当前结点
                mHeap.set(parent, mHeap.get(index));
            }


        }
        // parent 就是替换结点最终该处的位置
        mHeap.set(parent, temp);
        // 移除数组最后一个元素
        mHeap.remove(lastIndex);
        return true;


    }

    private int compare(T a, T b) {
        return a.compareTo(b);
    }

    public void printHeap(){
        StringBuilder sb = new StringBuilder();
        for(int i=1;i" ");
        }

        System.out.println(sb.toString());
    }
}

测试类就不在这里占篇幅了，有兴趣的同学可以直接看源码.

---

好了，堆的实现就到这里了。