LeetCode-912、排序数组-中等
LeetCode-912、排序数组-中等
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1]
输出:[1,2,3,5]
示例 2:
输入:nums = [5,1,1,2,0,0]
输出:[0,0,1,1,2,5]
提示:
1 <= nums.length <= 50000
-50000 <= nums[i] <= 50000
代码:
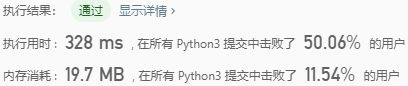
1、快速排序:使用分治法(Divide and conquer)策略。挑选基准值,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面,递归地将小于基准值元素的子序列和大于基准值元素的子序列排序。递归到最底部的判断条件是数列的大小是零或一,此时该数列显然已经有序。选取基准值有数种具体方法,此选取方法对排序的时间性能有决定性影响。
时间复杂度:O(Nlog2(N))
class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
def partition(n, left, right):
tmp = n[right]
ind = left
for i in range(left, right):
if n[i] < tmp:
n[ind], n[i] = n[i], n[ind]
ind += 1
n[ind], n[right] = n[right], n[ind]
return ind
def quicksort(n, left, right):
if left < right:
ind = partition(n, left, right)
quicksort(n, left, ind-1)
quicksort(n, ind+1, right)
quicksort(nums, 0, len(nums)-1)
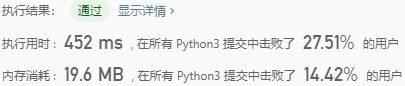
return nums2、归并排序:创建在归并操作上的一种有效的排序算法,是采用分治法(Divide and Conquer)的一个非常典型的应用。
时间复杂度:O(Nlog2(N))
class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
def merge(n, l, m, r):
alen = m + 1 - l
blen = r - m
a = [0] * alen
b = [0] * blen
for i in range(l, m+1):
a[i-l] = n[i]
for i in range(m+1, r+1):
b[i-m-1] = n[i]
i, j, k = 0, 0, l
while i < alen and j < blen:
if a[i] < b[j]:
n[k] = a[i]
i += 1
else:
n[k] = b[j]
j += 1
k += 1
while i < alen:
n[k] = a[i]
i += 1
k += 1
while j < blen:
n[k] = b[j]
j += 1
k += 1
def mergesort(n, l, r):
if l < r:
m = (l + r) // 2
mergesort(n, l, m)
mergesort(n, m+1, r)
merge(n, l, m, r)
mergesort(nums, 0, len(nums)-1)
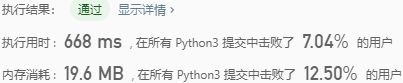
return nums3、堆排序:利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。N元素数组,从最后一个节点向根节点建大顶堆,每次交换父节点和子节点的值后都要重新堆化所有子节点,找到最大值后将根节点与最后一个子节点交换,再对前(N-1)个元素重新堆化。
时间复杂度:O(Nlog2(N))
class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
def heapify(n, end, i):
tmpmaxind = i
l = 2 * i + 1
r = 2 * i + 2
if l < end and n[tmpmaxind] < n[l]:
tmpmaxind = l
if r < end and n[tmpmaxind] < n[r]:
tmpmaxind = r
if tmpmaxind != i:
n[i], n[tmpmaxind] = n[tmpmaxind], n[i]
heapify(n, end, tmpmaxind)
def heapSort(n):
end = len(n)
for i in range(end-1, -1, -1):
heapify(n, end, i)
for i in range(end-1, 0, -1):
n[0], n[i] = n[i], n[0]
heapify(n, i, 0)
heapSort(nums)
return nums4、插入排序:通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。递归地把当前序列平均分割成两半,在保持元素顺序的同时将上一步得到的子序列集成到一起(归并)。
时间复杂度:O(N^2)
class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
def insertionsort(n):
for i in range(len(n)):
tmp = n[i]
j = i -1
while j >= 0 and n[j] > tmp:
n[j+1] = n[j]
j -= 1
n[j+1] = tmp
insertionsort(nums)
return nums
常见排序方法复杂度:
| 排序方法 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 | 复杂性 |
| 直接插入排序 | O(n^2) | O(n^2) | O(n) | O(1) | 稳定 | 简单 |
| 希尔排序 | O(nlog2n) | O(n^2) | O(n^1.3) | O(1) | 不稳定 | 较复杂 |
| 直接选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 | 简单 |
| 堆排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(1) | 不稳定 | 较复杂 |
| 冒泡排序 | O(n^2) | O(n^2) | O(n) | O(1) | 稳定 |
简单 |
| 快速排序 | O(nlog2n) | O(n^2) | O(nlog2n) | O(nlog2n) | 不稳定 | 较复杂 |
| 归并排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(n) | 稳定 |
较复杂 |
| 基数排序 | O(d(n+r)) | O(d(n+r)) | O(d(n+r)) | O(n+r) | 稳定 |
较复杂 |