Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines 论文研读
摘要
本文提出了一种用于训练支持向量机的新算法:序列最小优化算法(SMO)。训练支持向量机需要解决非常大的二次规划(QP)优化问题。SMO 将这个大的 QP 问题分解为一系列最小的 QP 问题。这些小的 QP 问题可以通过解析来解决,从而避免了将耗时的数值 QP 优化用作内部循环。SMO 所需的内存量与训练集大小成线性关系,这使 SMO 可以处理非常大的训练集。由于避免了矩阵计算,因此对于各种测试问题,SMO 随训练集大小在线性和二次方之间缩放,而标准分块 SVM 算法随训练集大小在线性和三次方之间缩放。SMO 的计算时间主要由 SVM 评估决定,因此 SMO 对于线性 SVM 和稀疏数据集最快。在现实世界的稀疏数据集上,SMO 的速度可以比分块算法快 1000 倍以上。
研究背景
在过去的几年中,学界对支持向量机(SVM)的研究兴趣激增,因其在诸如手写字符识别、面部检测、行人检测和文本分类等许多问题上均具有良好的泛化性能。然而,现有的 SVM 训练算法速度慢、内存开销大,且实现过于复杂和困难,这使得 SVM 的使用仍然仅限于一小部分研究人员。因此,为了提高 SVM 的实用性,亟需一种更好的训练算法。
问题描述
SVM 的训练本质上是求解一个二次规划(QP)问题,其拉格朗日对偶表示如下:
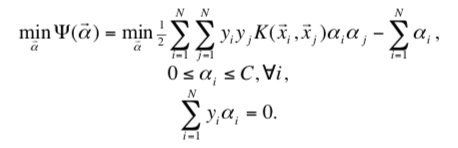
当满足如下 KKT 条件时,该 QP 问题得以解决:
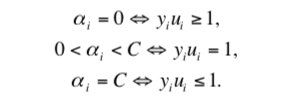
其中, x ⃗ i \vec x_i xi 是第 i 个训练样本, y i y_i yi 是第 i 个训练样本的真实标签, u i u_i ui 是第 i 个训练样本的输出, α i α_i αi 第 i 个训练样本对应的拉格朗日乘数, C C C 是惩罚参数。
上式中的二次形式涉及一个矩阵,该矩阵的元素数量等于训练样本数量的平方。一旦样本数量稍大,该矩阵将难以存入内存,因而通过标准的 QP 技术无法轻松解决由 SVM 引出的 QP 问题。
本文所讨论的内容即,作者所提出的训练算法是如何解决上述问题的。
研究现状
Vapnik[2] 描述了一种“分块”解决 SVM QP 的方法,将整个 QP 问题分解为多个 QP 子问题,其最终目标是识别所有非零拉格朗日乘数并丢弃所有零拉格朗日乘数。每个 QP 子问题都使用先前子问题的结果初始化。在最后一步,已经确定了整个非零拉格朗日乘数集,从而解决了整个 QP 问题。
分块处理将矩阵的大小从训练样本数的平方,减少到大约为非零拉格朗日乘数的数目的平方。然而,分块算法仍然不能解决大规模的训练问题,因为即使这个缩小的矩阵也无法放入内存中。
1997年,Osuna 等人[3] 从理论上证明,大的 QP 问题可以分解为一系列较小的 QP 子问题。基于此,论文建议在每一步中添加一个样本,然后去除一个样本,这样每个 QP 子问题将保持一个恒定大小的矩阵,从而允许对任意大小的数据集进行训练。但显然这是低效的,因为它使用整个数值 QP 优化步骤来仅仅使一个训练样本服从 KKT 条件。
更重要的是,所有这些方法都需要数值 QP 解算器,而众所周知,数值 QP 存在精度问题。
解决方法
作者在论文中提出的序列最小优化算法(SMO)是一种简单快速求解 SVM 引出的 QP 问题的方法,它将整个 QP 问题分解为多个 QP 子问题,通过 Osuna[3] 的定理保证收敛。
创新点与优势
不像以往的算法,SMO 在每一步仅选择两个拉格朗日乘数进行联合优化。其优势在于,两个拉格朗日乘数的优化可以通过解析方法完成,避免了数值 QP 优化,计算更快、更精确。此外,由于 SMO 完全不需要额外的矩阵存储,即使大规模的训练问题也可以在个人电脑的内存中运行。下图直观地说明了 SMO 与以往算法的区别。
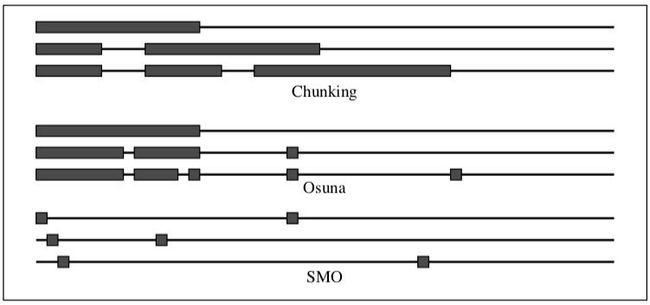
图中,每种算法均展示了三个训练轮次。水平细线代表训练集,粗块代表本轮中被优化的拉格朗日乘数。对于分块算法,每轮添加固定数量的样本,而为零的拉格朗日乘数被丢弃。因此,每轮的训练样本数量趋于增加。对于Osuna的算法,每轮都会优化固定数量的样本,因为添加和删除的样本数量相同。对于SMO,每轮都仅对两个样本进行解析优化,因此每轮都非常快。
实现过程
SMO 由两个部分组成:一种求解两个拉格朗日乘数的解析方法,以及一种选择要优化的乘数的启发式方法。
求解两个拉格朗日乘数的解析方法
为了求解两个拉格朗日乘数,SMO 首先计算这些乘数的约束,然后求解约束最小值。如下图所示,有界约束使拉格朗日乘数位于一个框内,而线性相等约束使拉格朗日乘数位于对角线上。 因此,目标函数的约束最小值必须位于对角线段上。
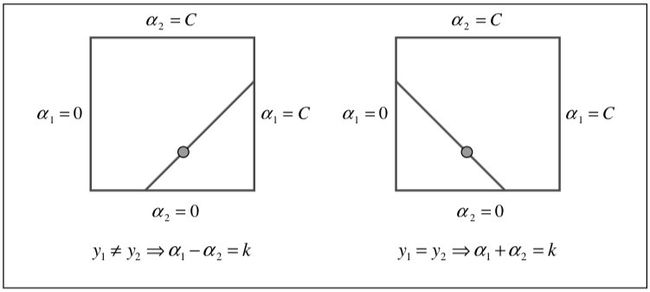
在实现上,假设当前为第 k k k 轮,使用解析法计算乘数 α 1 ( k ) α_1^{(k)} α1(k) 和 α 2 ( k ) α_2^{(k)} α2(k) 的最优解并更新至 α 1 ( k + 1 ) α_1^{(k+1)} α1(k+1) 和 α 2 ( k + 1 ) α_2^{(k+1)} α2(k+1), α ⃗ \vec α α 中的其他乘数不变,得到 α ⃗ ( k + 1 ) \vec α^{(k+1)} α(k+1),然后更新阈值 b ( k + 1 ) b^{(k+1)} b(k+1) 以及误差 $E_i^{(k+1)} $。具体计算过程如下:
-
计算 α 2 ( k + 1 ) α_2^{(k+1)} α2(k+1) 的取值范围 [ L , H ] [L, H] [L,H],其中

-
求得最优解 α 1 ( k + 1 ) α_1^{(k+1)} α1(k+1), α 2 ( k + 1 ) α_2^{(k+1)} α2(k+1), b ( k + 1 ) b^{(k+1)} b(k+1)

结合 α 2 ( k + 1 ) α_2^{(k+1)} α2(k+1) 的取值范围,可得

由 α 2 ( k + 1 ) α_2^{(k+1)} α2(k+1) 可求得 α 1 ( k + 1 ) α_1^{(k+1)} α1(k+1)

之后更新阈值 b b b
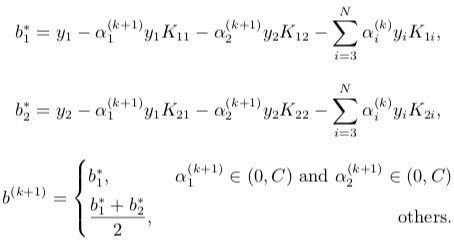
-
更新 E i E_i Ei 的值
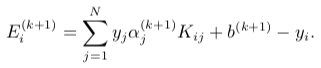
选择要优化的乘数的启发式方法
第一个乘数的选择称为外循环。首先遍历整个样本集,选择违反 KKT 条件的 α i α_i αi 作为第一个乘数,遍历完整个样本集后,遍历非边界样本集 0 < α i < C 0<α_i
第二个乘数的选择称为内循环。选择的依据是最大化联合优化过程中采取的步长,而 SMO 通过 ∣ E 1 − E 2 ∣ |E_1−E_2| ∣E1−E2∣ 来近似步长,为此需要为训练集中的每个非边界样本保留一个缓存的误差值 E i E_i Ei。
实验评估
作者对比标准分块 SVM 学习算法,对 SMO 算法进行了一系列基准测试。
实验平台
两种算法都以 C++ 编写,使用 Microsoft 的 Visual C++ 5.0 编译器,且都在运行 Windows NT 4 的 266 MHz Pentium II 处理器上运行。
实验配置
如 Burges[4] 的建议,分块算法使用投影共轭梯度算法[5]作为 QP 解算器,并使用启发式方法来设置停止阈值[1]。为了确保分块算法和 SMO 算法达到相同的精度,如果输出与其正确值相差 1 0 − 3 10^{-3} 10−3 以上,则两种算法都会将该样本标识为违反 KKT 条件。
实验方法
作者在收入预测任务、网页分类任务和两个不同的人工数据集上对 SMO 算法进行了测试,研究算法的时间性能以及数据稀疏性对运算速度的影响。以下表中列出的所有时间均以 CPU 秒为单位。
收入预测
用于测试 SMO 速度的第一个数据集是 UCI 的 adult 家庭普查数据集,共有 32562 个样本,包括 14 个属性。SVM 的任务是预测该家庭的收入是否超过 50,000 美元。针对该问题训练了两种不同的 SVM:线性 SVM 和方差为 10 的高斯SVM。
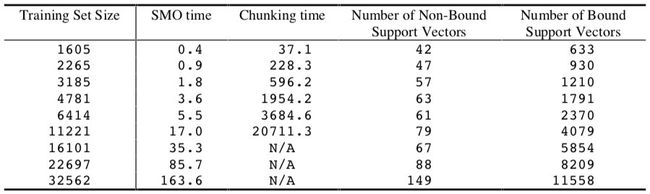
下表显示了在 adult 数据集上,使用 SMO 算法和分块算法训练线性 SVM 的时间。
通过拟合训练时间与训练集大小的对数-对数图,得出 SMO 的训练时间规模为 ~ N 1.9 N^{1.9} N1.9,而分块算法为 ~ N 3.1 N^{3.1} N3.1。因此,SMO将对于该问题的经验缩放比例优化了至少一个数量级。
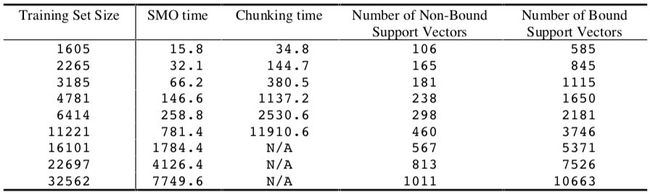
使用 SMO 算法和分块算法训练高斯 SVM 的时间如下表所示:
SMO 算法对于非线性 SVM 比线性 SVM 慢,这是因为时间开销主要由 SVM 的评估决定。这里,SMO 的训练时间规模为 ~ N 2.1 N^{2.1} N2.1,而分块算法为 ~ N 2.9 N^{2.9} N2.9。同样,SMO 比分块算法大约快一个数量级。
网页分类
SMO 的第二项测试是对网页进行分类。训练集包括 49749 个网页,从每个网页中提取了 300 个稀疏的二进制关键字属性。在此问题上尝试了两种不同的 SVM:线性 SVM 和方差为 10 的高斯 SVM。
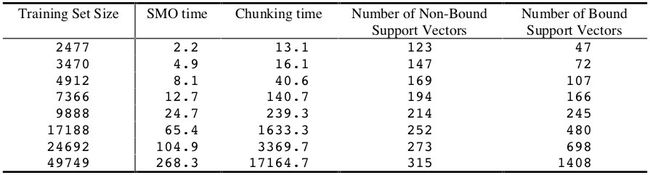
使用 SMO 算法和分块算法训练线性 SVM 的时间如下表所示:
对于该数据集上的线性 SVM,SMO 的训练时间规模为 ~ N 1.6 N^{1.6} N1.6,而分块算法为 ~ N 2.5 N^{2.5} N2.5。该实验是 SMO 在计算时间上优于分块算法的另一个例子。
使用 SMO 算法和分块算法训练高斯 SVM 的时间如下表所示:
对于该数据集上的非线性 SVM,SMO 的训练时间规模为 ~ N 1.7 N^{1.7} N1.7,而分块算法为 ~ N 2.0 N^{2.0} N2.0。在这种情况下,SMO 比分块算法快 2~6 倍。
线性可分数据集
作者还在人工生成的数据集上对 SMO 进行了测试,以探索 SMO 在极端情况下的性能。
第一个人工数据集是完全线性可分离的数据集,输入数据是随机二进制 300 维向量。这里用线性 SVM 拟合此数据集。
使用 SMO 算法和分块算法训练线性 SVM 的时间如下表所示:
SMO 的训练时间规模为 ~ N N N,较分块算法的 ~ N 1.2 N^{1.2} N1.2 稍好。
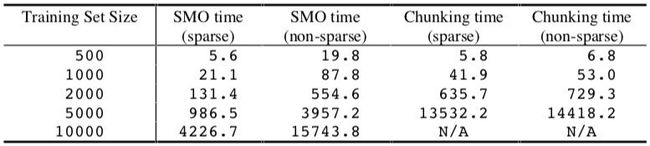
此外,还可以在此简单数据集上测量利用稀疏点积而获得的SMO算法和分块算法的加速。相同的数据集在使用和不使用稀疏点乘积代码的情况下都进行了测试。
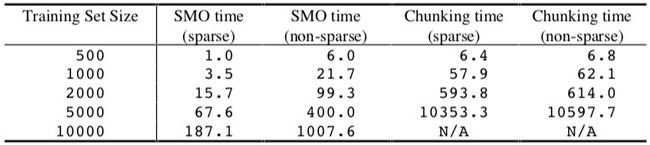
稀疏/非稀疏实验的结果如下表所示:
对于 SMO,使用稀疏数据结构将代码的速度提高了 10 倍以上,这表明 SVM 的评估时间完全决定了 SMO 的计算时间。稀疏点积代码仅将分块算法的速度提高了大约 1.1 倍,这表明数值 QP 步骤的评估在分块计算中占主导地位。
噪声数据集
第二个人工数据集由随机的 300 维二进制输入点和随机输出标签生成。SVM 拟合的是纯噪声。
将 SMO 和分块算法应用于线性 SVM 的结果如下所示:
SMO 的计算时间规模为 ~ N 1.8 N^{1.8} N1.8,而分块算法为 ~ N 3.2 N^{3.2} N3.2。该结果显示,当大多数支持向量都处于边界时,SMO 表现出色。因此,为了确定由稀疏点积代码引起的速度增加,在没有使用稀疏点乘积代码的情况下测试了 SMO 和分块算法:
在线性 SVM 情况下,稀疏点积代码将 SMO 的速度提高了大约 6 倍,而分块算法的速度提升很小。在该实验中,即使对于非稀疏数据,SMO 也比分块更快。
同样地,作者也使用了方差为 10 的高斯 SVM 对第二个人工数据集进行了测试,实验结果显示在以下两个表格中:
对于拟合纯噪声的高斯 SVM,SMO 的计算时间规模为 ~ N 2.2 N^{2.2} N2.2,而分块算法为 ~ N 3.4 N^{3.4} N3.4。即使应用于非稀疏数据,SMO 的总运行时间仍然优于分块算法。对于非线性情况,输入数据的稀疏性使 SMO 的速度提高了大约 4 倍,这表明对于非线性 SVM,点积速度仍占 SMO 计算时间的主导地位。
实验结论
- SMO 在多种不同的数据集上都比分块算法更快。
- SMO 在有许多拉格朗日乘数处于边界上的 SVM 上表现出色。
- SMO 对于线性 SVM 表现良好,因为 SMO 的计算时间主要由 SVM 评估决定。
- SMO 对于具有稀疏输入的 SVM 表现出色(即使是非线性 SVM),因为其可以减少核函数的计算时间,从而直接加速了 SMO。
- SMO 在大规模问题上表现良好,因为对于文中所有的测试问题,其计算时间随训练集大小的缩放规模都优于分块算法。
不足之处
S.S. Keerthi 等人[6]指出,由于 SMO 的计算方式以及仅维护和更新一个阈值 β β β 的特点,在某些情况下可能会进行不必要的第二个拉格朗日乘数的搜索,从而导致 SMO 的效率低下。
左琳[7]也指出,SMO 实际上是在循环迭代上寻求快速算法。因此如果没有一个好的选择迭代策略,SMO 算法就存在盲目性,可能出现某些达到最优值的样本却不满足 KKT 条件的情况,比如过度选择的消耗,影响了算法的执行效率。
参考文献
- J. Platt, “Sequential minimal optimization: A fast algorithm for training support vector machines,” Microsoft, Res. Tech. Rep. MSR-TR-98-14, 1998.
- Vapnik, V., Estimation of Dependences Based on Empirical Data, Springer-Verlag, (1982).
- Osuna, E., Freund, R., Girosi, F., “Improved Training Algorithm for Support Vector Machines,” Proc. IEEE NNSP ’97, (1997).
- Burges, Christopher JC. “A tutorial on support vector machines for pattern recognition.” Data mining and knowledge discovery 2.2 (1998): 121-167.
- Gill, P. E., Murray, W., Wright, M. H., Practical Optimization, Academic Press, (1981).
- Keerthi, S. Sathiya, et al. “Improvements to Platt’s SMO algorithm for SVM classifier design.” Neural computation 13.3 (2001): 637-649.
- 左琳. “序列最小优化工作集选择算法的改进.” 电子科技大学学报 42.3 (2013): 448-451.