默克尔树(Merkle Tree)总结
目录
为什么要有默克尔树
简介
Merkle Tree的特点
图解
创建树
检索-文件夹比较
检索-防伪
更新
插入删除
应用
数字签名
P2P网络
可信计算
区块链-简单验证支付
为什么要有默克尔树
Hash是一个把任意长度的数据映射成固定长度数据的函数[2]。例如,对于数据完整性校验,最简单的方法是对整个数据做Hash运算得到固定长度的Hash值,然后把得到的Hash值公布在网上,这样用户下载到数据之后,对数据再次进行Hash运算,比较运算结果和网上公布的Hash值进行比较,如果两个Hash值相等,说明下载的数据没有损坏。可以这样做是因为输入数据的稍微改变就会引起Hash运算结果的面目全非,而且根据Hash值反推原始输入数据的特征是困难的。
如果从一个稳定的服务器进行下载,采用单一Hash是可取的。但如果数据源不稳定,一旦数据损坏,就需要重新下载,这种下载的效率是很低的。
在点对点网络中作数据传输的时候,会同时从多个机器上下载数据,而且很多机器可以认为是不稳定或者不可信的。为了校验数据的完整性,更好的办法是把大的文件分割成小的数据块(例如,把分割成2K为单位的数据块)。这样的好处是,如果小块数据在传输过程中损坏了,那么只要重新下载这一快数据就行了,不用重新下载整个文件。
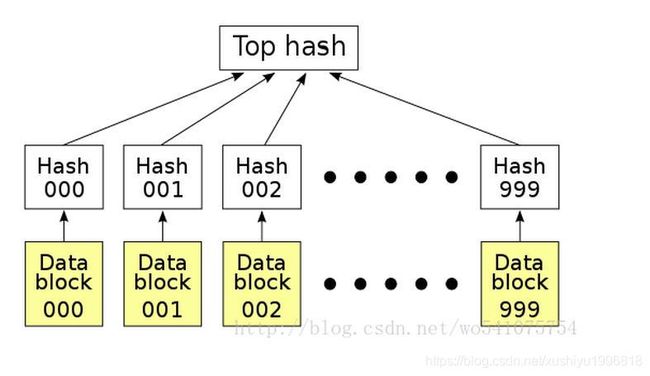
怎么确定小的数据块没有损坏哪?只需要为每个数据块做Hash。BT下载的时候,在下载到真正数据之前,我们会先下载一个Hash列表。那么问题又来了,怎么确定这个Hash列表本事是正确的哪?答案是把每个小块数据的Hash值拼到一起,然后对这个长字符串在作一次Hash运算,这样就得到Hash列表的根Hash(Top Hash or Root Hash)。下载数据的时候,首先从可信的数据源得到正确的根Hash,就可以用它来校验Hash列表了,然后通过校验后的Hash列表校验数据块。
简介
默克尔树,Merkle Tree可以看做Hash List的泛化(Hash List可以看作一种特殊的Merkle Tree,即树高为2的多叉Merkle Tree)。
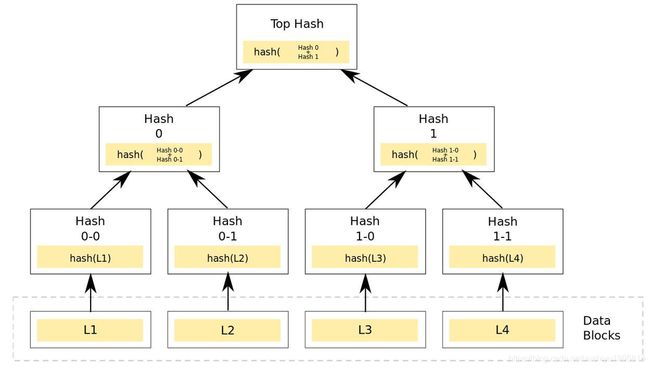
在最底层,和哈希列表一样,我们把数据分成小的数据块,有相应地哈希和它对应。但是往上走,并不是直接去运算根哈希,而是把相邻的两个哈希合并成一个字符串,然后运算这个字符串的哈希,这样每两个哈希就结婚生子,得到了一个”子哈希“。如果最底层的哈希总数是单数,那到最后必然出现一个单身哈希,这种情况就直接对它进行哈希运算,所以也能得到它的子哈希。于是往上推,依然是一样的方式,可以得到数目更少的新一级哈希,最终必然形成一棵倒挂的树,到了树根的这个位置,这一代就剩下一个根哈希了,我们把它叫做 Merkle Root[3]。
在p2p网络下载网络之前,先从可信的源获得文件的Merkle Tree树根。一旦获得了树根,就可以从其他从不可信的源获取Merkle tree。通过可信的树根来检查接受到的Merkle Tree。如果Merkle Tree是损坏的或者虚假的,就从其他源获得另一个Merkle Tree,直到获得一个与可信树根匹配的Merkle Tree。
Merkle Tree和Hash List的主要区别是,可以直接下载并立即验证Merkle Tree的一个分支。因为可以将文件切分成小的数据块,这样如果有一块数据损坏,仅仅重新下载这个数据块就行了。如果文件非常大,那么Merkle tree和Hash list都很到,但是Merkle tree可以一次下载一个分支,然后立即验证这个分支,如果分支验证通过,就可以下载数据了。而Hash list只有下载整个hash list才能验证。
Merkle Tree的特点
MT是一种树,大多数是二叉树,也可以多叉树,无论是几叉树,它都具有树结构的所有特点;
Merkle Tree的叶子节点的value是数据集合的单元数据或者单元数据HASH。默克尔树的基础数据不是固定的,想存什么数据由你说了算,因为它只要数据经过哈希运算得到的hash值。
非叶子节点的value是根据它下面所有的叶子节点值,然后按照Hash算法计算而得出的。默克尔树是从下往上逐层计算的,就是说每个中间节点是根据相邻的两个叶子节点组合计算得出的,而根节点是根据两个中间节点组合计算得出的,所以叶子节点是基础。
图解
创建树
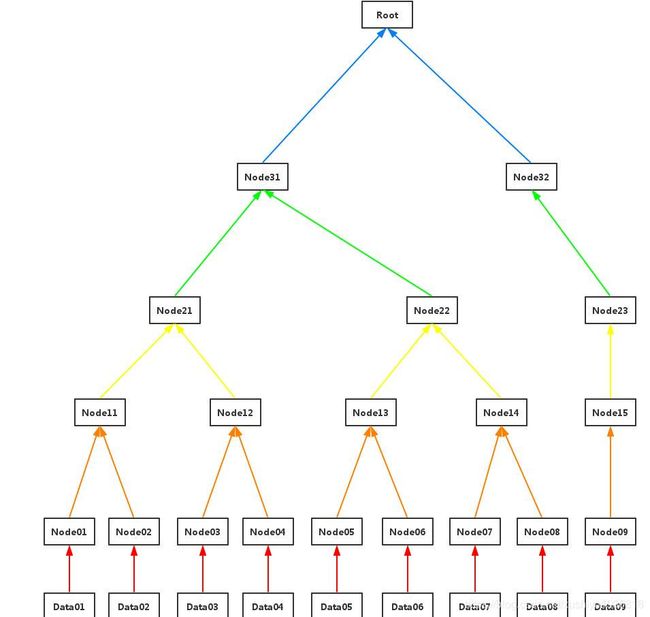
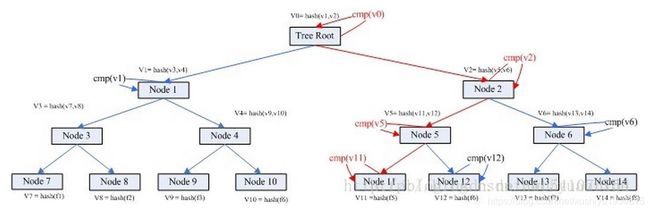
加入最底层有9个数据块。
step1:(红色线)对数据块做hash运算,Node0i = hash(Data0i), i=1,2,…,9
step2: (橙色线)相邻两个hash块串联,然后做hash运算,Node1((i+1)/2) = hash(Node0i+Node0(i+1)), i=1,3,5,7;对于i=9, Node1((i+1)/2) = hash(Node0i)
step3: (黄色线)重复step2
step4:(绿色线)重复step2
step5:(蓝色线)重复step2,生成Merkle Tree Root
检索-文件夹比较
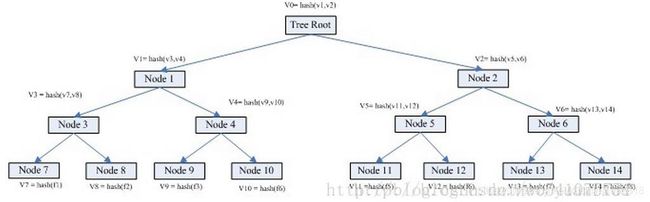
为了更好理解,我们假设有A和B两台机器,A需要与B相同目录下有8个文件,文件分别是f1 f2 f3 ….f8。这个时候我们就可以通过Merkle Tree来进行快速比较。假设我们在文件创建的时候每个机器都构建了一个Merkle Tree。具体如下图:
从上图可得知,叶子节点node7的value = hash(f1),是f1文件的HASH;而其父亲节点node3的value = hash(v7, v8),也就是其子节点node7 node8的值得HASH。就是这样表示一个层级运算关系。root节点的value其实是所有叶子节点的value的唯一特征。
假如A上的文件5与B上的不一样。我们怎么通过两个机器的merkle treee信息找到不相同的文件? 这个比较检索过程如下:
Step1. 首先比较v0是否相同,如果不同,检索其孩子node1和node2.
Step2. v1 相同,v2不同。检索node2的孩子node5 node6;
Step3. v5不同,v6相同,检索比较node5的孩子node 11 和node 12
Step4. v11不同,v12相同。node 11为叶子节点,获取其目录信息。
Step5. 检索比较完毕。
以上过程的理论复杂度是Log(N)。过程描述图如下:
检索-防伪
如果一个恶意的 用户试图在默克尔树的底部替换一个假的交易, 这个更改将导致上面的节点发生变化,然后上面的节点的变化又会导致上上面的节点发生变化,最终改变这个数根节点,因此也改变了这区块的哈 希,导致这个协议把它注册成一个完全不同的区块 (几乎可以肯定是一个无效的工作证明).
更新
对于Merkle Tree数据块的更新操作其实是很简单的,更新完数据块,然后接着更新其到树根路径上的Hash值就可以了,这样不会改变Merkle Tree的结构。
插入删除
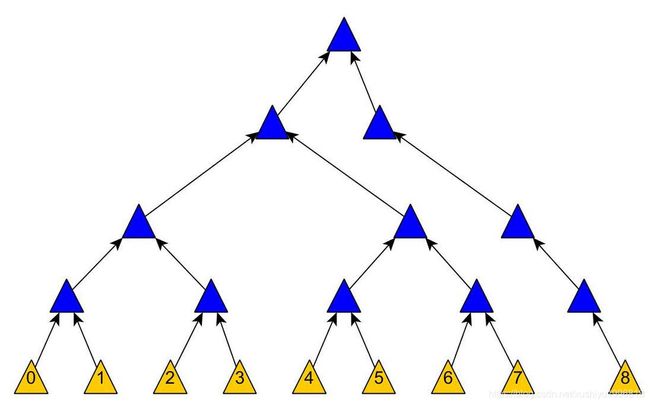
这是原来的默克尔树,总共8个叶子节点,现在插入节点0
有两种办法
死办法
生成平衡树的方法
Merkle Tree的插入和删除操作其实是一个工程上的问题,不同问题会有不同的插入方法。如果要确保树是平衡的或者是树高是log(n)的,可以用任何的标准的平衡二叉树的模式,如AVL树,红黑树,伸展树,2-3树等。这些平衡二叉树的更新模式可以在O(lgn)时间内完成插入操作,并且能保证树高是O(lgn)的。那么很容易可以看出更新所有的Merkle Hash可以在O((lgn)2)时间内完成(对于每个节点如要更新从它到树根O(lgn)个节点,而为了满足树高的要求需要更新O(lgn)个节点)。如果仔细分析的话,更新所有的hash实际上可以在O(lgn)时间内完成,因为要改变的所有节点都是相关联的,即他们要不是都在从某个叶节点到树根的一条路径上,或者这种情况相近。
实际上Merkle Tree的结构(是否平衡,树高限制多少)在大多数应用中并不重要,而且保持数据块的顺序也在大多数应用中也不需要。因此,可以根据具体应用的情况,设计自己的插入和删除操作。一个通用的Merkle Tree插入删除操作是没有意义的。(因为一般默克尔树根据它的应用和特性,只有创建和检索操作)
应用
数字签名
最初Merkle Tree目的是高效的处理Lamport one-time signatures。 每一个Lamport key只能被用来签名一个消息,但是与Merkle tree结合可以来签名多条Merkle。这种方法成为了一种高效的数字签名框架,即Merkle Signature Scheme。
P2P网络
在P2P网络中,Merkle Tree用来确保从其他节点接受的数据块没有损坏且没有被替换,甚至检查其他节点不会欺骗或者发布虚假的块。大家所熟悉的BT下载就是采用了P2P技术来让客户端之间进行数据传输,一来可以加快数据下载速度,二来减轻下载服务器的负担。BT即BitTorrent,是一种中心索引式的P2P文件分分析通信协议。
要进下载必须从中心索引服务器获取一个扩展名为torrent的索引文件(即大家所说的种子),torrent文件包含了要共享文件的信息,包括文件名,大小,文件的Hash信息和一个指向Tracker的URL。Torrent文件中的Hash信息是每一块要下载的文件内容的加密摘要,这些摘要也可运行在下载的时候进行验证。大的torrent文件是Web服务器的瓶颈,而且也不能直接被包含在RSS或gossiped around(用流言传播协议进行传播)。一个相关的问题是大数据块的使用,因为为了保持torrent文件的非常小,那么数据块Hash的数量也得很小,这就意味着每个数据块相对较大。大数据块影响节点之间进行交易的效率,因为只有当大数据块全部下载下来并校验通过后,才能与其他节点进行交易。
就解决上面两个问题是用一个简单的Merkle Tree代替Hash List。设计一个层数足够多的满二叉树,叶节点是数据块的Hash,不足的叶节点用0来代替。上层的节点是其对应孩子节点串联的hash。Hash算法和普通torrent一样采用SHA1。其数据传输过程和第一节中描述的类似。 ![]()
可信计算
可信计算是可信计算组为分布式计算环境中参与节点的计算平台提供端点可信性而提出的。可信计算技术在计算平台的硬件层引入可信平台模块(Trusted Platform,TPM),实际上为计算平台提供了基于硬件的可信根(Root of trust,RoT)。从可信根出发,使用信任链传递机制,可信计算技术可对本地平台的硬件及软件实施逐层的完整性度量,并将度量结果可靠地保存再TPM的平台配置寄存器(Platform configuration register,PCR)中,此后远程计算平台可通过远程验证机制(Remote Attestation)比对本地PCR中度量结果,从而验证本地计算平台的可信性。可信计算技术让分布式应用的参与节点摆脱了对中心服务器的依赖,而直接通过用户机器上的TPM芯片来建立信任,使得创建扩展性更好、可靠性更高、可用性更强的安全分布式应用成为可能[10]。可信计算技术的核心机制是远程验证(remote attestation),分布式应用的参与结点正是通过远程验证机制来建立互信,从而保障应用的安全。 ![]()
文献提出了一种基于Merkle Tree的远程验证机制,其核心是完整性度量值哈希树。
首先,RAMT 在内核中维护的不再是一张完整性度量值列表(ML),而是一棵完整性度量值哈希树(integrity measurement hash tree,简称IMHT).其中,IMHT的叶子结点存储的数据对象是待验证计算平台上被度量的各种程序的完整性哈希值,而其内部结点则依据Merkle 哈希树的构建规则由子结点的连接的哈希值动态生成。
其次,为了维护IMHT 叶子结点的完整性,RAMT 需要使用TPM 中的一段存储器来保存IMHT 可信根哈希的值。
再次,RAMT 的完整性验证过程基于认证路径(authentication path)实施.认证路径是指IMHT 上从待验证叶子结点到根哈希的路径。
区块链-简单验证支付
中本聪在他的创世论文中一个概念,就是SPV,中文意思是简单支付验证,从这里我们可以看出SPV指的是“支付验证”而不是“交易验证”,那这两者有什么区别吗?简单的说就是支付验证只需验证该笔交易是否被确认过了,而交易验证是需要验证该笔交易是否满足一些条件如“余额”是否足够,还有该笔交易有没有存在双花等等一些问题,只有一切都没什么问题后该笔交易才算验证通过,可以看出交易验证要比支付验证更加复杂,所以它一般是由挖矿节点来完成的,而支付验证只要普通的轻钱包就可以完成。那现在有一个问题了,SPV是如何实现的?答案就是默克尔树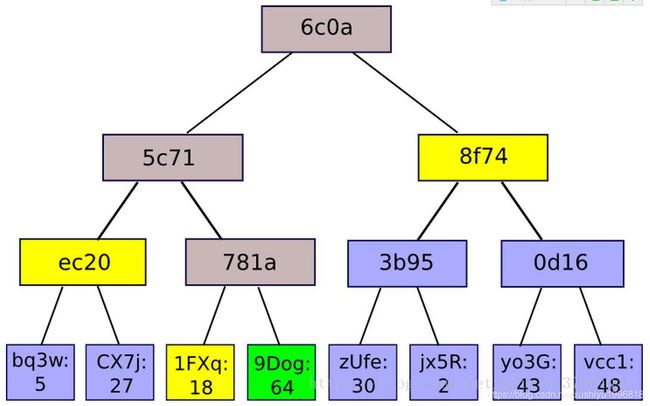
假设我们要验证区块中存在Hash值为9Dog:64(绿色框)的交易,我们仅需要知道1FXq:18、ec20、8f74(黄色框)即可计算出781a、5c71与Root节点(藕粉色框)的哈希,如果最终计算得到的Root节点哈希与区块头中记录的哈希(6c0a)一致,即代表该交易在区块中存在。这是因为我上文提到的两个点,一个是默克尔树是从下往上逐层计算的,所以只要知道相邻的另一个节点的hash值就可以一直往上计算直到根节点,另一个是根节点的hash值可以准确的作为一组交易的唯一摘要,依据这两点就可以来验证一笔交易是否存在。