神经网络学习（四）反向（BP）传播算法（2）-Matlab实现
系列博客是博主学习神经网络中相关的笔记和一些个人理解，仅为作者记录笔记之用，不免有很多细节不对之处。
回顾
上一小节我们讨论了BP算法的推导，如果我们采用均方误差作为代价函数，那么4个基础方程如下：
这一小节，我们来看看BP神经网络的一个Matlab简单实现（博主是Matlab重度依赖患者）。
数据准备
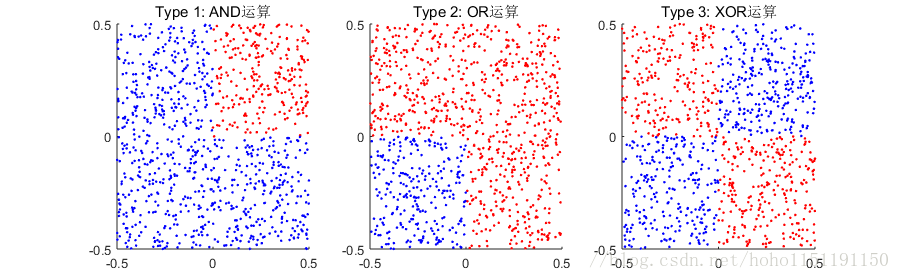
在正式开始前，我们先准备用来测试咱们的神经网络是否正确的数据。为了方便可视化，数据限定为二维，数值大小在[-1,1]之间。按照这个限制设计了以下几个数据模式（生成函数为 generateData）:
上面这三种模式，分别对应着逻辑AND运算，逻辑OR操作和逻辑XOR操作。红色代表1，蓝色代表0。
这四种模式就是简单的分段函数。
上面这三种是极坐标中的分段函数，然后转换到直角坐标系的。
BP算法
本节所有程序代码可在这里下载
BP算法是针对一个样本进行的，在模型参数更新时，我们对mini_batch的偏导数进行平均。激活函数我们选用Sigmoid函数(函数名sigmoid)，它的导数为 f(x)(1−f(x)) f ( x ) ( 1 − f ( x ) ) (函数名sigmoid_prime)。
%神经网络的层次
arch = [2,30,1];
nlayer = length(arch);
%随机梯度下降法，小批量数据大小
mini_batch_size = 200;% 最大迭代次数
max_epochs = 2000;% 学习速率
zeta = 20;
%神经网络参数以及初始化
weight = cell(1,nlayer);
bias = cell(1,nlayer);
nabla_weight = cell(1,nlayer); %存放权重的偏导数
nabla_bias = cell(1,nlayer); %存放偏置的偏导数
a = cell(1,nlayer); %存放每个神经元的输出
z = cell(1,nlayer); %存放带权输入
%参数初始化，第一层为输入层，没有权重，为了方便下标从第2层开始
for in = 2:nlayer
weight{in} = rand(arch(in),arch(in-1))-0.5;
bias{in} = rand(arch(in),1);
nabla_weight{in} = rand(arch(in),arch(in-1));
nabla_bias{in} = rand(arch(in),1);
end
for in = 1:nlayer
a{in} = zeros(arch(in),mini_batch_size);
z{in} = zeros(arch(in),mini_batch_size);
end
accuracy = zeros(1,max_epochs);
%主循环
for ip = 1:max_epochs
%随机选取数据
pos = randi(ntrain-mini_batch_size);
x = x_train(:,pos+1:pos+mini_batch_size);
y = y_train(pos+1:pos+mini_batch_size);
%正向计算
a{1} = x;
[a,z]=feedforward(weight,bias,nlayer,mini_batch_size,a,z);
%随机梯度
[weight,bias] = SGD(weight,bias,nabla_weight,nabla_bias,nlayer,mini_batch_size,zeta,a,z,y);
%实时显示精度，利用test数据进行测试
%accuracy(ip) = evaluate(x_test,y_test,weight,bias,nlayer);
%plot(accuracy);
%title(['Accuracy: ',num2str(accuracy(ip))]);
%getframe;
end
[ac,yp]=evaluate(x_test,y_test,weight,bias,nlayer);
figure
subplot(1,2,1)
plotData(x_test,y_test,'测试数据')
subplot(1,2,2)
plotData(x_test,yp,'预测结果');
主程序没有什么复杂的地方。关键在于要充分利用Matlab矩阵乘法的高效性。在每一次迭代过程中要一次性计算整个mini_batch的偏导数。下面是关键函数feedforward的代码。正演过程是逐层进行的，w*x能够一次性计算完整个mini_batch，可以大幅度提高计算效率。在计算过程中还要保存激活值 a a 和带权输入 z z ，这两个量要在反向计算中使用。
function [a,z] = feedforward(weight,bias,nlayer,mini_batch_size,a,z)
%FEEDFORWARD Return the output of the network
%
%一层一层计算。
for in = 2:nlayer
w = weight{in};
b = bias{in};
ix = a{in-1};
%w*ix可以一次性全部计算完整个mini_batch
iz = w*ix;
%无法直接利用w*ix+b的运算，b并没有定义和二维数据的形式
%想利用这个算式，可以用repmat函数
for im = 1:mini_batch_size
iz(:,im) = iz(:,im)+b;
end
a{in} = sigmoid(iz);
z{in} = iz;
end
end下面是关键函数SGD的代码。反演过程是从最后一层逐层递减进行的，基本上是直白的翻译公式BP1-4。一个小技巧是计算权值的偏导数时利用了矩阵的乘法实现mini_batch的求和平均的。
function [weight,bias] = SGD(weight,bias,nabla_weight,nabla_bias,nlayer,mini_batch_size,zeta,a,z,y)
%SGD stochastic gradient descent
%
%计算输出层的误差delta，即公式BP1
delta = (a{nlayer}-y).*sigmoid_prime(z{nlayer});
nabla_bias{end} = mean(delta,2);
nabla_weight{end} = (delta*a{end-1}')/mini_batch_size;
%逐层递减进行
for in = nlayer-1:-1:2
%公式BP2
delta = weight{in+1}'*delta.*sigmoid_prime(z{in});
%公式BP3
nabla_bias{in} = mean(delta,2);
%公式BP4,注意a和delta的位置，利用矩阵乘法
nabla_weight{in} = (delta*a{in-1}')/mini_batch_size;
end
%网络参数更新
for in = 2:nlayer
weight{in} = weight{in} - zeta*nabla_weight{in};
bias{in} = bias{in} - zeta*nabla_bias{in};
end
end三个例子：
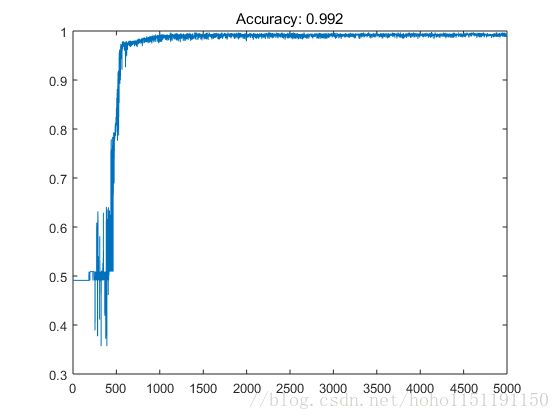
模式8数据，学习速率20，子数据集大小为200，迭代次数为5000次，精度大约99%，精度曲线和测试结果如下:
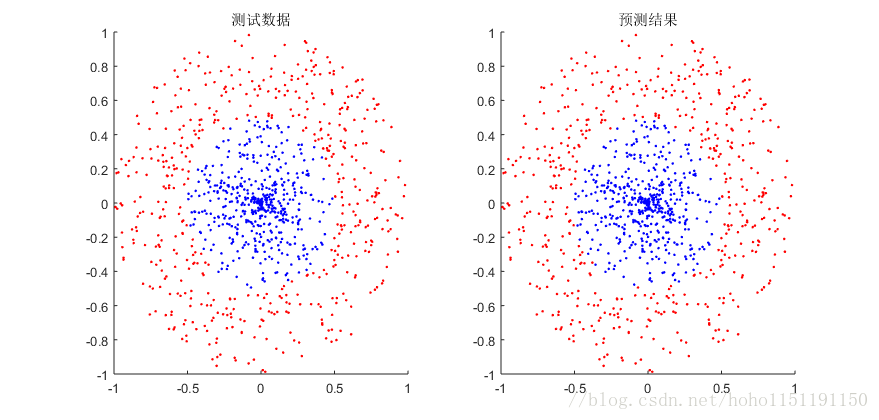
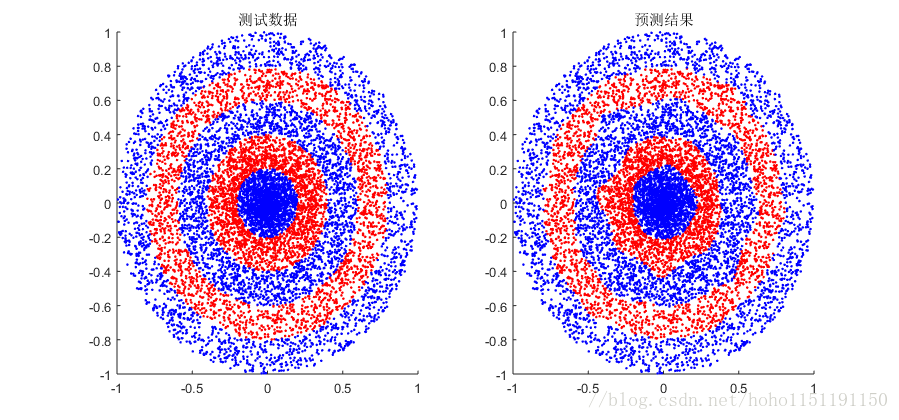
模式10数据，学习速率20，训练数据6000，测试数据1000，子数据集大小为200，迭代次数为100000次。对于这个模式数据，迭代次数少了基本无法预测，测试结果如下：:
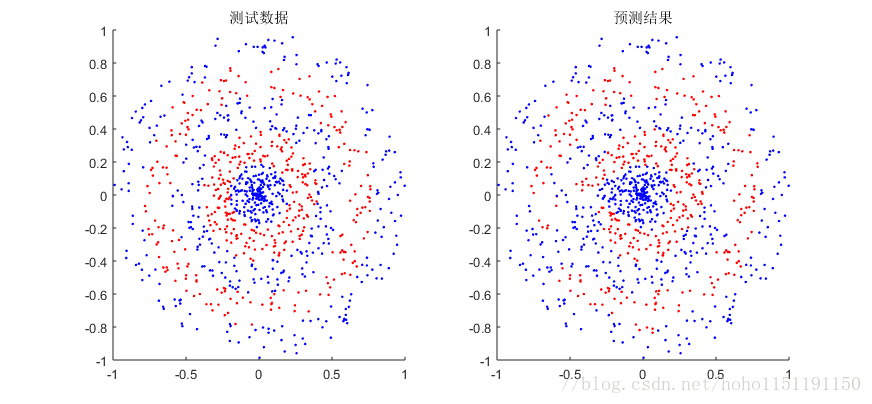
模式10数据，学习速率20，训练数据10000，测试数据10000，子数据集大小为2000，迭代次数为100000次。相比上一个测试，数据量增大了，预测效果变好，测试结果如下：:
