浅谈Dijkstra与堆优化

首先感谢学长们的算法课！在七次课程中我总算是迈开了算法学习的第一步。然而因个人能力实在有限，有些知识没能很好地掌握。这次我将选取自己比较熟悉的Dijkstra算法进行整理。（因个人原因我对c++以及数据结构的大部分内容都比较陌生，所以博客中的错误还请各位多指正）

浅谈Dijkstra

1.解决问题

Dijkstra算法解决的是有权图的最短路径问题（指定两点间的最短路径，或指定点到其他所有点的最短路径）。需要注意的是，Dijkstra算法不适用于图存在负边的情况。

2.基本思想

贪心+动态规划

dis[i]：初始点到图上点i的距离（初始值：与初始点相邻的点dis值为边的权值，若不相邻，则为∞）。
visit[i]：图上点i是否已被最短路径经过（个人的理解是，当该节点已作为一个中间节点，在初始点到其他节点的路径上被经过时，使该节点的visit布尔值为true。仅在visit值为false中的节点寻找最小的dis值，是因为经过的节点无需经过第二次。）

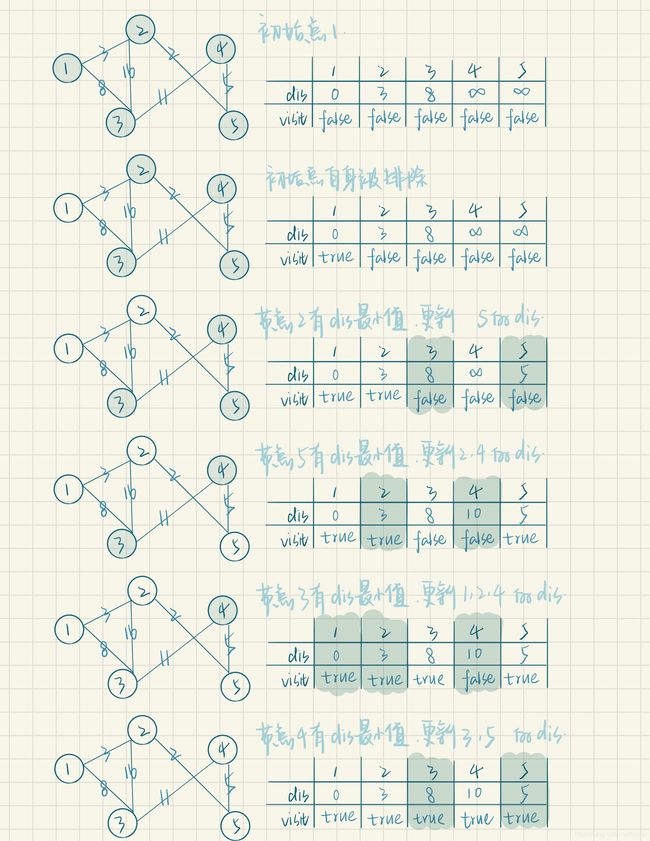
1） 初始化：初始点s有dis[s]=0, 与初始点相邻的点dis值为边的权值，若不相邻，则为∞。所有点visit值都为false。
2） 在所有visit值为false的节点中找到一个dis值最小的，节点记作x。若所有visit值都为true，则算法结束。
3） 标记visit[x]=true,用x到相邻点距离更新与x相邻点的dis值：
dis[y] = min {dis[y] , dis[y] + w(x ,y ) }
其中y为x的相邻点，w
( x , y ) 为x ->y这条有有向边的权值(如果x，y不直接相邻，则令w（x，y）=∞)。

图示：

3.代码

以上图为例

输入：
5 6
2 3
1 3 8
2 3 16
2 5 2
3 4 11
4 5 5

#include
#include
#include
#include
#include
using namespace std;
struct node 
{
 int to;
 int w;
};
int n, m;
int edgeNum[100];
int dis[100];
bool vis[100];
vector vec[100];
void addEdge(int a, int b, int w)//给节点a添加一条边
{
 edgeNum[a]++;
 node *p = new node();
 p->to = b;
 p->w = w;
 vec[a].push_back(*p);
}
void init()
{
 cin >> n >> m;
 for (int i = 1; i <= m; i++)
 {
  int a, b, w;
  cin >> a >> b >> w;
  addEdge(a, b, w);
  addEdge(b, a, w);//这里应该是针对无向边
 }
}
void dijkstra_1(int start)
{
 memset(dis, 0x3f, sizeof(dis));//各点到初始点距离初始化为极大
 dis[start] = 0;
 for(int i = 0; i < edgeNum[start]; i++)
 {
  int b = vec[start][i].to;
  int w = vec[start][i].w;
  dis[b] = w;//与初始点相邻的节点dis值初始化为边权值
 }
 vis[start] = true;
 for (int k = 1; k < n; k++)//外循环，确认所有节点都被经过
 {
  int minV = 0x7fffffff, min_i;
  for (int i = 1; i <= n; i++)//寻找未经过节点中dis值最小的点
   if (!vis[i] && dis[i] < minV)
   {
    minV = dis[i];
    min_i = i;
   }
  vis[min_i] = true;//将该节点标记为已经过
  for (int i = 0; i < edgeNum[min_i]; i++)//更新与该节点相邻节点的dis值
  {                                    
   int b = vec[min_i][i].to;
   int w = vec[min_i][i].w;
   if (dis[b] > (dis[min_i] + w))
    dis[b] = dis[min_i] + w;//确保最短路径的子路径也是最短路径
  }
 }
}
void print()
{
 for (int i = 1; i <= n; i++)
  cout << dis[i] << " ";
 cout << endl;
}
int main()
{
 init();
 dijkstra_1(1);
 print();
 system("pause");
 return 0;
}

（代码有参考）
输出结果：
0 3 8 10 5

例题

Hdu 2066 一个人的旅行

Problem Description

虽然草儿是个路痴（就是在杭电待了一年多，居然还会在校园里迷路的人，汗~),但是草儿仍然很喜欢旅行，因为在旅途中
会遇见很多人（白马王子），很多事，还能丰富自己的阅历，还可以看美丽的风景……草儿想去很多地方，她想要去东京铁塔看夜景，去威尼斯看电影，去阳明山上看海芋，去纽约纯粹看雪景，去巴黎喝咖啡写信，去北京探望孟姜女……眼看寒假就快到了，这么一大段时间，可不能浪费啊，一定要给自己好好的放个假，可是也不能荒废了训练啊，所以草儿决定在要在最短的时间去一个自己想去的地方！因为草儿的家在一个小镇上，没有火车经过，所以她只能去邻近的城市坐火车（好可怜啊~）。

Input
输入数据有多组，每组的第一行是三个整数T，S和D，表示有T条路，和草儿家相邻的城市的有S个，草儿想去的地方有D个；
接着有T行，每行有三个整数a，b，time,表示a,b城市之间的车程是time小时；(1=<(a,b)<=1000;a,b 之间可能有多条路)
接着的第T+1行有S个数，表示和草儿家相连的城市；
接着的第T+2行有D个数，表示草儿想去地方。
Output
输出草儿能去某个喜欢的城市的最短时间。

Sample Input
6 2 3
1 3 5
1 4 7
2 8 12
3 8 4
4 9 12
9 10 2
1 2
8 9 10
Sample Output
9

分析：
1.题目看似是求多源最短路，实际上只要将小草家看作源点，即可将问题转化为单源最短路问题。而去喜欢的城市最短时间时也可添加一个终点，使喜欢的城市连接到同一个终点上，然后使连接的路径耗时为零，最终输出终点的最短时间即可。
2.题目中也有说明城镇之间有不止一条路径，故要选择最短路径耗时作为最终耗时。

代码（这里选择用矩阵来存储图，该方法会有较多冗余，一般建议使用邻接表）

#include
#include
#include
#include
#pragma warning(disable:4996)
using namespace std;
const int inf = 1 << 20;
const int maxn = 1005;
int T, S, D, N;
int map[maxn][maxn], dis[maxn];
int vis[maxn];
int max(int a, int b)
{
 return a = (a > b ? a : b);
}
void init()
{
 for (int i = 0; i < maxn; i++)
  for (int j = 0; j < maxn; j++)
   map[i][j] = (i == j ? 0 : inf);
 int a, b, w;
 N = 0;
 for (int i = 0; i < T; i++)
 {
  cin >> a >> b >> w;
  if (map[a][b] > w)
   map[a][b] = map[b][a] = w;
  N = max(N, max(a, b));
 }
 N++;
 for (int i = 0; i < S; i++)
 {
  int a;
  cin >> a;
  map[0][a] = map[a][0] = 0;
 }
 for (int i = 0; i < D; i++)
 {
  int a;
  cin >> a;
  map[a][N] = map[N][a] = 0;
 }
}
void dijkstra(int start)
{
 for (int i = 0; i <= N; i++)
  dis[i] = map[0][i];
 memset(vis, 0, sizeof(vis));
 for (int i = 0; i <= N; i++)
 {
  int minV = inf;
  int min_j=-1;
  for(int j=0;j<=N;j++)
   if (!vis[j] && dis[j] < minV)
   {
    minV = dis[j];
    min_j = j;
   }
  if (min_j == -1)
   break;
  else vis[min_j] = 1;
     if (dis[j] > (dis[min_j] + map[min_j][j]))
    dis[j] = dis[min_j] + map[min_j][j];
 }
}
int main()
{
 while (scanf("%d %d %d",&T,&S,&D)!=EOF)
 {
  init();
  dijkstra(0);
  printf("%d\n", dis[N]);
 }
 system("pause");
 return 0;
}

（代码有参考）

堆优化

基本要点

1. 使用优先队列，可以直接弹出dis值最小的节点（用结构体重载括号运算符来实现），省略了查找最小dis值的过程。
2. 更新过的节点则重新压入队列尾部。

代码

优先队列及改造

struct qnode 
{
 int i_i;
 int dis_i;
 qnode(int i, int dis_i) 
 {
  this->i_i = i;
  this->dis_i = dis_i;
 }
};
struct cmp //重载运算符
{
 bool operator()(const qnode &x, const qnode &y)
 {
  return x.dis_i > y.dis_i;//将dis值作为比较的对象
 }
};
priority_queue, cmp> q;//队列顶端是dis值最小的节点

Dijkstra

void dijkstra_2(int start)
{
 memset(dis, 0x3f, sizeof(dis));
 dis[start] = 0;
 q.push(qnode(start, dis[start]));
 while (!q.empty())//！！重点
 {
  qnode p = q.top();
  q.pop();
  int min_i = p.i_i;
  int minV = p.dis_i;
        if (vis[min_i]) continue;
  vis[min_i] = true;
  for (int i=0; i < edgeNum[min_i]; i++)
  {
   int b = vec[min_i][i].to;
   int w = vec[min_i][i].w;
   if (!vis[b] && dis[b] > dis[min_i] + w)
   {
    dis[b] = dis[min_i] + w;
    q.push(qnode(b, dis[b]));
   }
  }
 }
}

废话

以上是我对Dijkstra的一些个人理解，因为一开始学这个算法的时候看得还挺吃力，有些c++的代码还要现学…边看别人的博客边敲的代码里有很多注解，有些太傻了就没贴上去了…如果我的理解有误或者代码有问题，欢迎指出(๑•̀ㅂ•́)و✧希望能和大家好好交流学习