梯度下降与反向传播
梯度下降算法
基于梯度的优化是优化一个函数的最终取值。输入参数** ω \omega ω**,需要优化的函数是 J ( ω ) J(\omega) J(ω),基于梯度的优化即通过改变 ω \omega ω使得最大化或最小化 J ( ω ) J(\omega) J(ω),称 J ( ω ) J(\omega) J(ω)为目标函数。
对于一元函数 l = J ( ω ) l=J(\omega) l=J(ω),它的导数记为 J ′ ( ω ) J'(\omega) J′(ω),输入 w w w发生微小变化 σ \sigma σ时,输出也发生变化,可以近似为
J ( w + σ ) ≈ J ( w ) + σ J ′ ( w ) J(w+\sigma)\approx J(w) + \sigma J'(w) J(w+σ)≈J(w)+σJ′(w)
假设存在的 σ \sigma σ足够小,则有 J ( w − σ ∗ s i g n ( J ′ ( w ) ) ) < J ( w ) J(w-\sigma *sign(J'(w)))<J(w) J(w−σ∗sign(J′(w)))<J(w),其中 s i g n sign sign是符号函数。当 J ′ ( w ) J'(w) J′(w)小于0时,随着 w w w增加, J ( w ) J(w) J(w)减小,而当 J ′ ( w ) J'(w) J′(w)大于0时,随着 w w w减小, J ( w ) J(w) J(w)才能减小。 w w w的变化方向(+或者-)与导数 J ( w ) J(w) J(w)的方向(正负)相反。
多元函数:方向导数与梯度的理解,参考博客https://www.cnblogs.com/wangguchangqing/p/10521330.html#autoid-0-0-0
方向导数
方向导数是指 z = f ( x , y ) z=f(x,y) z=f(x,y)在某一点 P P P沿着某个方向 l l l的变化率,是一个数值。记为
∂ f ∂ l = l i m ρ → 0 f ( x + Δ x , y + Δ y ) − f ( x , y ) ρ \frac {\partial f}{\partial l}={lim}_{\rho \to 0} \frac{f(x+\Delta x,y+\Delta y)-f(x,y)} {\rho} ∂l∂f=limρ→0ρf(x+Δx,y+Δy)−f(x,y)
自点 P P P引射线 l l l,与 X X X正轴方向的夹角为 θ \theta θ,与函数 z = f ( x , y ) z=f(x,y) z=f(x,y)的交点 P ′ ( x + Δ x , y + Δ y ) P'(x+\Delta x,y+\Delta y) P′(x+Δx,y+Δy),函数在 P 、 P ′ P、P' P、P′的增量为 f ( x + Δ x , y + Δ y ) − f ( x , y ) f(x+\Delta x,y+\Delta y)-f(x,y) f(x+Δx,y+Δy)−f(x,y),两点之间的距离 ρ = ( Δ x ) 2 + ( Δ y ) 2 \rho = \sqrt {(\Delta x) ^2+ (\Delta y)^2} ρ=(Δx)2+(Δy)2。若 P ′ P' P′沿着 l l l趋近于 P P P,如果增量与距离比值的极限存在,称该值为函数在 P P P处的方向导数,即公式(2)。
同时,若函数在 P P P处可微,则有 f ( x + Δ x , y + Δ y ) − f ( x , y ) = ∂ f ∂ x ⋅ Δ x + ∂ f ∂ y ⋅ Δ y + o ( ρ ) f(x+\Delta x,y+\Delta y)-f(x,y)= \frac {\partial f} {\partial x}\cdot \Delta x +\frac {\partial f} {\partial y} \cdot \Delta y+o(\rho) f(x+Δx,y+Δy)−f(x,y)=∂x∂f⋅Δx+∂y∂f⋅Δy+o(ρ),
两边同除以 ρ \rho ρ,可以得到
f ( x + Δ x , y + Δ y ) − f ( x , y ) ρ = ∂ f ∂ x ⋅ cos θ + ∂ f ∂ y ⋅ sin θ + o ( ρ ) ρ \frac{f(x+\Delta x,y+\Delta y)-f(x,y)} {\rho}= \frac {\partial f} {\partial x}\cdot\cos \theta +\frac {\partial f} {\partial y}\cdot \sin \theta + \frac {o(\rho)} {\rho} ρf(x+Δx,y+Δy)−f(x,y)=∂x∂f⋅cosθ+∂y∂f⋅sinθ+ρo(ρ)
取极限得到
∂ f ∂ l = l i m ρ → 0 f ( x + Δ x , y + Δ y ) − f ( x , y ) ρ = f x ⋅ cos θ + f y ⋅ sin θ \frac {\partial f}{\partial l}={lim}_{\rho \to 0} \frac{f(x+\Delta x,y+\Delta y)-f(x,y)} {\rho} =f_x \cdot \cos \theta +f_y \cdot \sin \theta ∂l∂f=limρ→0ρf(x+Δx,y+Δy)−f(x,y)=fx⋅cosθ+fy⋅sinθ
梯度
梯度是指是这样一个向量:每个元素为函数对一元变量的偏导数,它的大小即为最大方向导数。梯度记为
∇ f = g r a d f ( x , y ) = ∂ f ∂ x ⋅ i + ∂ f ∂ y ⋅ j \nabla f = gradf(x,y)= \frac {\partial f} {\partial x}\cdot i + \frac {\partial f} {\partial y}\cdot j ∇f=gradf(x,y)=∂x∂f⋅i+∂y∂f⋅j
梯度与方向导数的联系:
设向量 e = cos θ ∗ i + sin θ ∗ j e=\cos \theta *i +\sin \theta*j e=cosθ∗i+sinθ∗j与 l l l同方向,根据方向导数的计算公式,有
∂ f ∂ l = ∂ f ∂ x cos θ + ∂ f ∂ y sin θ = [ ∂ f ∂ x ∂ f ∂ y ] [ cos θ sin θ ] = ∇ f ⋅ e = ∣ ∣ ∇ f ∣ ∣ cos < ∇ f , e > \frac {\partial f}{\partial l} =\frac {\partial f} {\partial x}\cos \theta +\frac {\partial f} {\partial y}\sin \theta = \begin{bmatrix} \frac {\partial f} {\partial x} & \frac {\partial f} {\partial y}\end{bmatrix} \begin{bmatrix} \cos \theta \\ \sin \theta \end{bmatrix} = \nabla f \cdot e =||\nabla f|| \cos<\nabla f,e> ∂l∂f=∂x∂fcosθ+∂y∂fsinθ=[∂x∂f∂y∂f][cosθsinθ]=∇f⋅e=∣∣∇f∣∣cos<∇f,e>
其中 cos < ∇ f , e > \cos<\nabla f,e> cos<∇f,e>表示梯度 ∇ f \nabla f ∇f与向量的夹角, ∣ ∣ ∇ f ∣ ∣ ||\nabla f|| ∣∣∇f∣∣表示梯度的大小。可以看到,当方向向量与梯度同方向时,方向导数达到最大值,且最大值等于梯度的大小。
最大方向导数的等于梯度的模, ∣ ∣ ∇ f ∣ ∣ = f x 2 + f y 2 ||\nabla f||=\sqrt{f_x^2+f_y^2} ∣∣∇f∣∣=fx2+fy2,而梯度的方向由梯度向量与 X X X轴的角度给出, α ( x , y ) = arctan f y f x \alpha(x,y)=\arctan \frac {f_y}{f_x} α(x,y)=arctanfxfy
由上述可得,函数在某点沿着梯度的方向增长最快,逆梯度方向减小最快。因此,要想求得函数的极小值(或最小值),可以通过沿逆梯度方向变化,不断下降找到极小值。
e g : eg: eg:
函数 J ( θ ) = 2 − 3 θ 1 + 4 θ 2 − 5 θ 3 J(\theta) = 2-3\theta_1+4\theta_2 -5\theta_3 J(θ)=2−3θ1+4θ2−5θ3,则梯度为
∇ J ( θ ) = [ ∂ J ∂ θ 1 ∂ J ∂ θ 2 ∂ J ∂ θ 3 ] = [ − 3 4 − 5 ] \nabla J(\theta)=\begin{bmatrix} \frac {\partial J} {\partial \theta_1} & \frac {\partial J} {\partial \theta_2} & \frac {\partial J} {\partial \theta_3}\end{bmatrix} =\begin{bmatrix}-3 &4 & -5 \end{bmatrix} ∇J(θ)=[∂θ1∂J∂θ2∂J∂θ3∂J]=[−34−5]
梯度下降算法步骤
算法步骤:
给定目标函数 f ( x ) f(x) f(x)和初始点位置 x 0 x_0 x0
- 计算梯度,取反表示沿逆梯度方向。 Δ x t = − ∇ f ( x t ) \Delta x_t=-\nabla f(x_t) Δxt=−∇f(xt)
- 计算下一处的值:每次参数移动的幅度是 σ \sigma σ,称为学习率。更新后的参数 x t + 1 = x t + σ ⋅ Δ x t x_{t+1}=x_t+\sigma \cdot\Delta x_t xt+1=xt+σ⋅Δxt
- 重复1、2,直至 ∣ Δ x t ∣ < ϵ |\Delta x_t| <\epsilon ∣Δxt∣<ϵ ,其中 ϵ \epsilon ϵ是预先设置一个很小的值,满足条件时结束。
e g : eg: eg:
函数 J ( w ) = w 2 J(w)=w^2 J(w)=w2,它的梯度计算公式为 ∇ = 2 ⋅ w \nabla = 2\cdot w ∇=2⋅w初始位置 w = 10 w=10 w=10,使用梯度下降计算极小值。其中学习率0.2。
计算过程如下
| 轮数 | 当前参数值 w w w | 梯度取反 Δ w t = − 2 w \Delta w_t=-2w Δwt=−2w | 更新后的参数值 w t + σ ⋅ Δ w t w_t+\sigma \cdot \Delta w_t wt+σ⋅Δwt |
|---|---|---|---|
| 1 | 10 | -20 | 6.0 |
| 2 | 6.0 | -12.0 | 3.6 |
| 3 | 3.6 | -7.2 | 2.16 |
| 4 | 2.16 | -4.32 | 1.296 |
| 5 | 1.296 | -2.592 | 0.7776 |
| 6 | 0.7776 | -1.5552 | 0.466560 |
| 7 | 0.466560 | -0.933120 | 0.279936 |
| 8 | 0.279936 | -0.559872 | 0.167962 |
| 9 | 0.167962 | -0.335923 | 0.100777 |
| 10 | 0.100777 | -0.201554 | 0.060466 |
几种梯度下降算法
批梯度下降 batch gradient descent (BGD)
在每次参数更新时使用全部的样本数据, θ i = θ i − α ∑ j = 0 m ( h θ ( x 0 ( j ) , x 1 ( j ) , . . . x n ( j ) ) − y j ) x i ( j ) \theta_i = \theta_i - \alpha\sum\limits_{j=0}^{m}(h_\theta(x_0^{(j)}, x_1^{(j)}, ...x_n^{(j)}) - y_j)x_i^{(j)} θi=θi−αj=0∑m(hθ(x0(j),x1(j),...xn(j))−yj)xi(j),优点是充分利用了全部数据,保证在足够多的的迭代后可以达到最优,缺点是数据量过大时迭代十分缓慢,收敛速度很慢。
随机梯度下降 stochastic gradient descent (SGD)
与BGD不同在于,每次使用一个样本用于更新参数。 θ i = θ i − α ( h θ ( x 0 ( j ) , x 1 ( j ) , . . . x n ( j ) ) − y j ) x i ( j ) \theta_i = \theta_i - \alpha (h_\theta(x_0^{(j)}, x_1^{(j)}, ...x_n^{(j)}) - y_j)x_i^{(j)} θi=θi−α(hθ(x0(j),x1(j),...xn(j))−yj)xi(j)。优点是一次训练一个样本速度快,但一个样本决定梯度方向, 可能导致解不是最优,而且每次样本方向变化大,不容易很快收敛到最优解或局部最优解。
小批量梯度算法 Mini-batch gradient descent
每次使用一部分样本用于更新参数,即batch_size。对一个总样本数据m的数据集,每次使用x个样本,更新公式为 θ i = θ i − α ∑ j = t t + x − 1 ( h θ ( x 0 ( j ) , x 1 ( j ) , . . . x n ( j ) ) − y j ) x i ( j ) \theta_i = \theta_i - \alpha \sum\limits_{j=t}^{t+x-1}(h_\theta(x_0^{(j)}, x_1^{(j)}, ...x_n^{(j)}) - y_j)x_i^{(j)} θi=θi−αj=t∑t+x−1(hθ(x0(j),x1(j),...xn(j))−yj)xi(j)
batch_size=1时,即为SGD的情况,batch_size=m时,即为BGD的情况。
梯度下降的缺陷
图片出自《深度学习与计算机视觉、算法原理、框架与代码实现》
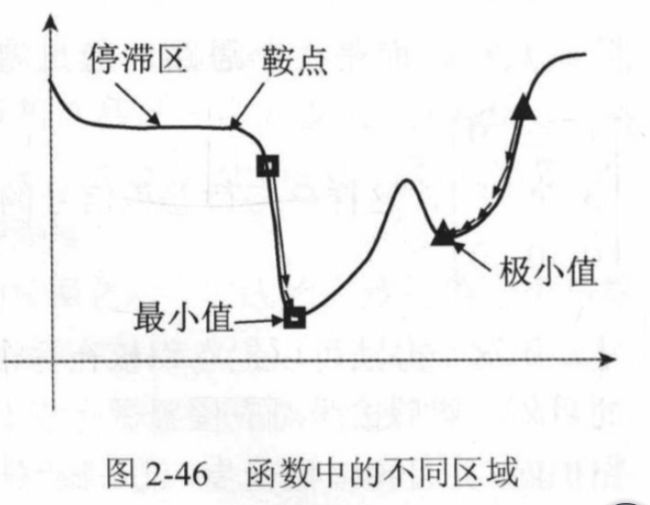
函数的特殊点。从梯度下降的步骤来看,根据梯度的方向判断参数移动的方向,但是当 J ′ ( w ) = 0 J'(w)=0 J′(w)=0的时候,就无法判断往哪边移动。称 J ′ ( w ) = 0 J'(w)=0 J′(w)=0的点为驻点或者临界点。
函数会出现存在梯度为0的临界点,但该点不是最小点也不是最大点,这种临界点称为鞍点(Saddle Point)。
函数在某一段区域,梯度很小,且范围很大,梯度值小于更新条件,此时算法可能会停止迭代,这种区域称为停滞区。
极小值的存在,也会使算法停止迭代,从而得到不准确的结果,陷入局部最优解的情况。
因此,梯度下降算法的缺陷在于鞍点、停滞区、极小值的存在。
梯度下降算法通常适用于凸函数的情况。
梯度下降算法的改进
冲量momentum
算法步骤:
给定目标函数 f ( x ) f(x) f(x)和初始点位置 x 0 x_0 x0
- 计算梯度,取反表示沿逆梯度方向。 Δ x t = − ∇ f ( x t ) \Delta x_t=-\nabla f(x_t) Δxt=−∇f(xt)
- 计算下一处的值:设置一个冲量项, V t + 1 = γ v t + η Δ x t V_{t+1}=\gamma v_t + \eta \Delta x_t Vt+1=γvt+ηΔxt,更新后的参数为 x t + 1 = x t + v t + 1 x_{t+1}=x_t+v_{t+1} xt+1=xt+vt+1
- 重复1、2。
与原始梯度下降算法不一样的是,更新参数时,考虑到一个冲量,且冲量每次迭代时要乘以衰减数。在冲量项的影响下,算法迭代就相当于带上了“惯性”,前次迭代位置前进的方向可以影响到下一次迭代。这样当算法经过鞍点或是停滞区时,就不至于停下来做过于缓慢的迭代,而经过并不是很“深”的极值时,就可以借助冲量项带来的“惯性”冲出极值所的“坑”
算法停止的的标准也不再是梯度小于一个阈值。停止算法的标准可以是冲量小于某个值,梯度小于某个值,或是用户给定一个次数就停止。
Nesterov Accelerated Gradient Descent (NAG方法)
与加入冲量的改进唯一不同是,计算梯度的位置,不是当前位置 x t x_t xt,而是沿当前冲量前进一步的位置。
给定目标函数 f ( x ) f(x) f(x)和初始点位置 x 0 x_0 x0,以及初始动量 v 0 v_0 v0
- 计算梯度,取反表示沿逆梯度方向。 Δ x t = − ∇ f ( x t + γ v t ) \Delta x_t=-\nabla f(x_t+\gamma v_t) Δxt=−∇f(xt+γvt)
- 计算下一处的值:设置一个冲量项, V t + 1 = γ v t + η Δ x t V_{t+1}=\gamma v_t + \eta \Delta x_t Vt+1=γvt+ηΔxt,更新后的参数为 x t + 1 = x t + v t + 1 x_{t+1}=x_t+v_{t+1} xt+1=xt+vt+1
- 重复1、2。
反向传播算法( BackPropagation算法 BP)
此部分参考了一篇博客,https://www.cnblogs.com/charlotte77/p/5629865.html,
写的超级详细,跟着走了一遍过程,很容易理解反向传播的计算过程。
此外,参考《机器学习》的BP算法步骤,总结很简练,但没有具体数据去实现,看着很抽象。
算法的主要思想:
- 数据集输入神经网络,经过隐藏层,最终达到输出层。该过程是前向传播过程。
- 计算输出结果与真实结果存在误差,因此计算出误差,并将该误差从输出层向隐藏层反向传播,直至传播到输入层。
- 在反向传播的过程中,根据误差调整各种参数的值;不断迭代上述过程,直至收敛
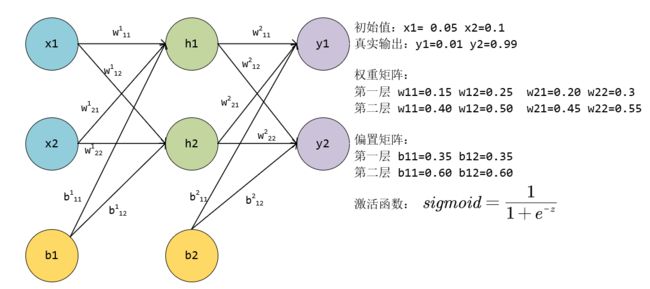
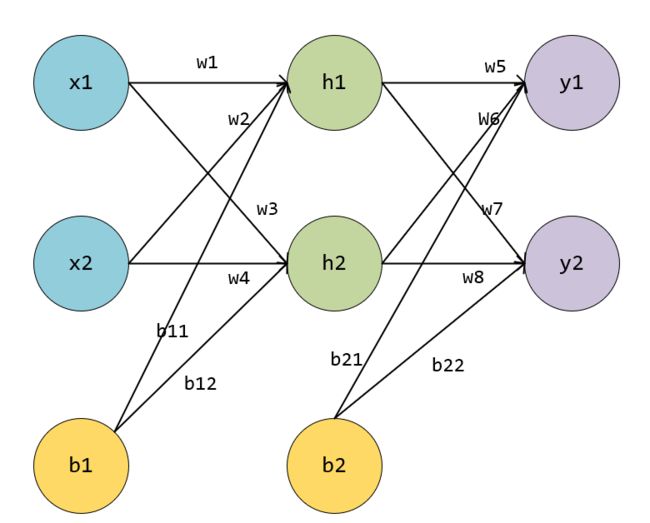
e g : eg: eg: 以下图为例,使用BP算法更新各层参数。
-
输入 ( 0.05 , 0.1 ) (0.05,0.1) (0.05,0.1) 计算各级的输出:
隐藏层输入 h 1 i n = w 11 1 ∗ x 1 + w 21 1 ∗ x 2 + b 11 1 = 0.15 ∗ 0.05 + 0.2 ∗ 0.1 + 0.35 = 0.3775 h1_{in}=w_{11}^1*x_1 +w_{21}^1*x_2+b_{11}^1=0.15*0.05+0.2*0.1+0.35=0.3775 h1in=w111∗x1+w211∗x2+b111=0.15∗0.05+0.2∗0.1+0.35=0.3775
输入 h 2 i n = w 12 1 ∗ x 1 + w 22 1 ∗ x 2 + b 12 1 = 0.25 ∗ 0.05 + 0.3 ∗ 0.1 + 0.35 = 0.3925 h2_{in}=w_{12}^1*x_1 +w_{22}^1*x_2+b_{12}^1=0.25*0.05+0.3*0.1+0.35=0.3925 h2in=w121∗x1+w221∗x2+b121=0.25∗0.05+0.3∗0.1+0.35=0.3925
隐藏层输出: h 1 o u t = s i g m o i d ( h 1 i n ) = 0.59326999211 h1_{out}=sigmoid(h1_{in})=0.59326999211 h1out=sigmoid(h1in)=0.59326999211 h 2 o u t = s i g m o i d ( h 2 i n ) = 0.596884378259767 h2_{out}=sigmoid(h2_{in})=0.596884378259767 h2out=sigmoid(h2in)=0.596884378259767
隐藏层到输出层:
神经元 y 1 y_1 y1的输入输出是[1.10590596705977 0.7513650695523157]
神经元 y 2 y_2 y2的输入输出是[1.2249214040964653 0.7729284653214625]
因此,前向传播的输出结果是 [ 0.7513650695523157 0.7729284653214625 ] \begin{bmatrix} 0.7513650695523157 & 0.7729284653214625 \end{bmatrix} [0.75136506955231570.7729284653214625] 而真实值是 [ 0.01 0.99 ] \begin{bmatrix} 0.01 & 0.99 \end{bmatrix} [0.010.99]
-
计算前向传播的结果与真实值的误差 ,使用均方误差
E k = 1 2 ∑ i ( y p r e d i c t − y t r u t h ) 2 E_k = \frac 1 2 \sum_i (y_{predict}-y_{truth}) ^2 Ek=21i∑(ypredict−ytruth)2
根据公式,可以算出总误差值 E k = 1 2 ( ( 0.7513650695523157 − 0.01 ) 2 + ( 0.7729284653214625 − 0.99 ) 2 ) = 0.2983711087600027 E_k = \frac 1 2 ((0.7513650695523157-0.01)^2+(0.7729284653214625-0.99)^2)=0.2983711087600027 Ek=21((0.7513650695523157−0.01)2+(0.7729284653214625−0.99)2)=0.2983711087600027
-
反向传播,更新参数。
误差的公式
M S E = 1 2 [ ( y 1 o u t − y 1 t r u t h ) 2 + ( y 2 o u t − y 2 t r u t h ) 2 ] 其 中 y 1 t r u t h 、 y 2 t r u t h 都 是 常 量 MSE = \frac 1 2 [(y1_{out}-y1_{truth})^2+(y2_{out}-y2_{truth})^2] 其中y1_{truth}、y2_{truth}都是常量 MSE=21[(y1out−y1truth)2+(y2out−y2truth)2]其中y1truth、y2truth都是常量误差公式中只有输出值是变量,每个输出值又是通过各个路径的参数“复合”而来,看成一个复合函数。以输出y1为例: y 1 o u t = s i g m o i d ( y 1 i n ) = s i g m o i d ( h 1 o u t ∗ w 5 + h 2 o u t ∗ w 6 + b 21 ) y1_{out} = sigmoid(y1_{in})=sigmoid(h1_{out}*w_5+h2_{out}*w_6+b21) y1out=sigmoid(y1in)=sigmoid(h1out∗w5+h2out∗w6+b21),而 h 1 o u t 、 h 2 o u t h1_{out}、h2_{out} h1out、h2out等又可以推向输出层。 h 1 o u t = s i g m o i d ( h 1 i n ) = s i g m o i d ( x 1 ∗ w 1 + x 2 ∗ w 2 + b 11 ) h1_{out}=sigmoid(h1_{in})=sigmoid(x_1*w1+x2*w2+b_{11}) h1out=sigmoid(h1in)=sigmoid(x1∗w1+x2∗w2+b11)
故
y 1 o u t = s i g m o i d ( y 1 i n ) = s i g m o i d ( h 1 o u t ∗ w 5 + h 2 o u t ∗ w 6 + b 21 ) = s i g m o i d ( s i g m o i d ( h 1 i n ) ∗ w 5 + s i g m o i d ( h 2 i n ) ∗ w 6 + b 21 ) = s i g m o i d ( s i g m o i d ( x 1 ∗ w 1 + x 2 ∗ w 2 + b 11 ) ∗ w 5 + s i g m o i d ( x 1 ∗ w 3 + x 2 ∗ w 4 + b 12 ) + b 21 ) y1_{out} = sigmoid(y1_{in})=sigmoid(h1_{out}*w_5+h2_{out}*w_6+b_{21})\\=sigmoid(sigmoid(h1_{in})*w5+sigmoid(h2_{in})*w_6+b_{21})\\ =sigmoid(sigmoid(x_1*w1+x2*w2+b_{11})*w_5+sigmoid(x_1*w_3+x_2*w_4+b_{12})+b_{21}) y1out=sigmoid(y1in)=sigmoid(h1out∗w5+h2out∗w6+b21)=sigmoid(sigmoid(h1in)∗w5+sigmoid(h2in)∗w6+b21)=sigmoid(sigmoid(x1∗w1+x2∗w2+b11)∗w5+sigmoid(x1∗w3+x2∗w4+b12)+b21)计算误差与某个参数 w w w的偏导,使用链式法则求偏导。
从输出层到隐藏层的参数
例如计算 w 5 w_5 w5对最终损失的影响,偏导公式如下。没有考虑 y 2 o u t y2_{out} y2out,因为 y 2 y2 y2的传播路径与 w 5 w5 w5无关。
∂ ∂ w 5 M S E = ∂ M S E ∂ y 1 o u t ∗ ∂ y 1 o u t ∂ y 1 i n ∗ ∂ y 1 i n ∂ w 5 \frac {\partial} {\partial w_5}MSE=\frac {\partial MSE} {\partial y1_{out}}*\frac {\partial y1_{out}} {\partial y1_{in}}*\frac {\partial y1_{in}} {\partial w_5} ∂w5∂MSE=∂y1out∂MSE∗∂y1in∂y1out∗∂w5∂y1in依次计算该公式的各个部分的值。
M S E MSE MSE对 y 1 o u t y1_{out} y1out的偏导,
∂ M S E ∂ y 1 o u t = ∂ 1 2 [ ( y 1 o u t − y 1 t r u t h ) 2 + ( y 2 o u t − y 2 t r u t h ) 2 ] ∂ y 1 o u t = y 1 o u t − y 1 t r u t h = 0.74136507 \frac {\partial MSE} {\partial y1_{out}}=\frac {\partial\frac 1 2 [(y1_{out}-y1_{truth})^2+(y2_{out}-y2_{truth})^2] } {\partial y1_{out}}=y1_{out}-y1_{truth}=0.74136507 ∂y1out∂MSE=∂y1out∂21[(y1out−y1truth)2+(y2out−y2truth)2]=y1out−y1truth=0.74136507y 1 o u t y1_{out} y1out对 y 1 i n y1_{in} y1in的偏导,sigmoid函数的导数公式是 f ′ ( x ) = f ( x ) ∗ ( 1 − f ( x ) ) f'(x)=f(x)*(1-f(x)) f′(x)=f(x)∗(1−f(x))。
根据计算式 y 1 o u t = s i g m o i d ( y 1 i n ) y1_{out}=sigmoid(y1_{in}) y1out=sigmoid(y1in)可以算出
∂ y 1 o u t ∂ y 1 i n = y 1 o u t ∗ ( 1 − y 1 o u t ) = 0.75136507 ∗ ( 1 − 0.75136507 ) = 0.1868156016 \frac {\partial y1_{out}} {\partial y1_{in}}=y1_{out}*(1-y1_{out})=0.75136507*(1-0.75136507)=0.1868156016 ∂y1in∂y1out=y1out∗(1−y1out)=0.75136507∗(1−0.75136507)=0.1868156016
y 1 i n y1_{in} y1in对 w 5 w_5 w5的偏导,计算式 y 1 i n = h 1 o u t ∗ w 5 + h 2 o u t ∗ w 6 + b 21 y1_{in}=h1_{out}*w_5+h2_{out}*w_6+b_{21} y1in=h1out∗w5+h2out∗w6+b21,可以算出
∂ y 1 i n ∂ w 5 = h 1 o u t = 0.59326999211 \frac {\partial y1_{in}} {\partial w_5}=h1_{out}=0.59326999211 ∂w5∂y1in=h1out=0.59326999211
最后将三者乘起来,得到
∂ ∂ w 5 M S E = 0.74136507 ∗ 0.1868156016 ∗ 0.59326999211 = 0.08216704052233154 \frac {\partial} {\partial w_5}MSE =0.74136507*0.1868156016*0.59326999211=0.08216704052233154 ∂w5∂MSE=0.74136507∗0.1868156016∗0.59326999211=0.08216704052233154
更新 w 5 w_5 w5的值, w 5 = w 5 − σ ∗ ∂ ∂ w 5 M S E = 0.4 − 0.5 ∗ 0.08216704052233154 = 0.3589164797388342 w_5=w_5 - \sigma * \frac {\partial} {\partial w_5}MSE=0.4-0.5*0.08216704052233154=0.3589164797388342 w5=w5−σ∗∂w5∂MSE=0.4−0.5∗0.08216704052233154=0.3589164797388342其中 σ \sigma σ是学习率,更新公式和梯度下降算法一样。
总误差对 w 5 w_5 w5的偏导: ( y 1 o u t − y 1 t r u t h ) ∗ [ y 1 o u t ∗ ( 1 − y 1 o u t ) ] ∗ h 1 o u t (y1_{out}-y1_{truth})*[y1_{out}*(1-y1_{out})]*h1_{out} (y1out−y1truth)∗[y1out∗(1−y1out)]∗h1out
同理可得对 w 6 、 w 7 、 w 8 w_6、w_7、w_8 w6、w7、w8的偏导。
∂ ∂ w 6 M S E = ( y 1 o u t − y 1 t r u t h ) ∗ [ y 1 o u t ∗ ( 1 − y 1 o u t ) ] ∗ h 2 o u t = 0.0826676278049868 ∂ ∂ w 7 M S E = ( y 2 o u t − y 2 t r u t h ) ∗ [ y 2 o u t ∗ ( 1 − y 2 o u t ) ] ∗ h 1 o u t = − 0.02260254047747507 ∂ ∂ w 8 M S E = ( y 2 o u t − y 2 t r u t h ) ∗ [ y 2 o u t ∗ ( 1 − y 2 o u t ) ] ∗ h 2 o u t = − 0.022740242215978222 \frac {\partial} {\partial w_6}MSE =(y1_{out}-y1_{truth})*[y1_{out}*(1-y1_{out})]*h2_{out}=0.0826676278049868\\ \frac {\partial} {\partial w_7}MSE =(y2_{out}-y2_{truth})*[y2_{out}*(1-y2_{out})]*h1_{out}=-0.02260254047747507\\ \frac {\partial} {\partial w_8}MSE =(y2_{out}-y2_{truth})*[y2_{out}*(1-y2_{out})]*h2_{out}=-0.022740242215978222 ∂w6∂MSE=(y1out−y1truth)∗[y1out∗(1−y1out)]∗h2out=0.0826676278049868∂w7∂MSE=(y2out−y2truth)∗[y2out∗(1−y2out)]∗h1out=−0.02260254047747507∂w8∂MSE=(y2out−y2truth)∗[y2out∗(1−y2out)]∗h2out=−0.022740242215978222
更新后的参数
w 6 = w 6 − σ ∗ ∂ ∂ w 6 M S E = 0.4086661860975066 w 7 = w 7 − σ ∗ ∂ ∂ w 7 M S E = 0.5113012702387375 w_6 = w_6 - \sigma * \frac {\partial} {\partial w_6}MSE=0.4086661860975066\\ w_7 = w_7 - \sigma * \frac {\partial} {\partial w_7}MSE=0.5113012702387375 w6=w6−σ∗∂w6∂MSE=0.4086661860975066w7=w7−σ∗∂w7∂MSE=0.5113012702387375
偏置更新: y 1 o u t = s i g m o i d ( y 1 i n ) y1_{out}=sigmoid(y1_{in}) y1out=sigmoid(y1in), y 1 i n y1_{in} y1in中的偏置项只有一项,偏导是1。因此复合后的结果是 ∂ ∂ b 21 M S E = y 1 o u t ∗ ( y 1 o u t − y 1 o u t ) \frac {\partial} {\partial b_{21}}MSE =y1_{out}*(y1_{out}-y1_{out}) ∂b21∂MSE=y1out∗(y1out−y1out)
b 21 = b 21 − σ ∗ [ y 1 o u t ∗ ( 1 − y 1 o u t ) ] = 0.6 − 0.5 ∗ 0.1868156016 = 0.5065921992 b 22 = b 22 − σ ∗ [ y 2 o u t ∗ ( 1 − y 2 o u t ) ] = 0.6 − 0.5 ∗ 0.1755100528 = 0.5122449736 b_{21}=b_{21}- \sigma * [y1_{out}*(1-y1_{out})] = 0.6-0.5*0.1868156016=0.5065921992\\ b_{22}=b_{22}- \sigma * [y2_{out}*(1-y2_{out})] = 0.6-0.5*0.1755100528=0.5122449736 b21=b21−σ∗[y1out∗(1−y1out)]=0.6−0.5∗0.1868156016=0.5065921992b22=b22−σ∗[y2out∗(1−y2out)]=0.6−0.5∗0.1755100528=0.5122449736
从隐藏层到输入层的参数更新
以 w 1 w_1 w1为例,但是与上面不同的是, w 1 w_1 w1会影响到全部的输出,因为它通过 h 1 、 w 5 、 w 7 h_1、w_5、w_7 h1、w5、w7传播到两个输出y,因此会有两个误差。(这段公式老是报错。。。只好贴图了)
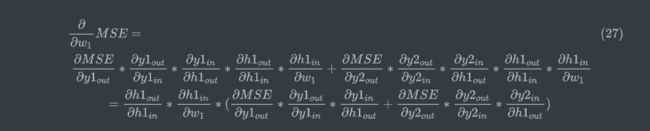
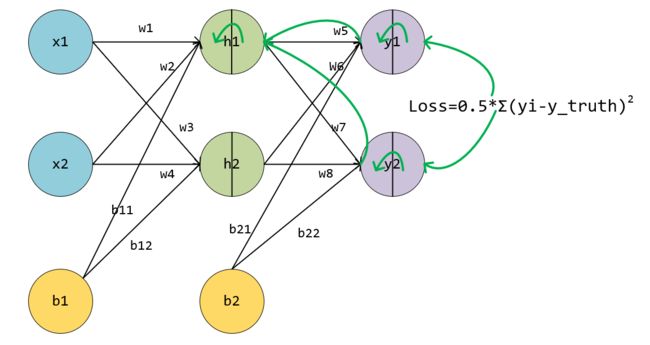
如上图绿色箭头,每个神经元被分为两块,左边表示输入in,右边表示输出out,绿色表示反向传播的路径,截止到w1,可以看到,损失对w1的偏导,分为两条路径,但两条路径有部分是共用,即 h 1 o u t h1_{out} h1out反向传播到输入层的部分。
公式(19)的计算过程如下,可以发现部分运算值已经在上面的w5到w8部分更新过一次。
∂ M S E ∂ y 1 o u t ∗ ∂ y 1 o u t ∂ y 1 i n = [ ∂ 1 2 [ ( y 1 o u t − y 1 t r u t h ) 2 + ( y 2 o u t − y 2 t r u t h ) 2 ] ∂ y 1 o u t ] [ y 1 o u t ∗ ( 1 − y 1 o u t ) ] = 0.74136507 ∗ [ 0.75136507 ∗ ( 1 − 0.75136507 ) ] = 0.13849856154533652 \frac {\partial MSE} {\partial y1_{out}}*\frac {\partial y1_{out}} {\partial y1_{in}}= [\frac {\partial\frac 1 2 [(y1_{out}-y1_{truth})^2+(y2_{out}-y2_{truth})^2] } {\partial y1_{out}}] [y1_{out}*(1-y1_{out})]\\=0.74136507*[0.75136507*(1-0.75136507)] =0.13849856154533652 ∂y1out∂MSE∗∂y1in∂y1out=[∂y1out∂21[(y1out−y1truth)2+(y2out−y2truth)2]][y1out∗(1−y1out)]=0.74136507∗[0.75136507∗(1−0.75136507)]=0.13849856154533652
而
∂ y 1 i n ∂ h 1 o u t = w 5 = 0.4 , 因 为 y 1 i n 是 线 性 叠 加 而 来 , 与 h 1 有 关 的 边 只 有 w 5 \frac {\partial y1_{in}} {\partial h1_{out}}=w_5=0.4,因为y1_{in}是线性叠加而来,与h1有关的边只有w_5 ∂h1out∂y1in=w5=0.4,因为y1in是线性叠加而来,与h1有关的边只有w5
同理可以算出
∂ M S E ∂ y 2 o u t ∗ ∂ y 2 o u t ∂ y 2 i n = ( y 2 o u t − y 2 t r u t h ) ∗ ( y 2 o u t ∗ ( 1 − y 2 o u t ) ) = − 0.038098236516556236 \frac {\partial MSE} {\partial y2_{out}}*\frac {\partial y2_{out}} {\partial y2_{in}}= (y2_{out}-y2_{truth})*(y2_{out}*(1-y2_{out}))=-0.038098236516556236 ∂y2out∂MSE∗∂y2in∂y2out=(y2out−y2truth)∗(y2out∗(1−y2out))=−0.038098236516556236
而
∂ y 2 i n ∂ h 1 o u t = w 7 = 0.5 , 因 为 y 2 i n 是 线 性 叠 加 而 来 , 与 h 1 有 关 的 边 只 有 w 7 \frac {\partial y2_{in}} {\partial h1_{out}}=w_7=0.5,因为y2_{in}是线性叠加而来,与h1有关的边只有w_7 ∂h1out∂y2in=w7=0.5,因为y2in是线性叠加而来,与h1有关的边只有w7
从而,公式(19)的括号里的值,计算结果是
0.13849856154533652 ∗ 0.4 − 0.038098236516556236 ∗ 0.5 = 0.03635030635985649 0.13849856154533652*0.4-0.038098236516556236*0.5=0.03635030635985649 0.13849856154533652∗0.4−0.038098236516556236∗0.5=0.03635030635985649
计算 h 1 o u t h1_{out} h1out到 w 1 w_1 w1的偏导。从 h 1 o u t h1_{out} h1out到 h 1 i n h1_{in} h1in,是一个sigmoid函数,而 h 1 i n h1_{in} h1in到输入是线性叠加,与 w 1 w_1 w1有关的项是 w 1 ∗ x 1 w1*x1 w1∗x1,因此 h 1 i n h1_{in} h1in对于 w 1 w_1 w1的偏导是 x 1 x_1 x1
∂ h 1 o u t ∂ h 1 i n ∗ ∂ h 1 i n ∂ w 1 = h 1 o u t ∗ ( 1 − h 1 o u t ) ∗ x 1 = 0.012065035428616262 \frac {\partial h1_{out}} {\partial h1_{in}}*\frac {\partial h1_{in}} {\partial w_{1}}=h1_{out}*(1-h1_{out})*x_1=0.012065035428616262 ∂h1in∂h1out∗∂w1∂h1in=h1out∗(1−h1out)∗x1=0.012065035428616262
综上, ∂ ∂ w 1 M S E = 0.012065035428616262 ∗ 0.03635030635985649 = 0.0004385677340727236 \frac {\partial} {\partial w_1}MSE=0.012065035428616262*0.03635030635985649=0.0004385677340727236 ∂w1∂MSE=0.012065035428616262∗0.03635030635985649=0.0004385677340727236
更新 w 1 w_1 w1的值, w 1 = w 1 − σ ∗ ∂ ∂ w 1 M S E = 0.14978071613296362 w_1=w_1 - \sigma*\frac {\partial} {\partial w_1}MSE=0.14978071613296362 w1=w1−σ∗∂w1∂MSE=0.14978071613296362
同理,计算对 w 2 w_2 w2的偏导。可以看到与计算 w 1 w_1 w1不同的传播路径在于隐藏层到输入层是连接到 x 2 x_2 x2这个神经元,因此
∂ ∂ w 2 M S E = h 1 o u t ∗ ( 1 − h 1 o u t ) ∗ x 2 ∗ 0.03635030635985649 = 0.0008771354681454472 \frac {\partial} {\partial w_2}MSE=h1_{out}*(1-h1_{out})*x_2*0.03635030635985649=0.0008771354681454472 ∂w2∂MSE=h1out∗(1−h1out)∗x2∗0.03635030635985649=0.0008771354681454472
更新后w2的值是 w 2 = 0.1995614322659273 w_2=0.1995614322659273 w2=0.1995614322659273
同理计算w3和w4
∂ ∂ w 3 M S E = ( ∂ M S E ∂ y 1 o u t ∗ ∂ y 1 o u t ∂ y 1 i n ∗ ∂ y 1 i n ∂ h 2 o u t + ∂ M S E ∂ y 2 o u t ∗ ∂ y 2 o u t ∂ y 2 i n ∗ ∂ y 2 i n ∂ h 2 o u t ) ∗ ∂ h 2 o u t ∂ h 2 i n ∗ ∂ h 2 i n ∂ w 3 = [ ( y 1 o u t − y 1 t r u t h ) ∗ ( y 1 o u t ∗ ( 1 − y 1 o u t ) ) ∗ w 6 + ( y 2 o u t − y 2 t r u t h ) ∗ ( y 2 o u t ∗ ( 1 − y 2 o u t ) ) ∗ w 8 ] ∗ ( h 2 o u t ∗ ( 1 − h 2 o u t ) ) ∗ x 1 = 0.0004977127352608601 \frac {\partial} {\partial w_3}MSE=(\frac {\partial MSE} {\partial y1_{out}}*\frac {\partial y1_{out}} {\partial y1_{in}}*\frac {\partial y1_{in}} {\partial h2_{out}}+ \frac {\partial MSE} {\partial y2_{out}}*\frac {\partial y2_{out}} {\partial y2_{in}}*\frac {\partial y2_{in}} {\partial h2_{out}})*\frac {\partial h2_{out}} {\partial h2_{in}}*\frac {\partial h2_{in}} {\partial w_3}\\ =[(y1_{out}-y1_{truth})*(y1_{out}*(1-y1_{out}))*w_6+(y2_{out}-y2_{truth})*(y2_{out}*(1-y2_{out}))*w8]*\\(h2_{out}*(1-h_2{out}))*x1=0.0004977127352608601 ∂w3∂MSE=(∂y1out∂MSE∗∂y1in∂y1out∗∂h2out∂y1in+∂y2out∂MSE∗∂y2in∂y2out∗∂h2out∂y2in)∗∂h2in∂h2out∗∂w3∂h2in=[(y1out−y1truth)∗(y1out∗(1−y1out))∗w6+(y2out−y2truth)∗(y2out∗(1−y2out))∗w8]∗(h2out∗(1−h2out))∗x1=0.0004977127352608601
更新后 w 3 = 0.24975114363236958 w_3=0.24975114363236958 w3=0.24975114363236958
w 4 与 w 3 w4与w3 w4与w3也只有隐藏层反向到输出的位置不同,对 w 4 的 偏 导 为 0.0009954254705217202 w_4的偏导为0.0009954254705217202 w4的偏导为0.0009954254705217202,更新后 w 4 = 0.29950228726473915 w_4=0.29950228726473915 w4=0.29950228726473915
b 11 = 0.34998903580664814 b 12 = 0.3450228726473914 b_{11}= 0.34998903580664814\\ b_{12}=0.3450228726473914 b11=0.34998903580664814b12=0.3450228726473914
全部更新一轮后的输出结果为 [ 0.7237123710461725 0.7595051820170899 ] \begin{bmatrix} 0.7237123710461725 & 0.7595051820170899 \end{bmatrix} [0.72371237104617250.7595051820170899],损失由0.29837110876000270变降低到0.2812566048506621
总结:
这部分内容,在书上都放在了神经网络的优化方法部分。神经网络的训练实际上就是通过不断的训练,通过某种算法更新网络各个层级的权重参数,从而使损失函数降低。
梯度下降是通过函数的梯度性质来求解函数最小值,当然优缺点也很明显。除了梯度下降,还有牛顿-拉普森法、Adam法等很多其他优化算法。
而反向传播算法,是针对神经网络逆向优化所有参数,利用了梯度下降计算,达到一个全局最优的解。