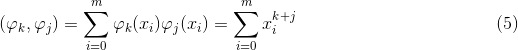数值计算—曲线拟合—最小二乘法（附源代码）

目录

最小二乘法的原理

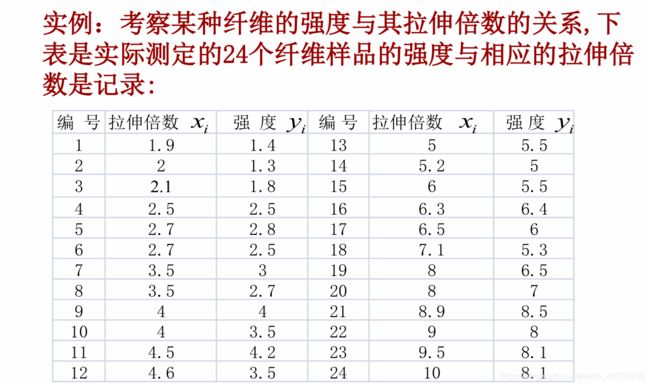
实例：

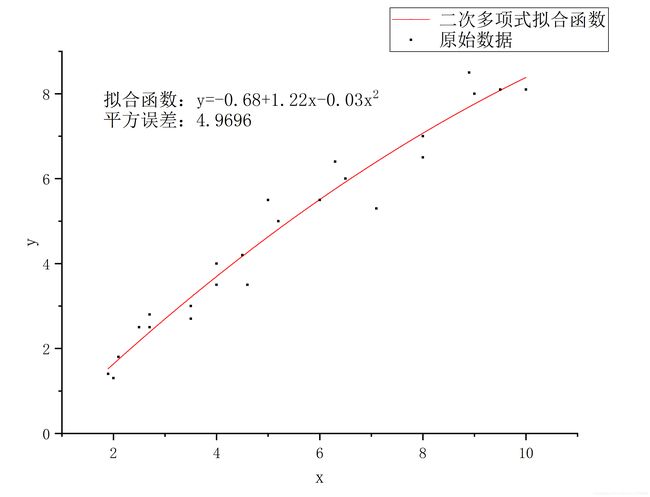
求解结果：

c++程序源代码：

---

最小二乘法的原理

拟合函数：

                                                                       

式中：s(x)为拟合函数，  为拟合系数，为函数族

平方误差：

                                             

（1）式可简化为线性方程组：

                                           

 式中：为函数序列在点上的法方程组。

多项式拟合函数S(x)的基函数为：

                                                        

基函数之间的内积为:

                                                                        

                                                                          

实例：

求解结果：

 

c++程序源代码：

//高等数值计算——曲线拟合——最小二乘法
//开发人员：chenshuai  开发日期：2019.11.20   邮箱：[email protected] 
#include "pch.h"
#include 
#include //文件输入/输出流 
#include  //参数化输入/输出 
#define n_polynomial 1  //需要拟合的多项式次数
#include 
using namespace std;
vector least_square_method(vectorx, vectory, vectora);//声明最小二乘法函数,x,y为原始数据，a为拟合多项式的系数列向量
double phi(double x, int n_cishu);  //函数族计算
vector least_square_method(vectorx, vectory, vectora)//最小二乘法函数定义
{
	int n_data=size(x),n_num = size(a);
	vector>phi_phi;
	vectorphi_f;
	phi_f.resize(n_num);
	phi_phi.resize(n_num, vector(n_num));
	for (int i = 0; i < n_num; i++)
	{
		for (int j = 0; j < n_num; j++)
		{
			for (int k = 0; k < n_data; k++)
			{
				phi_phi[i][j]= phi_phi[i][j]+phi(x[k],i)*phi(x[k], j);
			}
		}
		for (int k = 0; k < n_data; k++)
		{
			phi_f[i] = phi_f[i] + phi(x[k], i)*y[k];
		}
	}
	a = gaussian_elimination(phi_phi, phi_f);//多项式系数求解采用高斯消去法“参考我以前写的文章（含代码）”https://blog.csdn.net/weixin_41788456/article/details/102485139
	//平方误差求解
	double delta_2=0;
	for (int i = 0; i < n_data; i++)
	{
		delta_2 = delta_2 +y[i]*y[i];
	}
	for (int i = 0; i < n_num; i++)
	{
		delta_2 = delta_2 - a[i] * phi_f[i];
	}
	//系数矩阵与平方误差输出
	for (int i = 0; i < n_num; i++)
	{
		for (int j = 0; j < n_num; j++)
		{
			cout << fixed << setprecision(2) << setw(12) << phi_phi[i][j];
		}
		cout << fixed << setprecision(4) << setw(12) << phi_f[i] << endl;
	}
	cout << fixed << setprecision(4) << setw(12) << delta_2 << endl;
	return a;
}
double phi(double x, int n_cishu)  //函数族计算
{
	double y;
	y = pow(x, n_cishu);
	return y;
}
int main()
{
	vectorx_i= { 1.9,2,2.1,2.5,2.7,2.7,3.5,3.5,4,4,4.5,4.6,5,5.2,6,6.3,6.5,7.1,8,8,8.9,9,9.5,10};//原始数据
	vectory_i= { 1.4,1.3,1.8,2.5,2.8,2.5,3,2.7,4,3.5,4.2,3.5,5.5,5,5.5,6.4,6,5.3,6.5,7,8.5,8,8.1,8.1 };
	vectora(n_polynomial + 1);
	int n_data = size(x_i);
	a=least_square_method(x_i, y_i, a);//最小二乘法拟合函数调用
	cout << "多项式系数解为：" << endl;
	for (int i = 0; i < n_polynomial + 1; i++)
		cout << "a[" << i << "]=" << fixed << setprecision(2) << setw(5) << a[i] << endl;
	ofstream out("一次函数拟合函数数据.dat");
	double x,y, precision=0.01;
	for (x = x_i[0]; x <= x_i.back(); x = x + precision)
	{
		y = 0.0;
		for (int i = 0; i < n_polynomial + 1; i++)
		{
			y = y + a[i] * pow(x, i);
		}
		out << fixed << setprecision(4) << setw(12) << x << fixed << setprecision(4) << setw(12) << y << endl;
	}
	out.close();
	ofstream out1("原始数据.dat");
	for (int i = 0; i < n_data; i++)
	{
		out1 << fixed << setprecision(4) << setw(12) << x_i[i] << fixed << setprecision(4) << setw(12) << y_i[i] << endl;
	}
	out1.close();	
}