----------------siwuxie095
二分查找法
二分查找(Binary Search),也称 折半查找(Half-Interval Search),
是一种在有序数组中查找某一特定元素的搜索算法
「或称 二分搜索,折半搜索」
正如定义所示,二分查找法有一定的限制:对于有序数列,才能使用二分查找法
由此可知,排序算法在很多时候是作为其它算法的一个子过程。例如:如果使用
二分查找法,就要先使用一次排序算法,对要查找的内容进行一次排序
之所以进行这次排序,是因为处理有序数组,要比处理无序数组容易很多
具体查找过程:
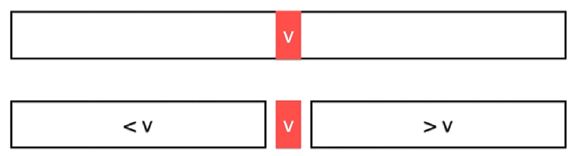
要在一个有序数组中查找某个元素,就先看这个数组的中间元素 v 与要查找的
元素,二者的大小的关系
如果中间元素 v 正好是要查找的元素,即 二者相等,非常好,直接就找到了该
元素,查找结束
否则,整个数组就被中间元素 v 分成了两部分:小于 v 的部分和大于 v 的部分
1)如果要查找的元素比 v 小,就在小于 v 的这部分继续查找即可
2)如果要查找的元素比 v 大,就在大于 v 的这部分继续查找即可
「前提:整个数组是有序的」
不难想象,整个查找过程,感觉上构造出了一棵树,即 是一个树形问题,
整个二分查找法的时间复杂度是 lgn 级别的
二分查找法的思想非常简单,而且这个思想在很早的时候就被提出来了
二分查找法的思想在 1946 年提出,但有意思的是,第一个没有 bug 的
二分查找法在 1962 年提出
程序 1:迭代的二分查找法
BinarySearch.h:
#ifndef BINARYSEARCH_H #define BINARYSEARCH_H
// 用迭代的方式写二分查找法 // // 二分查找法,在有序数组arr中,查找target // 如果找到target,返回相应的索引index // 如果没有找到target,返回-1 template int binarySearch(T arr[], int n, T target) {
// 在arr[l...r]之中查找target int l = 0, r = n - 1; while (l <= r) { //l+r 都是int 型,如果过大,相加则会有溢出的风险 //int mid = (l + r)/2; //(在归并排序中也有相同的问题) // //改为如下形式即可(无bug版): int mid = l + (r - l) / 2;
if (arr[mid] == target) { return mid; }
//在arr[l...mid-1]之中查找target //或arr[mid+1...r]之中查找target if (arr[mid] > target) { r = mid - 1; } else { l = mid + 1; }
}
return -1; }
#endif |
main.cpp:
#include "BinarySearch.h" #include #include #include using namespace std;
int main() {
int n = 1000000; int* a = new int[n]; for (int i = 0; i < n; i++) { a[i] = i; }
// 测试非递归二分查找法(迭代) clock_t startTime = clock(); for (int i = 0; i < 2 * n; i++) { int v = binarySearch(a, n, i); if (i < n) { assert(v == i); } else { assert(v == -1); } } clock_t endTime = clock();
cout << "Binary Search (Without Recursion): " << double(endTime - startTime) / CLOCKS_PER_SEC << " s" << endl;
delete []a;
system("pause"); return 0; } |
运行一览:
程序 2:递归的二分查找法
BinarySearch.h:
#ifndef BINARYSEARCH_H #define BINARYSEARCH_H
template int __binarySearch(T arr[], int l, int r, T target) {
if (l > r) { return -1; }
int mid = (l + r) / 2;
if (arr[mid] == target) { return mid; } else if (arr[mid] > target) { return __binarySearch(arr, 0, mid - 1, target); } else { return __binarySearch(arr, mid + 1, r, target); } }
// 用递归的方式写二分查找法 template int binarySearch(T arr[], int n, T target) {
return __binarySearch(arr, 0, n - 1, target); }
//递归实现通常思维起来更容易,因为每一次不需要考虑全局, //只需要考虑一个子问题 // //想好它们的递归关系,想清楚在最基础的层面是怎么做的, //就能写出这个函数来,不过递归也存在一些缺点:相比于 //迭代,递归在性能上会略差(这种差异是常数级的) // //不管是递归还是迭代,二分查找法的时间算法复杂度都是 //O(lgn)级别的
#endif |
main.cpp:
#include "BinarySearch.h" #include #include #include using namespace std;
int main() {
int n = 1000000; int* a = new int[n]; for (int i = 0; i < n; i++) { a[i] = i; }
// 测试递归的二分查找法 clock_t startTime = clock(); for (int i = 0; i < 2 * n; i++) { int v = binarySearch(a, n, i); if (i < n) { assert(v == i); } else { assert(v == -1); } } clock_t endTime = clock();
cout << "Binary Search (Recursion): " << double(endTime - startTime) / CLOCKS_PER_SEC << " s" << endl;
delete []a;
system("pause"); return 0; } |
运行一览:
二分查找法的变种
二分查找法的变种有两个非常重要的、也是应用非常广的函数,
分别叫做 floor 和 ceil
「有的地方也叫做 lower_bound 和 upper_bound」
之前实现的二分查找法,通常都是假设数组中没有重复元素
当然,即使数组中有重复元素,对于一个排好序的数组来说,依然能找到
相应元素的索引,只不过,该元素在这个数组中可能会出现很多次,之前
实现的二分查找法并不能保证找到的这个元素的索引,具体是哪个索引
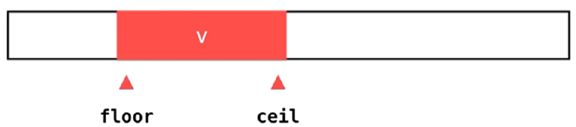
但 floor 和 ceil 这两个函数,却能保证:
1)调用 floor 来找元素 v,可以找到 v 在整个数组中第一次出现的位置
2)调用 ceil 来找元素 v,可以找到 v 在整个数组中最后一次出现的位置
这两个函数还有一个优势,即 当在数组中查找元素,如果这个元素
不存在,之前实现的二分查找法直接返回了 -1,但 floor 和 ceil 的
返回值却有所不同
具体如下:
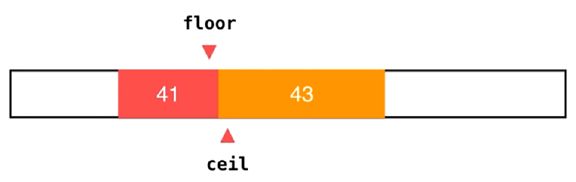
如果要在数组中查找元素 42,可以看到 42 在这个数组中并不存在,
那么 floor 返回的就是最后一个 41 的元素,而 ceil 返回的就是第一
个 43 的元素
【made by siwuxie095】