数学建模（二）

在做完第一题的数据可视化以及描述性分析后，我们接着来做第二题。
第一题链接：https://blog.csdn.net/weixin_43810148/article/details/90734226
我们重新来看一下题目：

从时间角度分析人口与经济的走势啊，读一遍题目没懂。。没关系总结一下，也就是一个时间序列分析问题，也就是分析近20年以来，重庆38个区县的经济与人口的大致走势是个什么样子。

一、GDP模型的建立
我们挑选了渝北区、大渡口区、城口县的GDP来进行分析。首先我们给出三个区县的经济走势图：

红色为渝北区的GDP随年份的走势，绿色为大渡口，蓝色为城口县。容易发现渝北区和城口县属于时间平稳序列，渝北区则属于非时间平稳序列。所以我们决定建立ARIMA模型来进行分析。但是ARIMA模型对时间序列的要求是平稳性，所以先要对渝北区进行时间序列差分，直到得到一个时间平稳序列。

差分的数学表达形式：yt’=yt-y(t-1)
即现在的时间序列值减去上一次的值。

1）差分
对渝北区GDP进行一阶差分：

可以发现折线逐渐趋于平稳。继续差分。
渝北区GDP二阶差分与三阶差分：

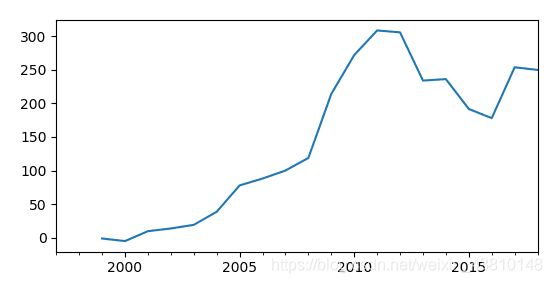
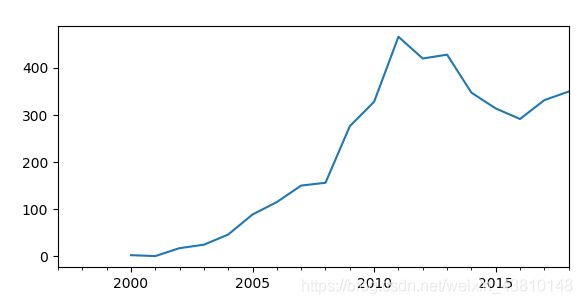
可以发现三阶差分后的时间序列与二阶差分区别不大。所以我们将模型的差分次数d=2.

2）选择最优（合适）参数

我们先来检查一下平稳时间序列的自相关图和偏自相关图：

通过两图可以观察到，自相关图有2个阶超出了置信区间。偏自相关图从第11阶开始就超出了置信区间。前十阶的偏自相关系数几乎为0。

根据上图，我们认为有以下模型可供选择：
ARIMA(0,2)模型：即自相关图在滞后2阶之后缩小为0，且偏自相关系数缩小为0。这是一个q=2的移动平均模型。
ARIMA（1,0）即偏自相关图在滞后1阶之后缩小为0，且自相关系数缩小至0，则是一个阶层p=1的自回归模型。
现在上面有两个模型可以选择，我们通常采用ARIMA模型的AIC法则。模型中有许多自由参数，增加自由参数虽然可以加大模型的拟合度，但是会容易出现过拟合的情况。AIC则会鼓励数据拟合的优良性但是尽量避免过度拟合，所以我们会优先考虑AIC值最小的那个模型。

arma_mod10 = sm.tsa.ARMA(dta,(1,0)).fit()
arma_mod02 = sm.tsa.ARMA(dta,(0,2)).fit()

print("ARIMA(1,0)的AIC是" + str(arma_mod10.aic))
print("ARIMA(0,2)的AIC是" + str(arma_mod02.aic))

ARIMA(1,0)的AIC是292.102366
ARIMA(0,2)的AIC是318.385715

可以看到ARIMA（0，1）的AIC值更小，因此ARIMA（0，1）是最佳模型。

3）模型检验
观察ARIMA（1,0）模型的残差方差是否为常数的正态分布（服从方差不变的正态分布），同时也要观察连续残差是否（自）相关。首先我们对模型做D-W检验：
DW＝O＝＞ρ＝１　　 即存在正自相关性
DW＝４＜＝＞ρ＝－１　即存在负自相关性
DW＝２＜＝＞ρ＝０　　即不存在（一阶）自相关性

arma_mod10 = sm.tsa.ARMA(dta,(1,0)).fit()
print("DW = " + str(sm.stats.durbin_watson(arma_mod10.resid.values)))

DW=0.676512
得到的DW=0.6765更接近于0，则这个模型连续残差存在正自相关性。接下来我们检验残差方差是否符合正态分布（这里我们使用QQ图）：

可以看出残差方差集中在0，服从正态分布。
根据上面两个图的结果，得到的这个模型符合我们的要求。
最后模型拟合效果如下：

总体来看拟合效果都不错。大渡口和城口县的拟合效果很好，渝北区的拟合效果相对逊色。可能是因为ARIMA模型更适用于平稳的数据序列，对于增幅较大的数据拟合效果一般。从时间角度来看，渝北区将来的GDP会越来越高，但是增长率不会大幅度改变。而大渡口区与城口县经济随时间的发展增长不明显，而且增长率会慢慢降低。

二、人口模型的建立

我们依旧拿渝北区、大渡口区和城口县的人口数量来进行分析。首先给出这三个区县的人口时间序列折线图：

通过观察，城口县和大渡口区的人口变化不大，渝北区人口虽然变化明显，但是增长速度没有发生巨大变化。我们决定使用线性回归模型来分析这3个区县的人口与时间的走势。线性回归数学表达：.y=a*x+b.

1）：确定回归系数a与回归常数b
我们根据已知的数据进行拟合（也就是监督学习），先前有一组正确数据作为训练集，经过训练后就可以建立模型。但是不是所有的点都严格按线性方程那样排布，所以我们要确定一个最优（合适）的参数去拟合它。我们抽取已知的数据点，以在坐标轴上以原点（0,0）为起点，数据点为终点做向量h(xi)=vixi。然后将已知的n个向量相加得一个新的向量：h(x)=v1x1+v2x2+…+vixi。
我们要得到这个向量的最优解，就是让计算的值与这个对应的函数值做差然后平方（求方差）。将所有已知数据做同样的操作，然后求和就能得到一个评价函数：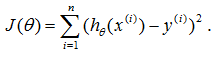
找出使这个函数最小的参数值，就能得到最佳的a,b值。

2）模型求解：
我们采用正规方程法，定义梯度为倒三角形，则评价函数的梯度为：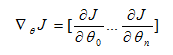
运用线性代数的知识我们知道求解梯度表示为如下形式：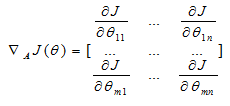
再将所有因变量写在一个矩阵中形成列向量：

我们可以得到：

进而我们得到矩阵的数学表达式：

然后对计算上面左式的梯度公式推导得到：

令导数等于0后得到：

从而可以得到的a最优值为：
得到回归系数a后，回归常数b只要代入函数即可求得。所以我们的代码主要是实现上式矩阵运算，运行的结果如下：

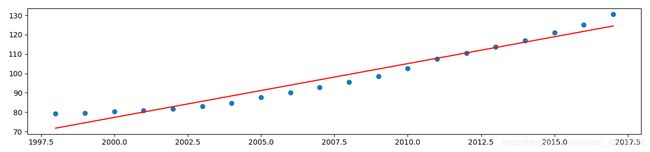
模型函数：y=2.6405x-5201.2885。 所以a=2.6405，b=-5201.2885。
同样的，我们都对大渡口区和城口县进行同上的分析，得到如下结果：

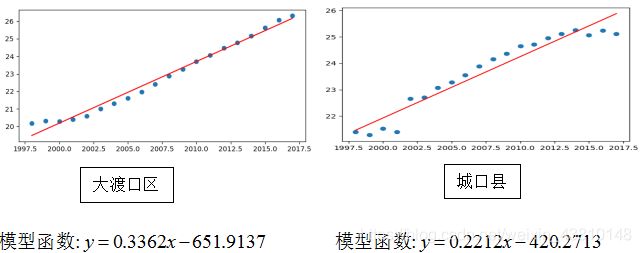
总体来看渝北区和大渡口区的拟合效果不错，但是城口县的拟合效果一般。从时间角度上看，渝北区的人口增长很快，而大渡口区也在缓慢增长。但是城口县的人口在2018年开始出现下降，所以不能保证线性回归模型适用于城口县人口数。

三、模型优化
针对城口县使用线性回归模型拟合效果一般问题，我们采用LSTM算法重新进行拟合分析。LSTM是基于RNN算法改进而来（如下图），采用深度学习，预测的值只取决于上一个训练神经元的值。这里我们只采用单变量输入。

我们考虑都数据的规模，我们在一个隐藏层中加入128个神经元。将三分之二的数据作为训练集，剩下的作为测试集。运行结果如下：

得到训练的均方根误差为0.39，测试的均方根误差为0.18。误差十分小，而且图线的拟合度也很高，可以作为城口县的人口模型。

本题代码和后面三道题的过程会在后续更新，希望大家多多关注，我是小白，如果中间有什么错误希望大家可以指出来，作为我的一个学习过程。

梯度下降法求解最优参数参考于斯坦福大学公开课。