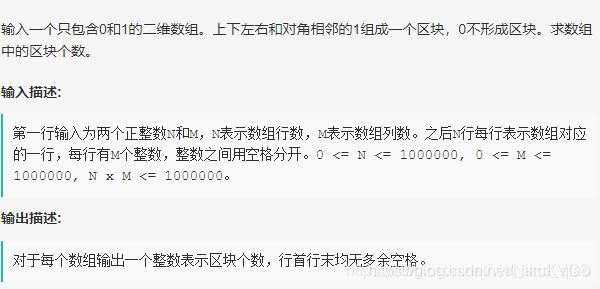
头条笔试题 广度优先搜索 深度优先搜索 算法的应用

这两个算法的用处在于，只要给定一个连通图，从连通图的任何一点开始遍历，都可以把整个连通图遍历完。

解析一道头条的笔试题

题目

案例

区块数目 ： 3

算法思路：
1.构建连通图
遍历每个节点A，添加节点A与右方和下方的连通节点的有向边。
2.dfs或者bfs遍历
对所有节点的vis状态设置为false，一旦被遍历则置为true，true的节点不可再访问
3.根据遍历的次数来获得区块数目
对所有节点顺序进行dfs或者bfs，完成一次dfs/bfs就count++

Golang实现 bfs算法思路

import (
	"fmt"
)

func seq(i, j, M int) int {
	return i*M + j
}

func main() {
	N := 0
	M := 0
	fmt.Scan(&N, &M)

	matrix := make([][]int, 0)

	for i := 0; i < N; i++ {
		temp := make([]int, 0)
		for j := 0; j < M; j++ {
			ai := 0
			fmt.Scan(&ai)
			temp = append(temp, ai)
		}
		matrix = append(matrix, temp)
	}

	graph := make([][]int, N*M)
	for i := 0; i < N; i++ {
		for j := 0; j < M; j++ {
			if matrix[i][j] == 0 {
				continue
			}
			relations := make([]int, 0)
			if j+1 < M && matrix[i][j+1] == 1 {
				relations = append(relations, seq(i, j+1, M))
			}
			if j-1 >= 0 && i+1 < N && matrix[i+1][j-1] == 1 {
				relations = append(relations, seq(i+1, j-1, M))
			}
			if i+1 < N && matrix[i+1][j] == 1 {
				relations = append(relations, seq(i+1, j, M))
			}
			if i+1 < N && j+1 < M && matrix[i+1][j+1] == 1 {
				relations = append(relations, seq(i+1, j+1, M))
			}
			graph[seq(i, j, M)] = relations
		}
	}

	vis := make([]int, N*M)
	count := 0
	for i := 0; i < len(graph); i++ {
		if matrix[i/M][i%M] == 0 || vis[i] == 1 {
			continue
		}
		bfs(i, graph, vis)
		count++
	}

	fmt.Printf("%d\n", count)

}
func bfs(i int, graph [][]int, vis []int) {
	vis[i] = 1
	if len(graph[i]) == 0 {
		return
	}
	top := 0
	queue := make([]int, 0)
	queue = append(queue, graph[i]...)
	for top < len(queue) {
		id := queue[top]
		if vis[id] == 1 {
			top++
			continue
		}
		queue = append(queue, graph[id]...)
		vis[id] = 1
		top++
	}
}

其中 bfs算法使用队列来实现，比较高效

使用python实现 dfs算法

NM = input().split()
N = int(NM[0])
M = int(NM[1])


def seq(i,j):
    return i*M + j
matrix = []

for i in range(0,N):
    val = input().split()
    row = []
    for j in range(0,M):
        row.append(int(val[j]))
    matrix.append(row)

graph = [[] for i in range(0,N*M)]


for i in range(0,N):
    for j in range(0,M):
        if 0 == matrix[i][j]:
            continue
        relations = []
        if j+1 < M and matrix[i][j+1] == 1:
            relations.append(seq(i,j+1))
        if j-1 >= 0 and i+1 < N and matrix[i+1][j-1] == 1:
            relations.append(seq(i+1,j-1))
        if i+1 < N and matrix[i+1][j] == 1:
            relations.append(seq(i+1,j))
        if i+1 < N and j+1 < M  and matrix[i+1][j+1] == 1:
            relations.append(seq(i+1,j+1))
        graph[seq(i,j)] = relations

vis = [0 for i in range(0,N*M)]

def dfs(i):
    vis[i] = 1
    stack = []
    for item in graph[i]:
        stack.append(item)
    while len(stack) > 0:
        id = stack.pop()
        if vis[id] == 1:
            continue
        vis[id] = 1
        for item in graph[id]:
            stack.append(item)
count = 0
for i in range(0,N*M):
    if vis[i] == 1 or matrix[i//M][i%M] == 0:
        continue
    count += 1
    dfs(i)

print(count)

其中，dfs 使用的是栈来实现