【知识点】 ---线段树的常用操作

1.什么是线段树？

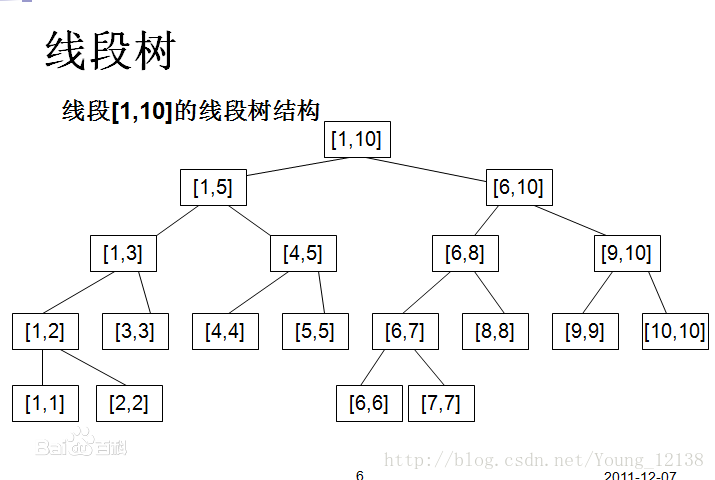
• 线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

• 性质：对于线段树中的每一个非叶子节点[a,b]，它的左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树，最后的子节点数目为N，即整个线段区间的长度。

• 举例说明：
  

2.构造线段树

• 成员声明：

struct node
{
    int l, r;
    int sum;
} tree[MAX<<2];

• 建树思想：递归建树，遇到叶子节点直接赋值，否则递归左右建树，回溯即可。

void build(int l, int r, int rt)
{
    tree[rt].l = l;
    tree[rt].r = r;
    tree[rt].sum = 0;
    if(l == r) //叶子结点
    {
        scanf("%d",&tree[rt].sum);
        return ;
    }
    int mid = (l+r)>>1;
    //递归建树
    build(l, mid, rt<<1);
    build(mid+1, r, rt<<1|1);
    pushup(rt);
}

3.更新线段树(单点)

• 更新思路：递归更新，递归至要更新的叶子节点，回溯更改该叶子节点。

void update(int pos, int val, int rt)
{
    //更新这个区间的值
    if(tree[rt].l == tree[rt].r)
    {
        tree[rt].sum += val;
        return ;
    }
    int mid = (tree[rt].l+tree[rt].r)>>1;
    if(pos <= mid)
        update(pos, val, rt<<1);
    else
        update(pos, val, rt<<1|1);
    pushup(rt);
}

4.区间查询

• 查询思路：

(1).区间求和

void query(int x, int y, int rt)
{
    if(x == tree[rt].l && y == tree[rt].r)
    {
        ans += tree[rt].sum;
        return ;
    }
    int mid = (tree[rt].l+tree[rt].r)>>1;
    if(y <= mid)
        query(x, y, rt<<1);
    else if(x > mid)
        query(x, y, rt<<1|1);
    else
    {
        query(x, mid, rt<<1);
        query(mid+1, y, rt<<1|1);
    }
}

(2).区间最大值

void qMax(int x, int y, int rt)
{
    if(tree[rt].l == x && tree[rt].r == y)
    {
        ans1 = max(ans1, tree[rt].Max);
        return ;
    }
    int mid = (tree[rt].l+tree[rt].r)>>1;
    if(y <= mid)
        qMax(x, y, rt<<1);
    else if(x > mid)
        qMax(x, y, rt<<1|1);
    else
    {
        qMax(x, mid, rt<<1);
        qMax(mid+1, y, rt<<1|1);
    }
}

(3).区间最小值

void qMin(int x, int y, int rt)
{
    if(tree[rt].l == x && tree[rt].r == y)
    {
        ans2 = min(ans2, tree[rt].Min);
        return ;
    }
    int mid = (tree[rt].l+tree[rt].r)>>1;
    if(y <= mid)
        qMin(x, y, rt<<1);
    else if(x > mid)
        qMin(x, y, rt<<1|1);
    else
    {
        qMin(x, mid, rt<<1);
        qMin(mid+1, y, rt<<1|1);
    }
}

5.更新线段树(区间)

• 区间更新是指更新某个区间内的叶子节点的值，因为涉及到的叶子节点不止一个，而叶子节点会影响其相应的非叶父节点，那么回溯需要更新的非叶子节点也会有很多，如果一次性更新完，操作的时间复杂度肯定不是O(lgn)，例如当我们要更新区间[0,3]内的叶子节点时，需要更新出了叶子节点3,9外的所有其他节点。为此引入了线段树中的延迟标记概念，这也是线段树的精华所在。

• 每个节点新增加一个标记，记录这个节点是否进行了某种修改(这种修改操作会影响其子节点)，对于任意区间的修改，我们先按照区间查询的方式将其划分成线段树中的节点，然后修改这些节点的信息，并给这些节点标记上代表这种修改操作的标记。在修改和查询的时候，如果我们到了一个节点p，并且决定考虑其子节点，那么我们就要看节点p是否被标记，如果有，就要按照标记修改其子节点的信息，并且给子节点都标上相同的标记，同时消掉节点p的标记。

(1).延迟操作的实现：

void pushdown(int rt) //延迟操作，更新当前结点的叶子
{
    int len = tree[rt].r - tree[rt].l + 1;
    tree[rt<<1].sum += tree[rt].lazy*(len-len/2);
    tree[rt<<1|1].sum += tree[rt].lazy*(len/2);
    tree[rt<<1].lazy += tree[rt].lazy;
    tree[rt<<1|1].lazy += tree[rt].lazy;
    tree[rt].lazy = 0;
}

(2).更新时的实现：

void update(int x, int y, long long val, int rt)
{
    //更新这个区间的值
    if(tree[rt].l == x && tree[rt].r == y)
    {

        tree[rt].lazy += val;
        tree[rt].sum += (y-x+1)*val;

        return ;
    }

    if(tree[rt].lazy)
        pushdown(rt);  //向下更新枝叶的值

    int mid = (tree[rt].l+tree[rt].r)>>1;
    if(y <= mid)
        update(x, y, val, rt<<1);
    else if(x > mid)
        update(x, y, val, rt<<1|1);
    else
    {
        update(x, mid, val, rt<<1);
        update(mid+1, y, val, rt<<1|1);
    }
    pushup(rt);
}

(3).查询时的实现：

long long query(int x, int y, int rt)
{
    if(tree[rt].l == x && tree[rt].r == y)
        return tree[rt].sum;

    if(tree[rt].lazy)
        pushdown(rt);  //向下更新枝叶的值

    int mid = (tree[rt].l+tree[rt].r)>>1;
    if(y <= mid)
        return query(x, y, rt<<1);
    else if(x > mid)
        return query(x, y, rt<<1|1);
    else
        return query(x, mid, rt<<1) + query(mid+1, y, rt<<1|1);
}

说明：

• 建树时的成员变量根据题目要求自行增添即可，对应的pushup也是一样，一般情况下的pushup：

void pushup(int rt)
{
    tree[rt].sum = tree[rt<<1].sum + tree[rt<<1|1].sum;
    //tree[rt].Max = max(tree[rt<<1].Max, tree[rt<<1|1].Max);
    //tree[rt].Min = min(tree[rt<<1].Min, tree[rt<<1|1].Min);
}

• 虽说以上为线段树的常用操作，但是线段树的功能不仅仅是这些。就我做过的题目而言，还有在建树的成员中添加flag标记，表示下次是否还需更新以及更新的优先级等等。要想灵活运用线段树，还需继续深入学习呐。